软工作业3:结对项目
一、软工作业3:结对项目:四则运算
| 软件工程 | 21计科34班 |
|---|---|
| 作业要求 | 结对项目 |
| 作业目标 | 结对设计实现一个生成四则运算题目的命令行程序 |
| 作业GitHub地址 | https://github.com/Gustavo3121005172/3121005172.git |
| 结对同学 | 库迪热提·热合曼3121005172 谭伟涛(外院同学) |
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
40 |
40 |
|
· Estimate |
· 估计这个任务需要多少时间 |
40 |
40 |
|
Development |
开发 |
780 |
520 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
100 |
60 |
|
· Design Spec |
· 生成设计文档 |
60 |
40 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
50 |
30 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
30 |
30 |
|
· Design |
· 具体设计 |
120 |
60 |
|
· Coding |
· 具体编码 |
300 |
200 |
|
· Code Review |
· 代码复审 |
60 |
60 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
60 |
60 |
|
Reporting |
报告 |
210 |
150 |
|
· Test Report |
· 测试报告 |
60 |
60 |
|
· Size Measurement |
· 计算工作量 |
30 |
30 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
120 |
60 |
|
合计 |
|
1030 |
710 |
3.1改进思路
1.数值存储原本与运算符共同存储为同一数组中,后续发现在分割中难辨别字符类型。随后根据除法的特殊性改变数据类型为Num类。
2.尽量处理好包装类型和基本类型两者的使用场所。在TreeNode节点类中设置Num类,(string)symbol与Num类平级。
3.尽量避免不必要的创建,new新建变量应在函数调用完毕即可释放空间。
4.括号的处理进行改进。toStringArray...函数中需要对随机生成的外括号去除。但是最初操作单纯是对字符串首尾进行简单的判定。后续发现双括号运算式按照此操作去除外括号后,导致二叉树插入括号造成运行失败。
5.慎用异常,创建异常开销较大。针对不同情况应特殊讨论。
6.待改进:通过空格分割得到中缀表达式二叉树和后缀表达式使用了split。split由于支持正则表达式,所以效率比较低。
3.2性能分析图
3.2.1生成题目功能及其覆盖率图
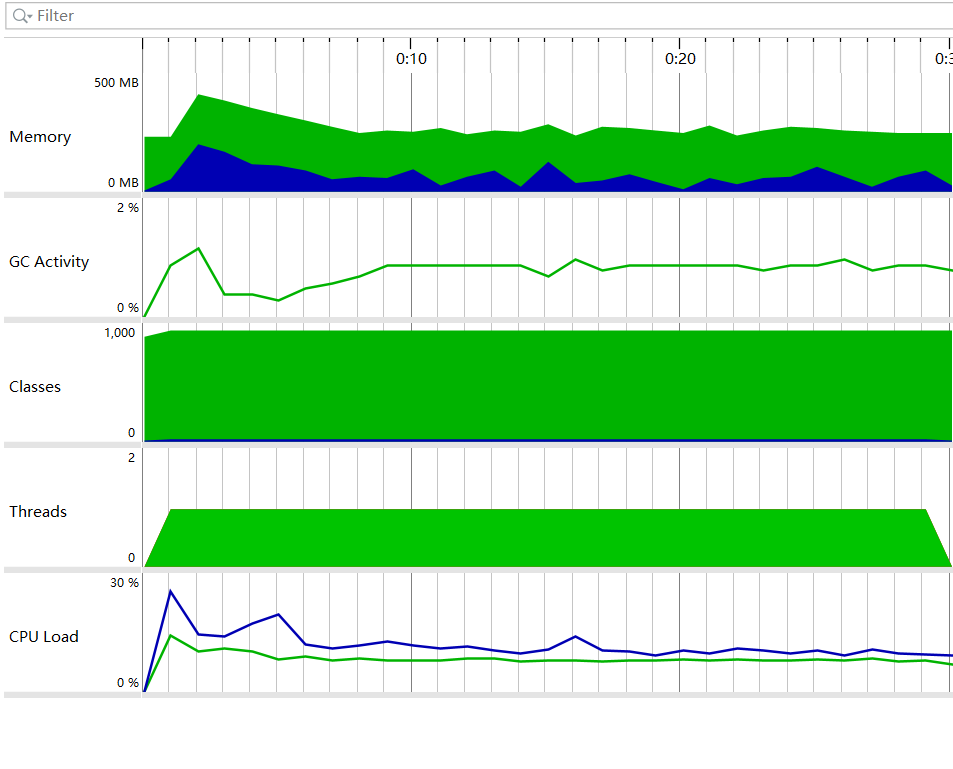
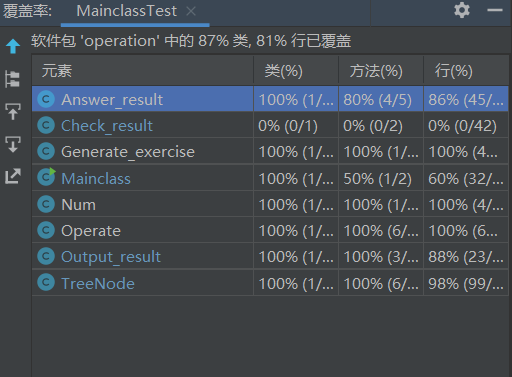
3.2.2检测对错覆盖率图
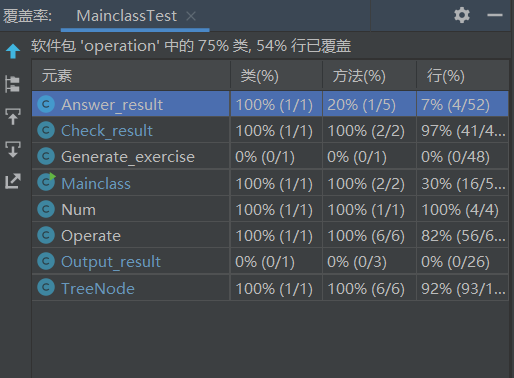
2.3函数消耗
生成题目功能函数消耗:
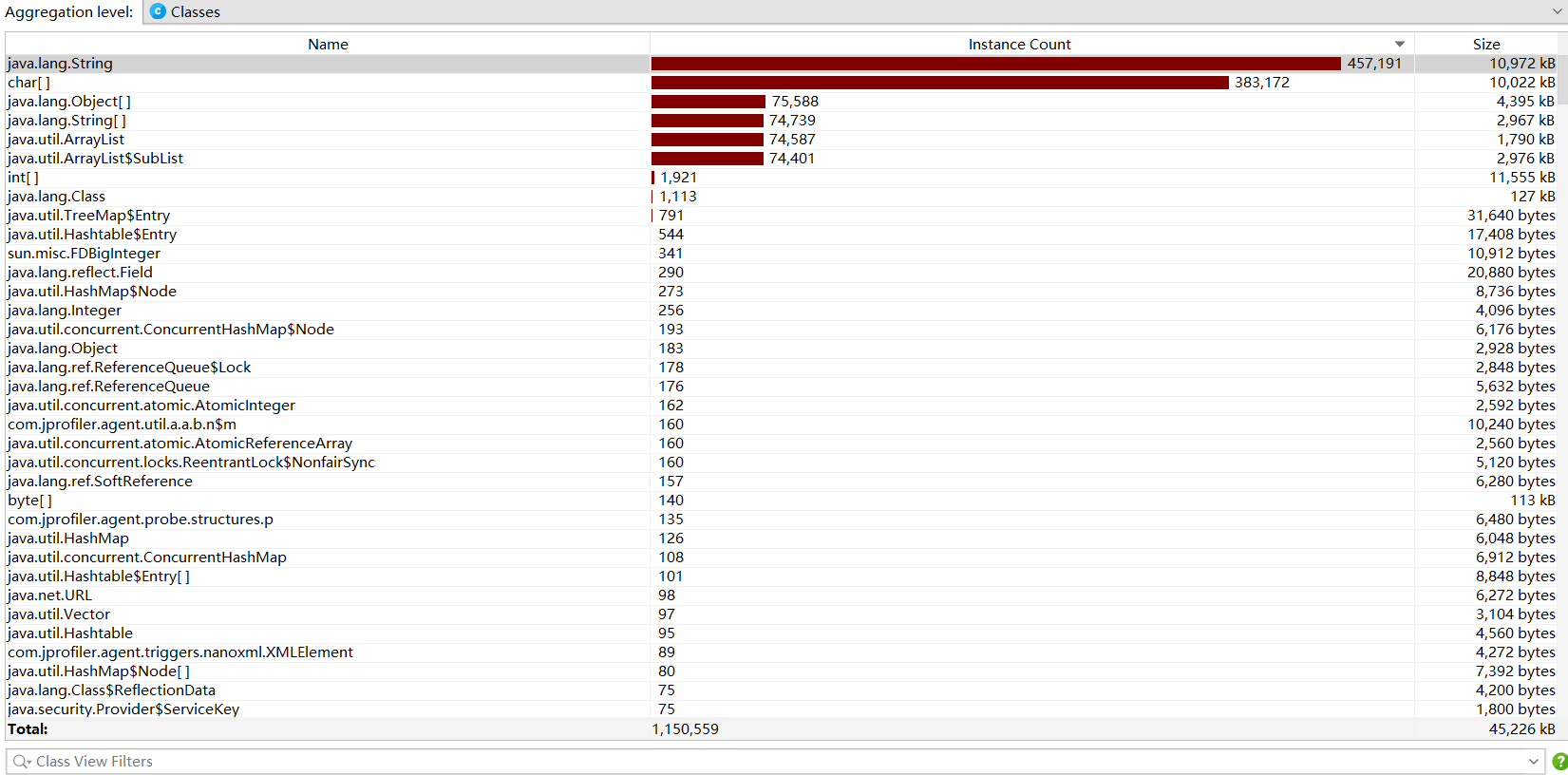
检测对错功能函数消耗:
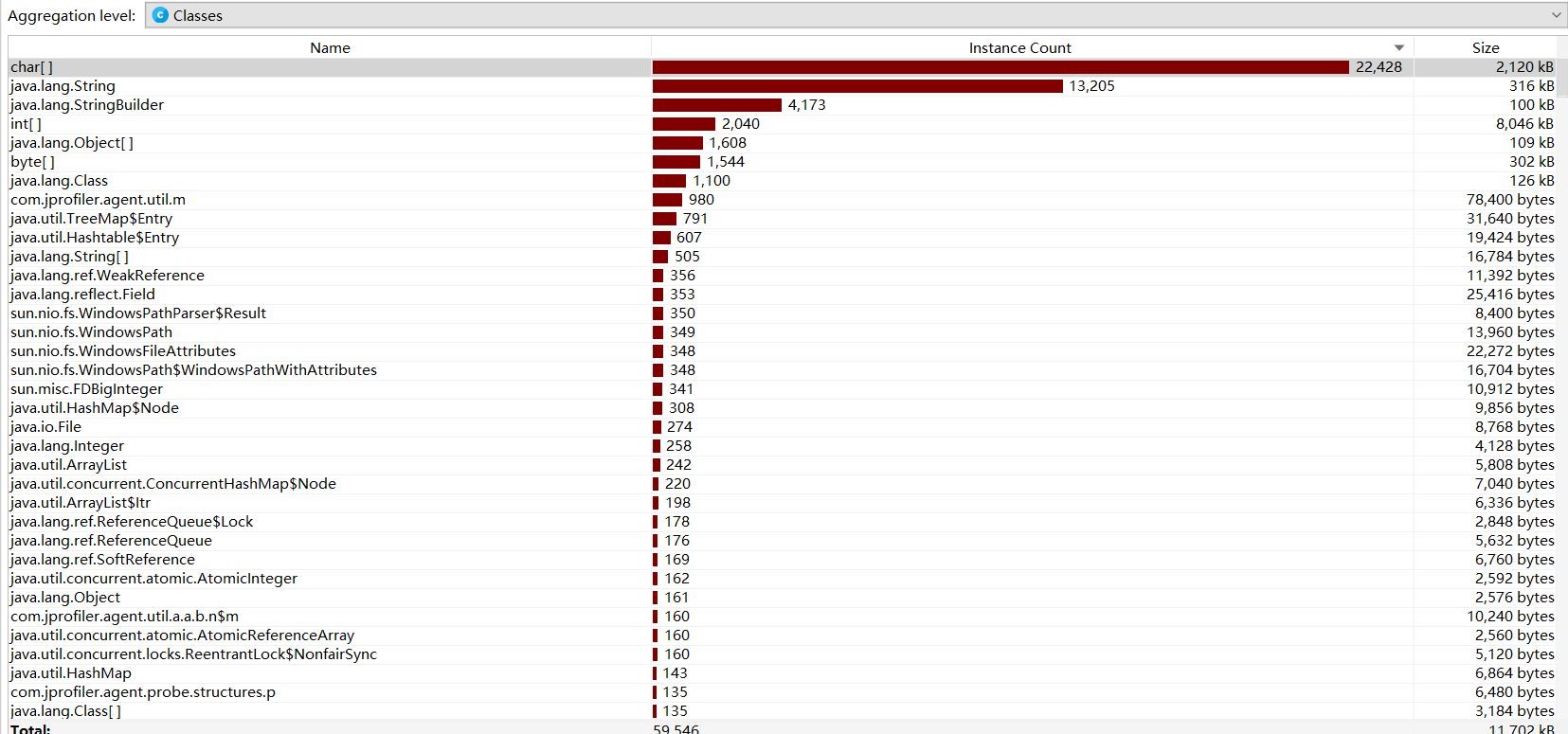
消耗最大的函数:String类型的函数。因为生成、转换、匹配和输出中缀表达式,和生成、处理、匹配查重表达式等操作消耗开销较大。
四、设计实现过程
4.1
主函数main函数:通过命令行获取参数,并运行参数对应的程序。
如下
1.获取参数"-n -r"执行生成题目和答案程序时:
执行过程:调用Generate_exercise类进行生成题目。通过循环执行:单题目的生成,后通过二叉树数据结构TreeNode类进行计算操作得到答案结果。针对各类情况对答案进行处理。如果满足程序要求,将该回答加入到查重列表(用于题目查重的数据结构)调用Output_result类进行输出题目和答案到文件中。
2.获取参数"-e -a"执行指定文件问答检查程序时:
执行过程:调用Check_result类进行检查,并将对错结果输出到指定文件中。
3.获取错误参数
返回参数输入错误信息。
4.2
generate函数:输入一个界定数范围,生成一个题目,返回一个题目字符串。
4.3
TreeNode函数:处理中缀表达式中的括号,并将表达式以二叉树结构呈现。
toStringArrayTrimOutParrenthes函数:去除表达式中最外层括号。
hasOperation函数:检测字符串中有无运算符。
isOperation函数:字符是否为运算符。
calculate函数:调用operate函数的四则运算,通过左右子树递归方式得到结果。
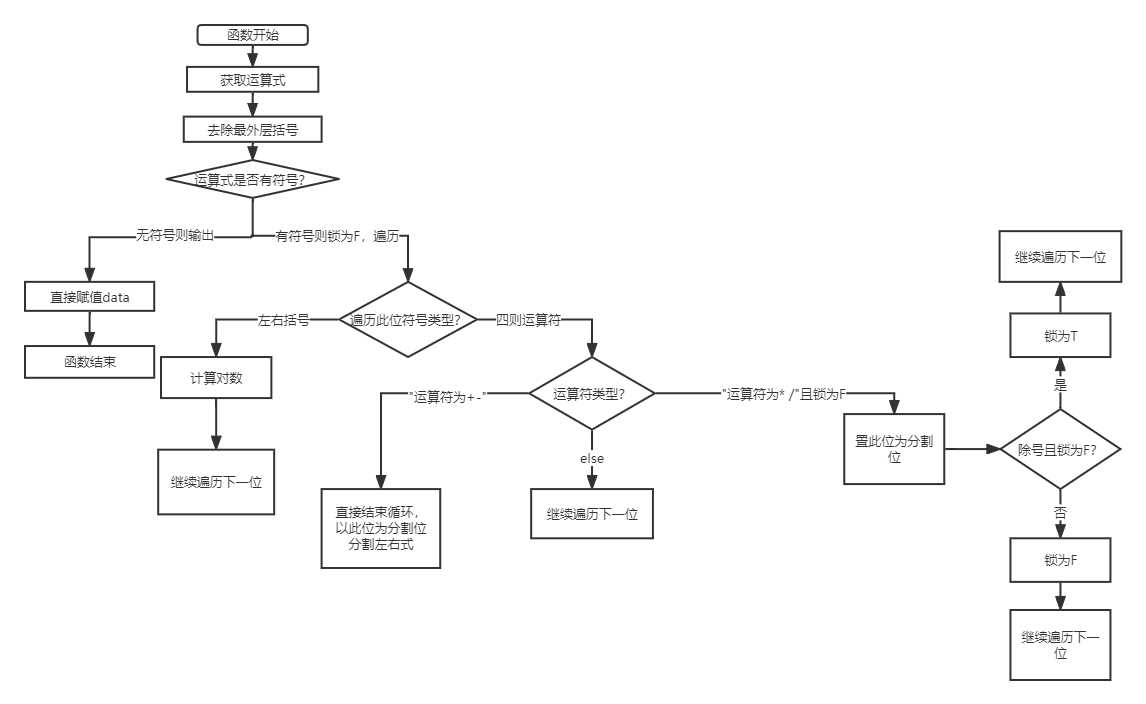
4.4
answer函数:传入题目,解出Num类型的答案,及分数字符串。
toPostifixExp函数:将中缀表达式转化为后缀表达式。
getDupExpression函数:将后缀表达式转化为查重表达式。
IsRepeat函数:检测查重列表里的表达式是否与新的表达式是否重复。
4.5
plus加法函数
subtract减法函数
multiple乘法函数
divide除法函数
simplify化简函数
4.6
output函数:每次输出在原先的基础上添加式子,并输出题目文件和答案文件。
clearInfoForFile函数:对文件进行清空,方便执行下一次程序。
dupCheck函数:对比两个查重表达式是否重复
4.7
check函数:输入题目文件和答案文件,调用回答问题函数判断答案是否正确,输出得分文件
五、代码说明
5.1以二叉树的结构
解释说明:
将式子存入字符串数组中,然后带入消除外层括号函数(消除括号,例如(1 * 2 / ( ( 3 + 4 ) * ( - 5+ 6 ) ))的最外层括号,主要用于消除分支节点中的括号,例如( 3 + 4 )),然后从右向左扫描每一个元素,找到最外层(括号外的)中最左边的符号,将该符号(例如式子中的*)作为父节点,将符号两边的式子作为子节点。
例如:
1 * 2/ ( ( 3 + 4 ) * ( 5 + 6 ) )
然后递归计算这两个子节点,也就是作为表达式再次代入。
右式 2 / ( ( 3 + 4 ) * ( - 5 + 6 ) )的计算结果是:
___/___
___2___ ___(( 3 + 4 ) * ( - 5 + 6 ) )___
于是目前的结果就是:
___*___
___1___ ___/___
2 ( 3 + 4 ) * ( - 5 + 6 )
类推,得到运算式二叉树。
当遍历运算符为+或者-时,直接以此运算符位作为分割左右式(index位)。左右式继续递归(消除外层括号函数生效)。左右式又是新的运算式。
由于* 号左右式交换不影响结果,但/号左右可以看作是是分子和分母。举例:

由于从右向左遍历寻找最左边的运算符,程序会默认分割成以下二叉树:
___+___
___2___ ___/___
___4___ ___9 / 22___
导致实际后除号没有被识别到,而右式作为被除数参与前除号运算。
于是提出当遍历运算符为*或/,且优先级锁为false,分割标志位为当前位。当匹配的是除号且优先级锁为false,将优先级锁上锁。即避免类似双除号运算,后除号失去优先级的情况。优先分割优先级高的运算符。
故结果应为
___+___
___2___ ___/___
___/___ ___22___
___4___ ___9___

关键代码:
public TreeNode(String[] exc)
{
exc=TreeNode.toStringArrayTrimOutParrenthes(exc);//对最外层括号进行去除,以找到最左运算符
if (exc == null) {
return;
}//空值情况
int length = exc.length;//去括号后的中缀表达式字符串
int index = 0;//分割标志位
if (hasOperation(exc)) {//此式中含有运算符
boolean lock=false;//定义优先级锁且置为未锁
int parenthes = 0;//括号对数
for (int i = length - 1; i >= 0; i--) {//从右向左推进查找
if (exc[i].equals("(")) {
parenthes--;//匹配左括号,左右括号成对
} else if (exc[i].equals(")")) {
parenthes++;//匹配右括号,右括号增加
}
if (parenthes > 0) {
continue;//右括号仍然未匹配成对,继续遍历
}
if (exc[i].equals("*") || exc[i].equals("/")&&lock==false) {
index = i;//当匹配*或者/时,且优先级锁为false,分割标志位为当前位
if(exc[i].equals("/")&&lock==false)//当匹配的是除号且优先级锁为false,将优先级锁上锁
lock=true;//
} else if (exc[i].equals("+") || exc[i].equals("-")) {
index = i; //一旦匹配+或者-时,立即结束for语句
break;
}
}
if (isOperation(exc[index])) {
symbol = exc[index]; //当标志位的字符是运算符而不是括号时,置Num类的运算符类型为当前位的符号
isSymbol=true;//本位置是运算符
}
String[] sbleft = new String[index];//定义 构建分割位左边的运算式
String[] sbright = new String[length-index-1];//定义 构建分割位右边的运算式
for (int i = 0; i < index; i++) {
sbleft[i]=exc[i];
}
for (int i = index + 1; i < length; i++) {
sbright[i-index-1] = exc[i];
}
//上述两个循环以分割位为原点,继续建立左运算式和右运算式
left = new TreeNode(sbleft);
right = new TreeNode(sbright);
//建立左子树和右子树
}else {//此式中不含有运算符,直接赋值,且本位置是数字
int data2=Integer.parseInt(exc[0]);
data=new Num(data2,1);
isSymbol=false;
}
}
5.2递归完成的计算答案
解释说明:
从根节点出发,进行后序遍历。叶子节点的左右子树为空,存放数字;根节点的左右子树不为空,存放运算符。通过匹配根节点存放的运算符进行左右子树的递归计算。
关键代码:
public Num calculate() {
Num result;//定义需要返回的答案
if (left == null && right == null) {
result = data;//当左子树为空且右子树为空,根节点聚集的答案为TreeNode节点的数字
} else {//左子树不为空或右子树不为空
Num leftResult = left.calculate();//左子树继续递归,计算左子树的结果
Num rightResult = right.calculate();//右子树继续递归,计算右子树的结果
if(symbol.equals("+"))
{
result =Operate.plus(leftResult,rightResult);//调用加法函数
}
else if(symbol.equals("-"))
{
result =Operate.subtract(leftResult,rightResult);//调用减法函数
}
else if(symbol.equals("*"))
{
result =Operate.multiple(leftResult,rightResult);//调用乘法函数
}
else if(symbol.equals("/"))
{
result =Operate.divide(leftResult,rightResult);//调用除法函数
}
else
return null;
}
return result;//每次递归一次函数就返回一个根节点聚集的答案
}
4.3使用饯
解释说明:
使用栈的入栈出栈,将后缀表达式表达为查重表达式。对比查重表达式是否重复,若不重复,存入列表中,用于后续运算式的查重。
关键代码:
public static String getDupExpression(String postfix){//后缀表达式转化为查重表达式
String dup=new String();
String[] s=postfix.split(" ");//以空格分割后缀表达式并返回字符数组
Pattern p = Pattern.compile("^-?\\d+$");//定的正则表达式编译为模式
Stack stack = new Stack();//新建存储栈
for(int i=0;i<s.length;i++)//字符从左到右遍历
{
if(p.matcher(s[i]).matches())//如果是数字
{
stack.push(s[i]);//出栈
}
else//如果是符号
{
String result= "#",num1,num2;
dup=dup+s[i];
dup=dup+" ";//空格用于后续分割
num1=stack.pop().toString();//入栈
num2=stack.pop().toString();
if(num1 != "#") {
dup=dup+num1;
dup=dup+" ";
}else{
}
if(num2 != "#") {
dup=dup+num2;
dup=dup+" ";
}else{
}
stack.push(result);
}
}
return dup;
}
public static boolean IsRepeat(List<String> exercises, TreeNode tree)//列表里的表达式是否与新的表达式是否重复
{
String exercise=Answer_result.toPostifixExp(tree);
exercise=Answer_result.getDupExpression(exercise);
for(int i=0;i< exercises.size();i++)
{
if(dupCheck(exercises.get(i),exercise))
return true;
}
return false;
}
public static boolean dupCheck(String str1,String str2) {//对比两个查重表达式是否重复
String[] s1=str1.split(" ");//将字符串s1转化成字符数组
String[] s2=str1.split(" ");//将字符串s2转化成字符数组
if(s1.equals(s2))
return true;//若两列表内容相同返回true
for(int j = 0; j < s2.length-1; j++) {//若不同进行循环将+或×后的两个字符串交换看能否相同
if(s2[j].equals("+")||s2[j].equals("×")) {
String temp= s2[j+1];
s2[j+1]=s2[j+2];
s2[j+2]=temp;
}
j*=3;
if(s1.equals(s2))
return true;//若交换后相同则返回true
}return false;
}
六、测试运行
6.1命令行参数 -n 100 -r 20
测试目的:用于实现正确参数生成题目和答案,并输出到指定文件
测试结果:生成100道题目,且生成数范围为20以内,且答案正确
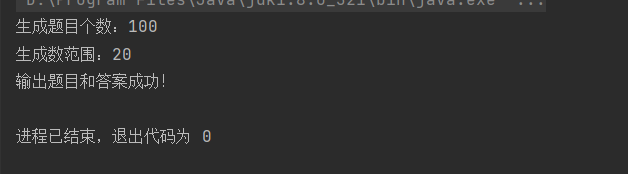
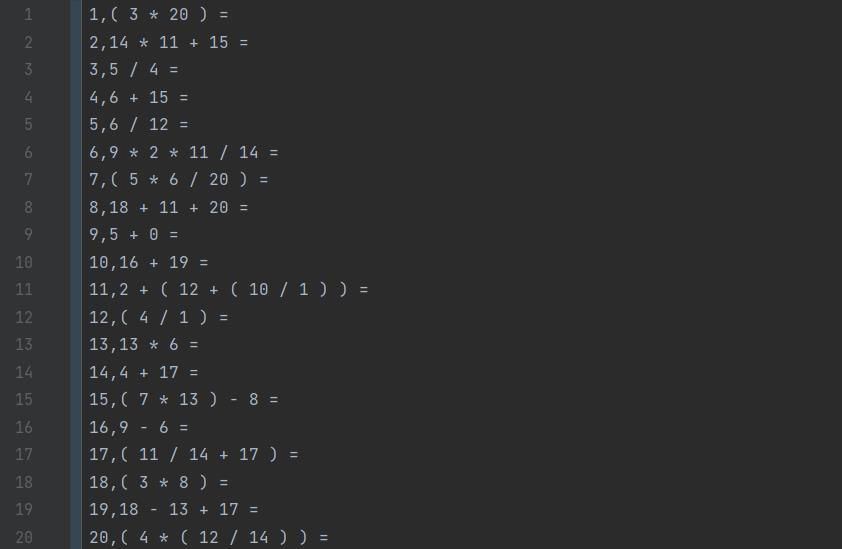
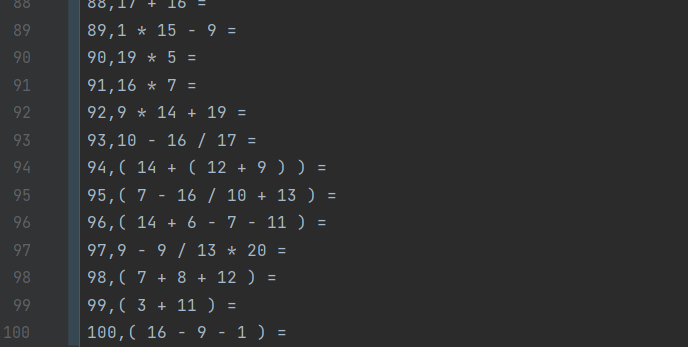
答案匹配:
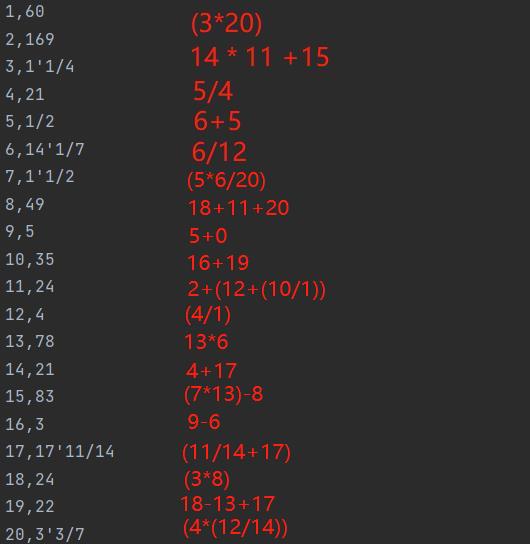
6.2命令行参数 -n 1000 -r 20
测试目的:用于实现正确参数生成题目和答案,并输出到指定文件
测试结果:生成1000道题目,且生成数范围为20以内,且答案正确
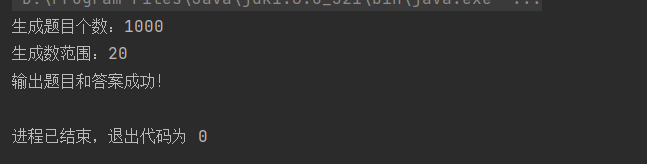
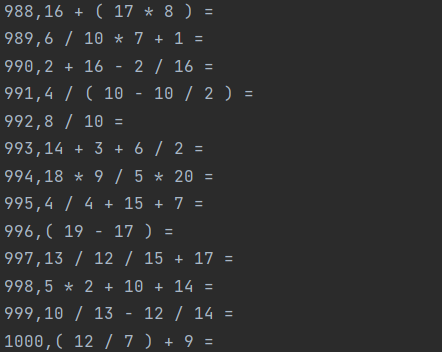
答案匹配
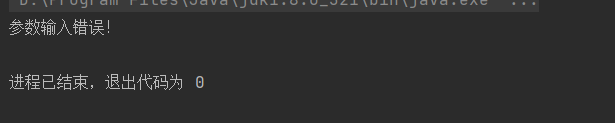
6.3命令行参数 @@ 100 -r 20
测试目的用于实现错误问题参数给出提示
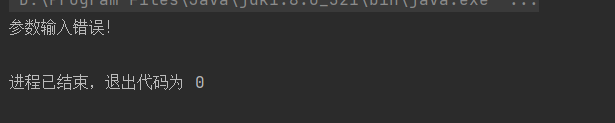
6.4命令行参数 -n 100 %% 20
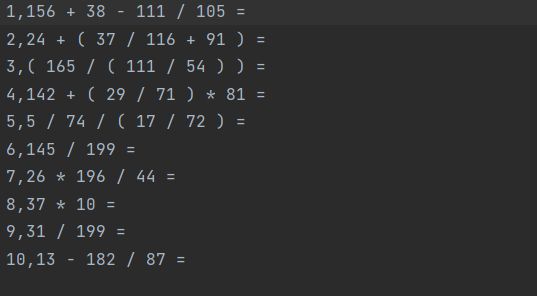
6.5-e src\resourse\testexercise1.txt -a src\resourse\testanswer1.txt
给定文件如下
testexercise1.txt:
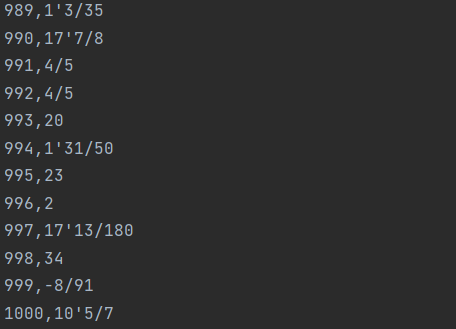
testanswer1.txt:

结果:

6.6-e src\resourse\testexercise2.txt -a src\resourse\testanswer2.txt
给定文件如下
testexercise2.txt:
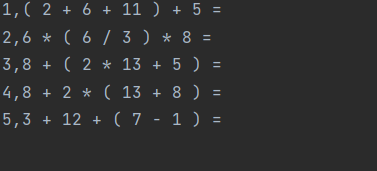
testanswer2.txt:
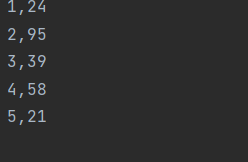
结果:
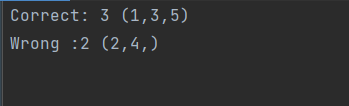
与设置顺序一样,五道题设置奇数序号为错误题
七、总结
多亏伟涛大佬有许多项目经验,帮我答疑了许多JAVA上的困扰,我们首先针对题目查重较复杂的情况,伟涛提出先将中缀表达式转化成后缀表达式,再用栈的结构处理查重表达式因为存在分数,
基本类型使用会出现以下情况:(1)使用整类型导致整除精确度损失(2)使用浮点类型导致后续运算得不到分数形式。处理方法:将分数的分子和分母分别以整型存储在Num类,将整数化为以分子为当前值,分母为一的Num类数据
项目在最初只实现一小部分需求,在考虑个人编程能力和完成程度进一步增添需求,并且针对每种情况修改程序代码。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号