10-04 矩形覆盖（斐波那契数列的应用）

题目描述： 

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

 

解题思路与代码：

1） 排列组合：

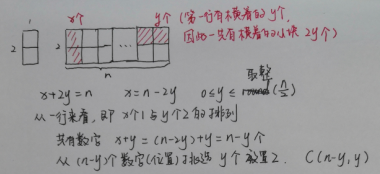
class Solution {
public:
    int rectCover(int number) {
        if(number<=0) return 0; //没有，会报错。因为f(0)=1.(也进入了循环)
        int count = 0;
        for(int two = 0;two<= (number/2);two ++){ //two(y)：每行横着放置的小块数目
            count += com(number-two,two);
        }
        return count;
    }
    
    int com(int m,int n){  //计算C(n-y,y)
        int i = m; 
        int sum=1;
        for(int j = 0;j < n;j++,i--){
            sum = sum *i / (j+1);        // m/1    (m-1)/2    (m-2)/3   ...   (m-n+1)/n
        }
        return sum;
    }
};

2）当n>2时，用第一个2*1的小矩形去覆盖大矩形的最左侧，有两种选择，竖着放或者横着放。

竖着放时，右边还剩下2*(n-1)的区域，覆盖的方法同f(n-1)相同。

横着放时，其下面也必须横着放，此时右边还剩下2*(n-2)的区域，覆盖方法同(n-2)相同。

n<=0，f(n)=0；

n=1，f(1)=1；

n=2，f(2)=2;

class Solution {
public:
    int rectCover(int number) {
        if(number<=0)return 0;
        if(number==1)return 1;
        if(number==2)return 2;
        long long numRes = 2;
        long long temp = 1;
        for(int i = 3;i<=number;i++){
            numRes = numRes + temp;
            temp = numRes - temp;
        }
        return numRes;
    }
};