平衡二叉树(AVL树)& LeetCode1382将二叉搜索树变平衡
1.二叉排序树的时候,树的结构是非常依赖无序序列的顺序,这样会出现极端的情况。
在最好的情况下,二叉排序树的查找效率比较高,是O(logn),其访问性能近似于折半查找
最差的情况是O(n),比如插入的元素是有序的,生成的二叉排序树就是一个链表,这种情况下,需要遍历全部元素才行。
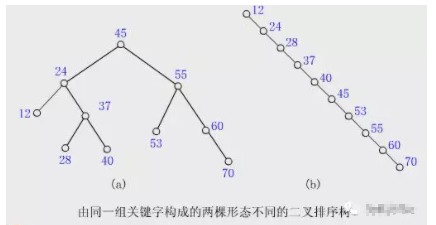
【如图1】:
这样的一颗二叉排序树就是一颗比较极端的情况。我们在查找时候,效率依赖树的高度,所以不希望这样极端情况出现,而是希望元素比较均匀的分布在根节点两端。
2.什么是二叉平衡树?
问题提出:
能不能有一种方法,使得我们的二叉排序树不依赖无序序列的顺序,也能使得我们得到的二叉排序树是比较均匀的分布。
引入:
平衡二叉树(Self-Balancing Binary Search Tree 或 Height-Balanced Binary Search Tree),是一种特殊的二叉排序树,其中每一个结点的左子树和右子树的高度差至多等于1.
这里的平衡从名字中可以看出,Height-Balanced是高度平衡。
它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1.(|h(L)-h(R)| <= 1)
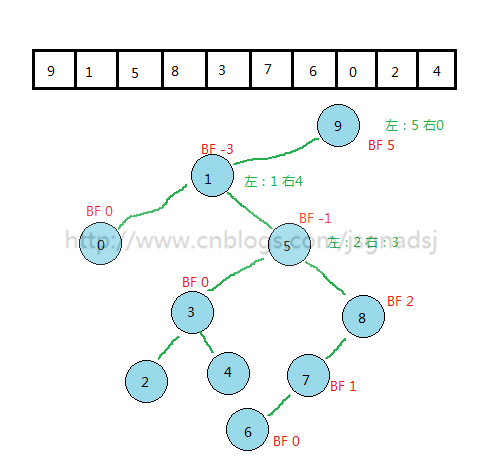
若将二叉树上的结点的平衡因子BF(Balance Factor)定义为该节点的左子树的深度减去它的右子树的深度,则平衡二叉树上所有结点的平衡因子只可能是-1、0、1。否则就不是平衡二叉树。
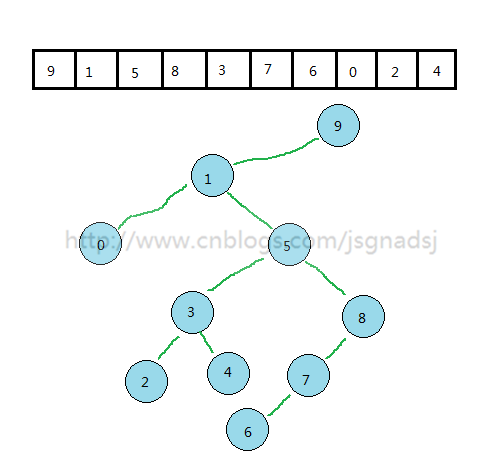
上图图1中,就不是平衡二叉树。
以图1来看看各个结点的平衡因子。
【如下图2】:
插入数据,会破坏树的平衡性,要做单旋或双旋
当插入的数据在树的外侧的时候,需要单旋
当插入的数据在树的内侧的时候,需要双旋
如何构成平衡二叉树?
(1)当最小不平衡树的根结点的平衡因子BF是大于1时,就右旋
(2)当最小不平衡树的根结点的平衡因子BF是小于1时,就左旋
(3)插入结点后,最小不平衡子树的BF与它的子树的BF符号相反时,就需要对结点先进行一次旋转以使得符号相同后,再反向旋转一次才能够完成平衡操作。

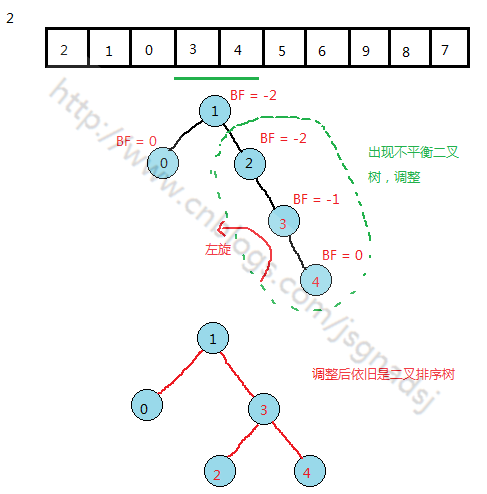
要能找到最小不平衡树,4是插入结点,与2结点平衡因子绝对值大于1

注意此处的结点2的变化


注意9结点的位置出现了BF=1,与它的子树BF相反
leetcode题
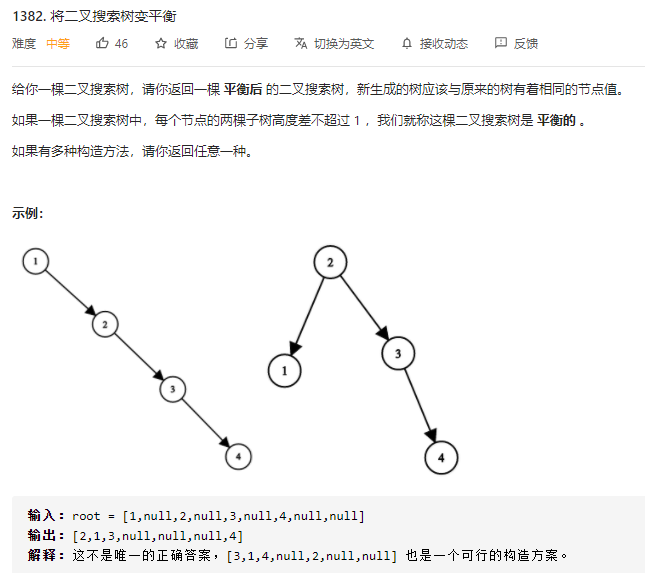
思路:可以中序遍历把二叉树转变为有序数组,然后在根据有序数组构造平衡二叉搜索树。
二叉排序树的中序遍历一定是从小到大的。
Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def balanceBST(self, root: TreeNode) -> TreeNode:
if not root:
return None
res = []
self.inOrder(root, res)
return self.buildTree(res, 0, len(res)-1)
# 中序遍历构造有序数组,中序遍历得到的就是从小到大排序好的数组
def inOrder(self, root, res):
if not root:
return []
if root.left:
self.inOrder(root.left, res)
res.append(root)
if root.right:
self.inOrder(root.right, res)
# 有序数组构造平衡二叉树
def buildTree(self, res, l_idx, r_idx):
mid_idx = (l_idx + r_idx) // 2
mid_point = res[mid_idx]
mid_point.left = None
mid_point.right = None
if l_idx < mid_idx:
mid_point.left = self.buildTree(res, l_idx, mid_idx-1)
if r_idx > mid_idx:
mid_point.right = self.buildTree(res, mid_idx+1, r_idx)
return mid_point
JAVA
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode balanceBST(TreeNode root) {
if (root == null) return null;
// vals用来存放节点
List<Integer> vals = new ArrayList<>();
inOrder(root, vals);
return buildTree(vals, 0, vals.size()-1);
}
private void inOrder(TreeNode x, List<Integer> vals) {
if(x == null) return;
inOrder(x.left, vals);
vals.add(x.val);
inOrder(x.right, vals);
}
private TreeNode buildTree(List<Integer> vals, int lo, int hi) {
if(lo > hi) return null;
if(lo == hi) return new TreeNode(vals.get(hi));
int mid = (hi - lo) / 2 + lo;
TreeNode x = new TreeNode(vals.get(mid));
x.left = buildTree(vals, lo, mid-1);
x.right = buildTree(vals, mid+1, hi);
return x;
}
}
参考文档:
http://blog.sina.com.cn/s/blog_66770c8501015xmw.html
http://www.eefocus.com/xiaols/blog/13-12/300934_f5e45.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号