Lingo求解不等式 函数最大值遇到的问题 | 不等式变量取值错误问题 | @bnd()问题 （@bnd();结果与x>1;x<7;结果不一样?）

首先，提出第一个问题，

1.当目标函数与约束条件不相关时候，即：目标函数中没有约束条件的变量时：变量如何取值？

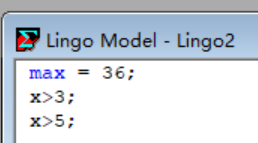
进行简单实验：（实验1）

 

 

 

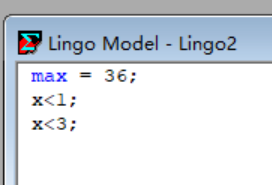
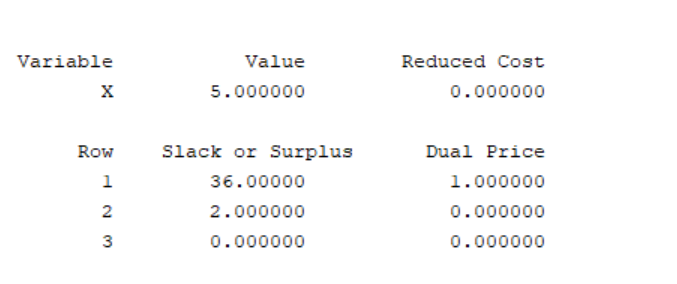
 结果为：

 

 

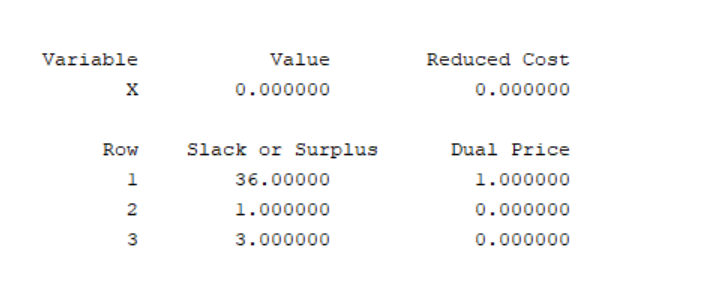
 此时的变量取到0；

我们对两个不等式的顺序进行互换：（实验2）

 

 

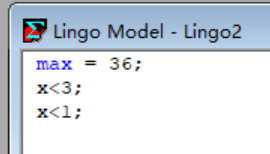
 结果为：

 

 

 因此得到第一个猜想1：不相关时，最终的取值与x的顺序有一定的关系

但是第一个结果的0为什么会出现呢？我的思路是判断x的默认范围：

 

 

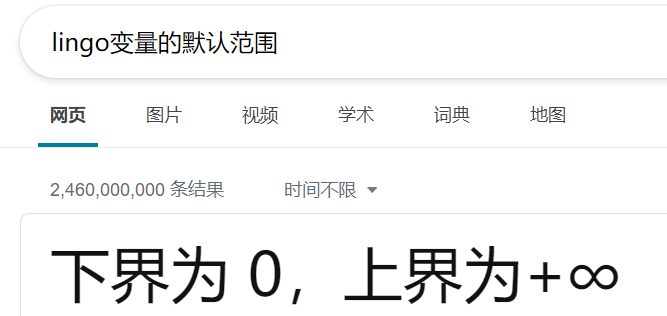
我们想到对变量执行@free(x);（实验3）

 

 

 

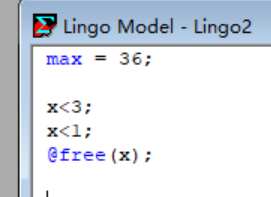
结果为：

 

 

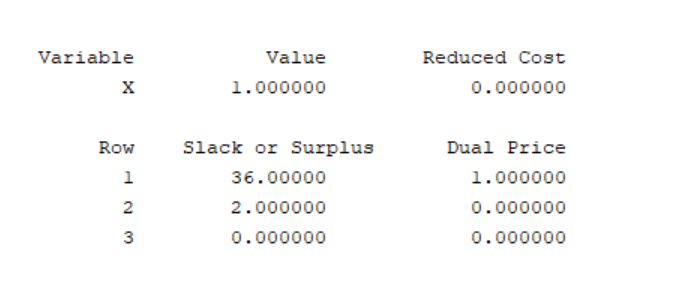
 再换顺序：（实验4）

 

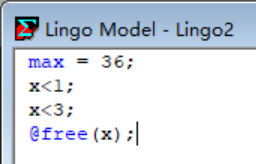
 结果符合约束交集：

 

 验证结果（实验4-1）:

 

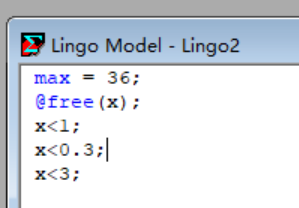
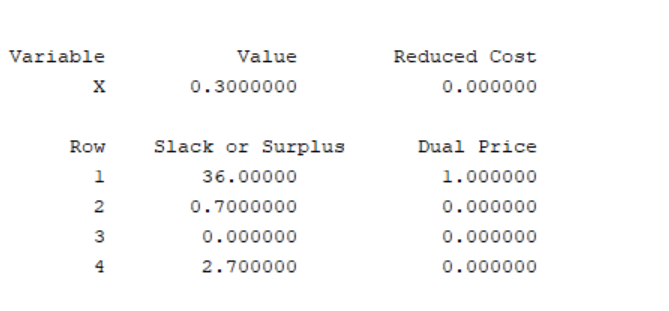
这里我们开始猜想2，约束与目标函数不相关，则约束不知道自己应该取最大值还是最小值（为方便理解，以下用区间表示）

使用@free后，取值都是x的右区间，假如右区间不存在呢？

实验5：

 

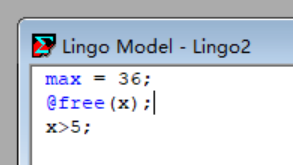
 则：右边界不存在，则取左边界

猜想3：左边界不存在，则取右边界

针对实验1的0，其实就是默认x的左边界，使用@free后，左边界不存在，则最后变成取右边界的数值；

实验1的特点是第一个式子比第二个式子的区间小，出现结果取左区间的现象

我们对另一种情况进行实验：

实验6-1：

 

 

 

 

 

 

 

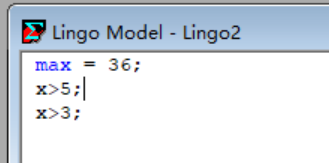
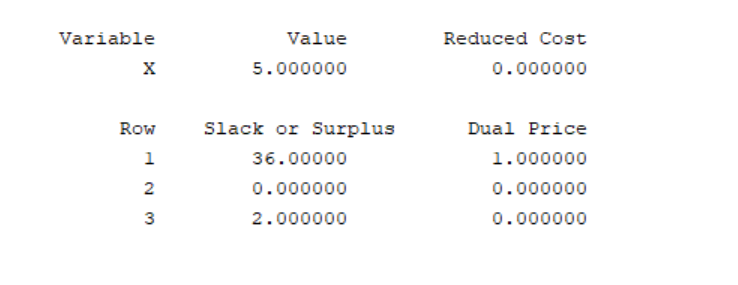
 实验6-2：（交换顺序，结果依然正确）

 

 

 

 

 

对于实验6-1，第一个区间比第二个区间小，取左边界，对于实验6-2，第一个区间比第二个区间大，取右边界，右边界没有，取左边界 

 

 

结论1：在目标函数与不等式约束不相关时，变量的取值不确定应该取最大还是最小。

 

结论2：当顺序执行时，第一个x的约束区间小于第二个x的约束区间时候，取左边界

对结果为0的现象使用@free()后，使得x的左边界的0消失，默认使用交集的右边界

 

结论3：如果右边界为无穷，则使用左边界。（实验1，5）

为什么探究这个问题？一般谁会这么写不相关的约束与目标呢？

当我们写目标函数的时候，可能出现一种情况：相关变量的系数为0，这种情况有时候不易被发现

当系数为0时候，就出现了我们上边的问题，此时我们仍然想知道，变量取何值时目标函数最大，因为系数为0可能只是一种情况

而我们需要得到一般情况下取最值时候变量的解

这时候得出的结果就会产生错误，也是>、<与@bnd的结果不一致的诱因，我们来看看实例：

 

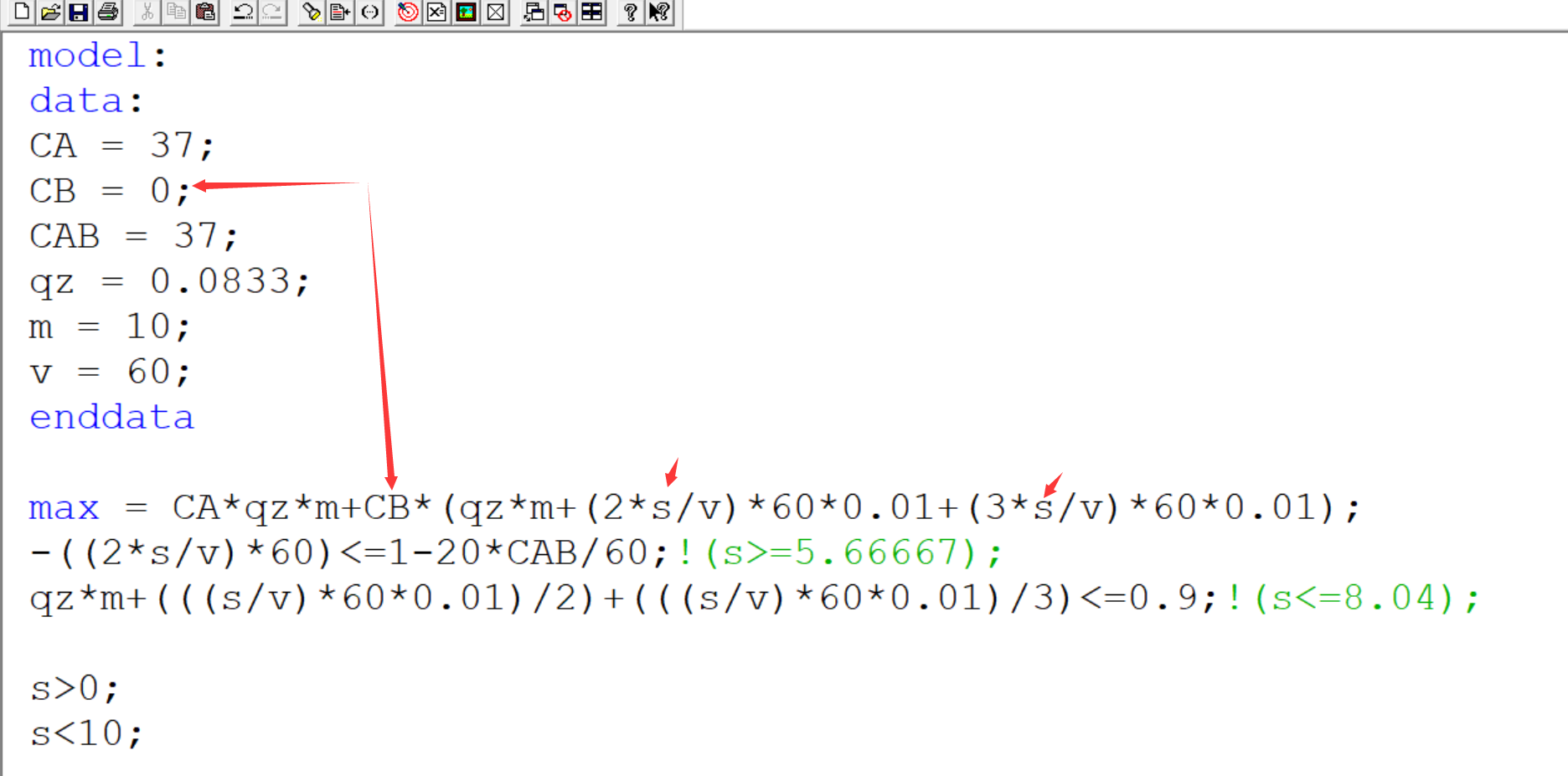
 此处，我们使用>、<进行约束，结果为：

 

 

 

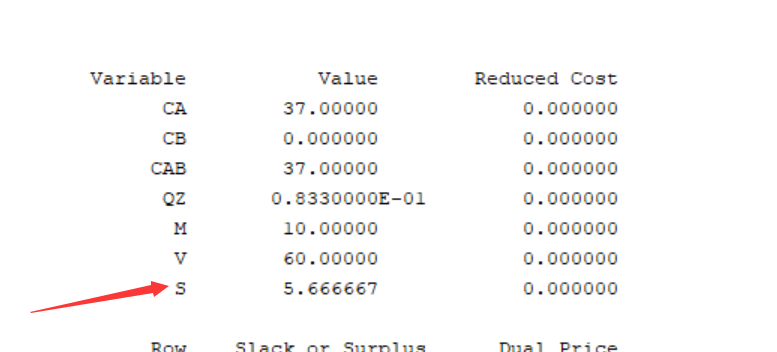
 我们修改使用@bnd进行计算：

 

 

 

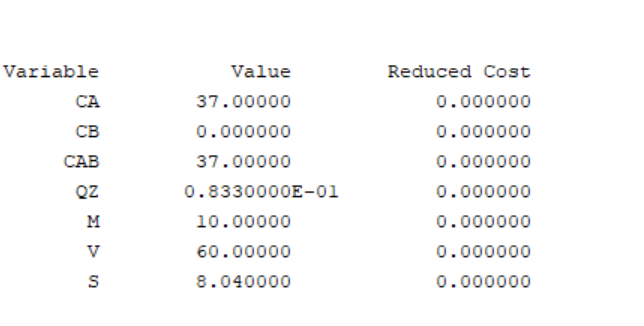
 结果为8.04

 

我们直接给出结论，使用第一个>、<进行约束时候，s>0的约束条件下s的区间是最大的

上面的s>5.6667,s<8.04均比s>0的区间小，因此结果取到交集的左边界，也就是5.66667，我们交换顺序，结果也是5.6667

而当我们使用函数@bnd的时候，@bnd没有给出s一个确定的区间，因此程序中只有两个不等式，s>=5.66667,与s<=8.04

此时我们交换两个式子的顺序，让小区间s<=8.04排到前面，发现结果发生变化：

 

 

 

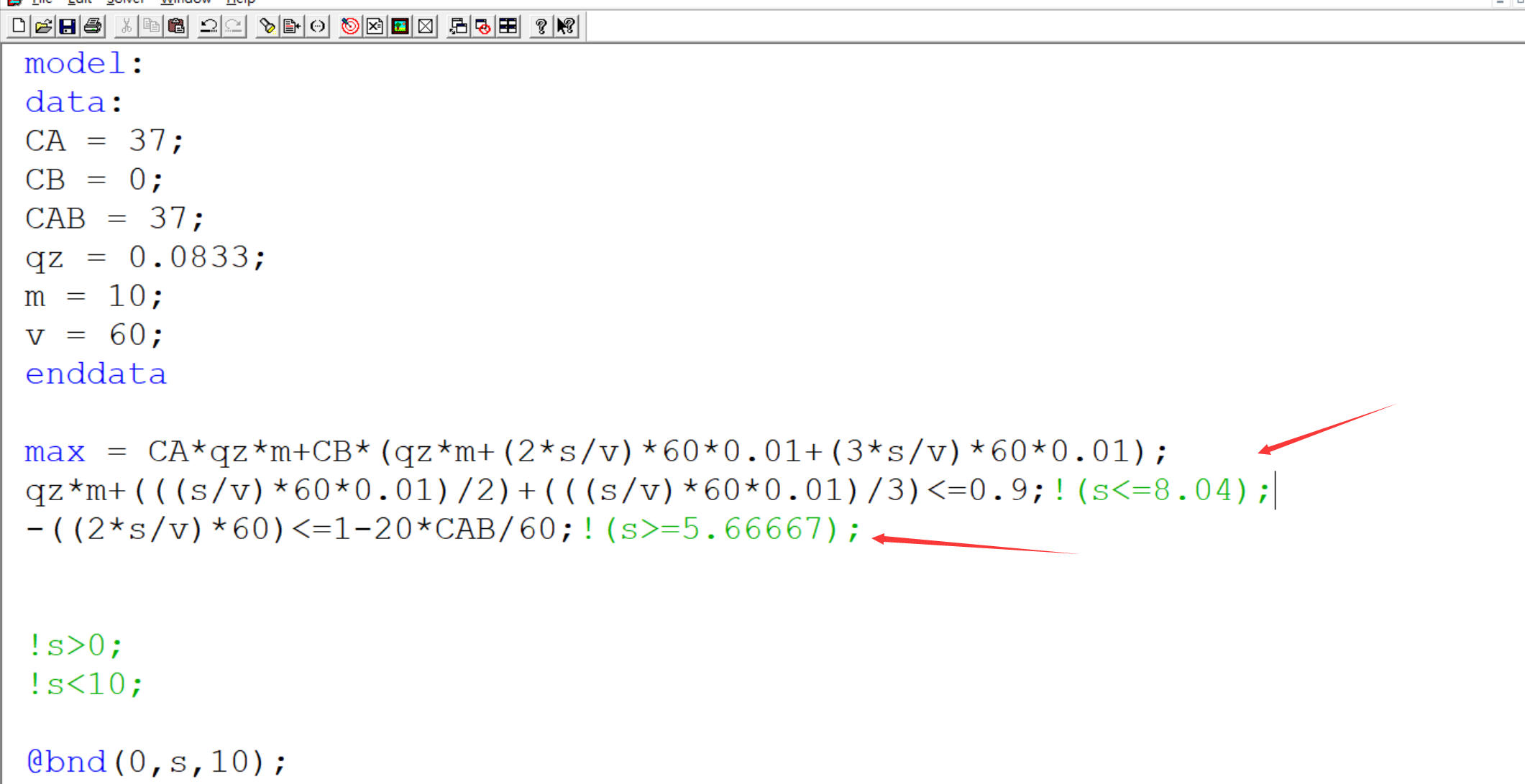
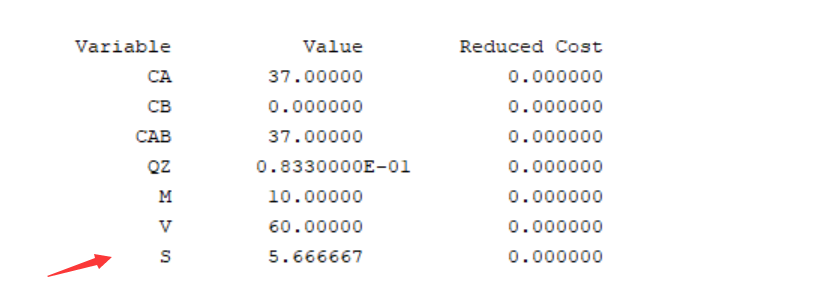
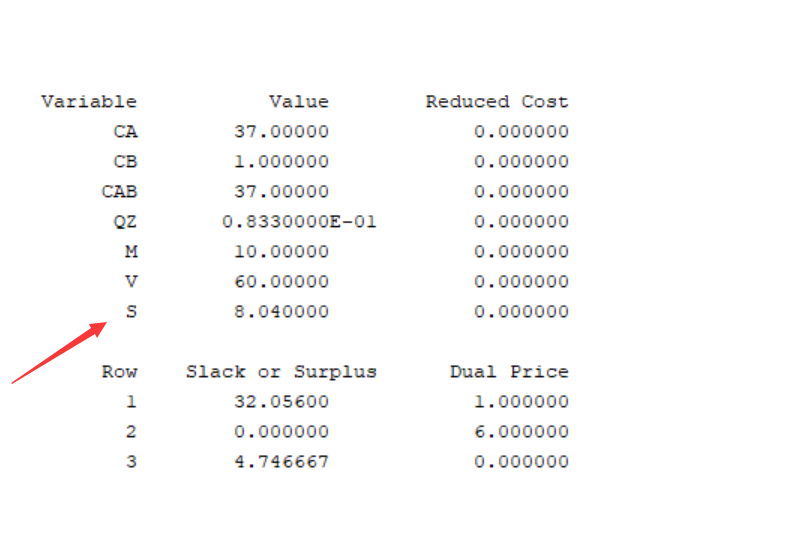
 说明我们的结论是可行的

 

解决方案：将系数CB改为一个不为0的数字，则变量重新明确自己的取值，结果便不会出错了