最长公共序列

题目：给定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
输入格式
第一行包含两个整数 N 和 M。

第二行包含一个长度为 N 的字符串，表示字符串 A。

第三行包含一个长度为 M 的字符串，表示字符串 B。

字符串均由小写字母构成。

输出格式
输出一个整数，表示最大长度。
数据范围
1≤N,M≤1000
输入样例：
4 5
acbd
abedc
输出样例：
3
思路：
**集合f[i][j]表示a的前i个字母，和b的前j个字母的最长公共子序列长度

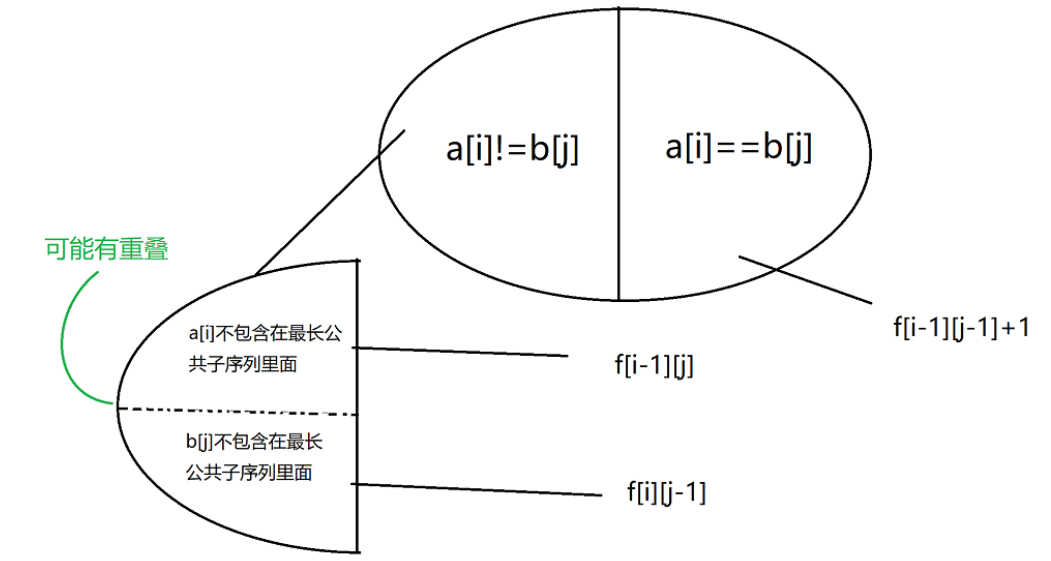
如果两个字符相等，可以直接继承到到f[i-1][j-1] + 1,只是在2前i-1,j-1基础上多加了一组，如果不相等，如图

我们需要继承之前的最大匹配数量，我们从f[i-1][j]和f[i][j-1]之间获取，主要看f[i-1][j]和f[i][j-1]的比较，因为a[i]和b[j]一定不相等了,但a[i]或者b[j]可能在之前出现了和它们相等的数使得
他们配对成功,那么我们转移配对成功的就是当前f[i][j]的最大情况的转移了,当然也有可能a[i],b[j]在此之前都没有
成功配对，总之就是从两种状态中挑取最大的配对数进行状态转移
code：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e3 + 10;

char a[N], b[N];

int f[N][N];

int main(){
    int n, m;
    cin >> n >> m >> a+ 1 >> b + 1;
    
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++){
            if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1] + 1;
            else f[i][j] = max(f[i - 1][j],f[i][j - 1]);
        }
    
    cout << f[n][m] << endl;
    return 0;
}