求组合数

组合数公式

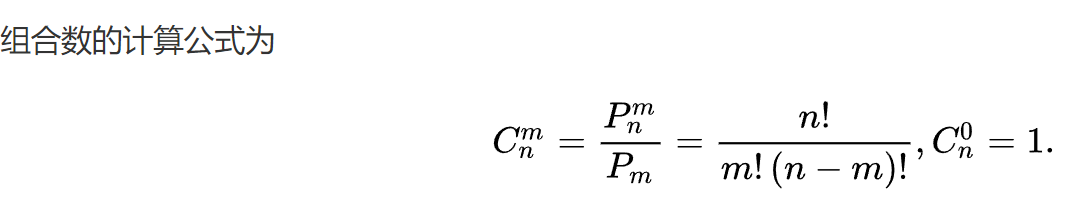
C(a,b) = C(a-1,b) + C(a-1,b-1)
对小数据范围直接套公式就可：
code:

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2008;

int a[N][N];

int e = 1e9 + 7;

void init(){
    for (int i = 0; i < 2008; i ++){
        for (int j = 0; j <= i; j ++ ){
            if (!j) a[i][j] = 1;
            else a[i][j] = (a[i - 1][j] + a[i -1][j -1])%e ;
        }
    }
}

int main(){
    init();
    int t;
    cin >> t;
    while (t --){
        int m, b;
        cin >> m >> b;
        cout << a[m][b] << endl;
    }
    return 0;
}

当范围扩大，我们使用费马小定理求乘法逆元，用快速幂求解
code:

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e5 +10,mod = 1e9 + 7;

ll fact[N],infact[N];

ll fast(ll a, ll b, ll c){
    ll ans = 1;
    a %= c;
    while (b){
        if (b % 2) ans = ans * a % c;
        b /= 2;
        a = a * a % c;
    }
    return ans;
}

int main(){
    fact[0] = infact[0] = 1;
    for (int i = 1; i <= N; i ++){
        fact[i] = fact[i-1] * i % mod;
        infact[i] = infact[i-1] * fast(i,mod - 2, mod) % mod;
    }
    ll n,a,b;
    cin >> n;
    while (n --){
        cin >> a >> b;
        cout << fact[a] * infact[a - b] % mod * infact[b] % mod << endl;
    }
    return 0;
}

Lucas定理实现：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long ll;

ll fast (ll a, ll k, ll p){
    int res = 1;
    while (k)
    {
        if (k & 1) res = (ll)res * a % p;
        a = (ll)a * a % p;
        k >>= 1;
    }
    return res;
}

ll C (ll a, ll b, ll p){
    
    if (a < b) return 0;
    
    ll ans = 1;
    for (ll i = 1, j = a; i <= b; i ++ , j --){
        ans = (ll)ans * j % p;
        ans =(ll)ans * fast(i,p-2,p) % p;
    }
    return ans;
}

ll lucas (ll a, ll b, ll p){
    ll ans = 1;
    if (a < p && b < p) return C(a,b,p);
    return C(a%p,b%p,p) * lucas(a/p,b/p,p) % p;
}

int main(){
    int t;
    cin >> t;
    while ( t--){
        ll a, b, p;
        cin >> a >> b >> p;
        cout << lucas (a , b, p) << endl;
    }
    return 0;
}