扩展欧几里得算法

裴蜀定理：若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。
它的一个重要推论是：a,b互质的充分必要条件是存在整数x,y使ax+by=1.
扩展欧几里得：
用于求解方程 ax+by=gcd(a,b) 的解

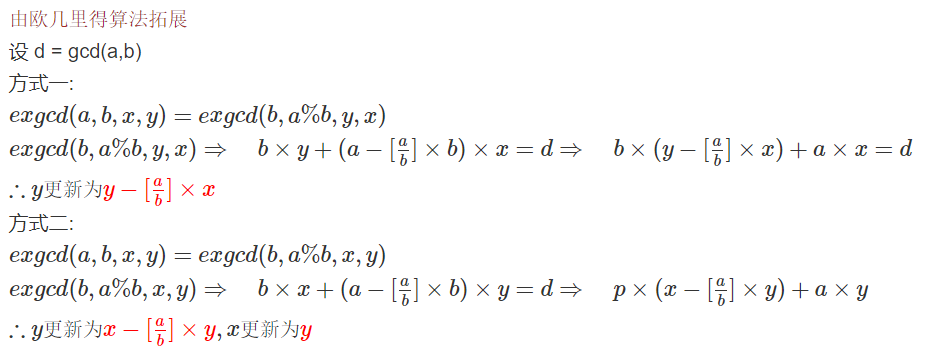
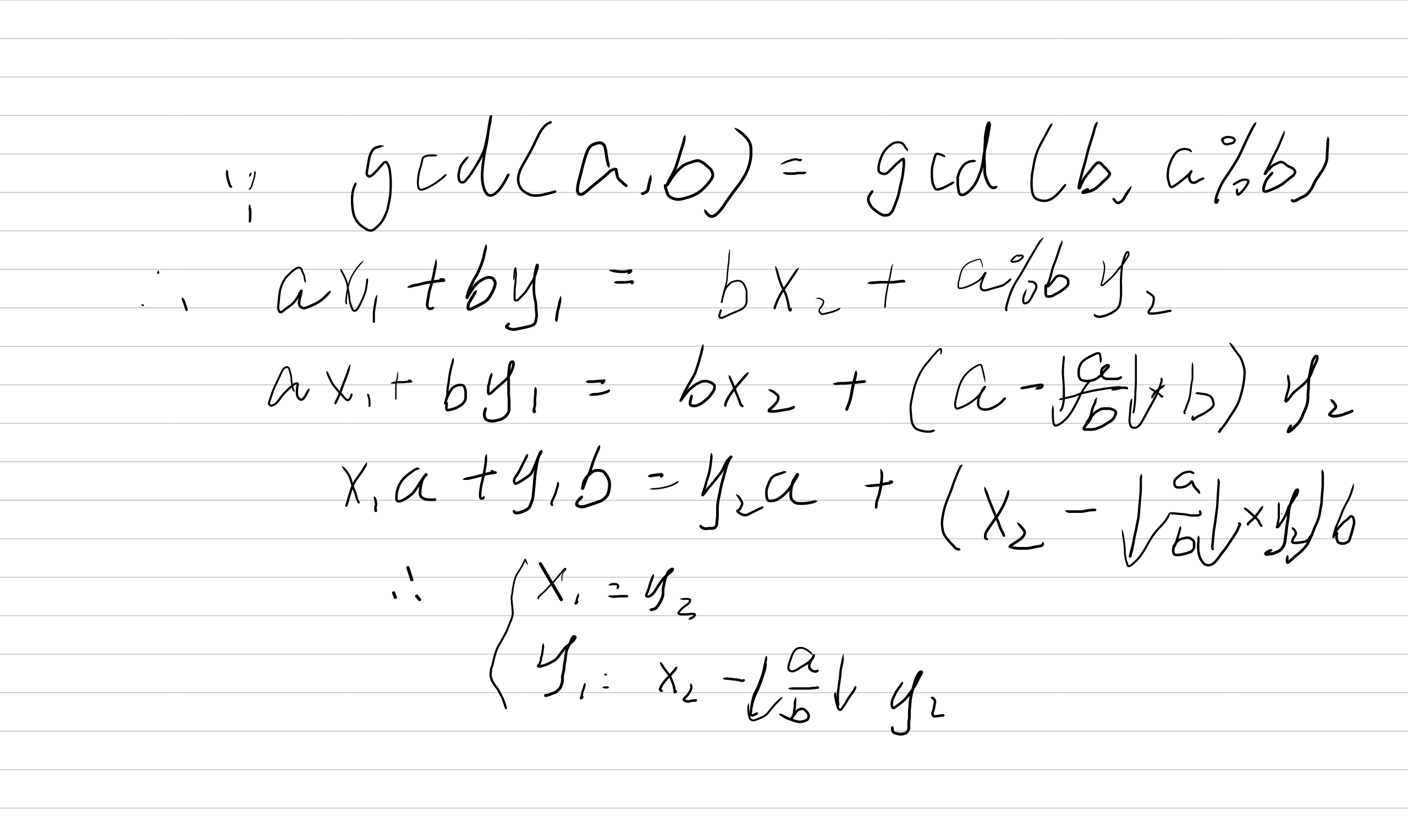
代码:

# include <bits/stdc++.h>

using namespace std;

void exgcd(int a , int b, int& x , int& y){
    if (!b){
        x = 1, y = 0;
        return;
    }
    exgcd(b,a%b,x,y);
    int t = y;
    y = x - a/b * y;
    x = t;
    
}

int main(){
    int n;
    scanf("%d",&n);
    while (n--){
        int a,b,x,y;
        scanf("%d%d",&a,&b);
        exgcd(a,b,x,y);
        printf("%d %d\n",x,y);
    }
    return 0;
}

习题：线性同余方程

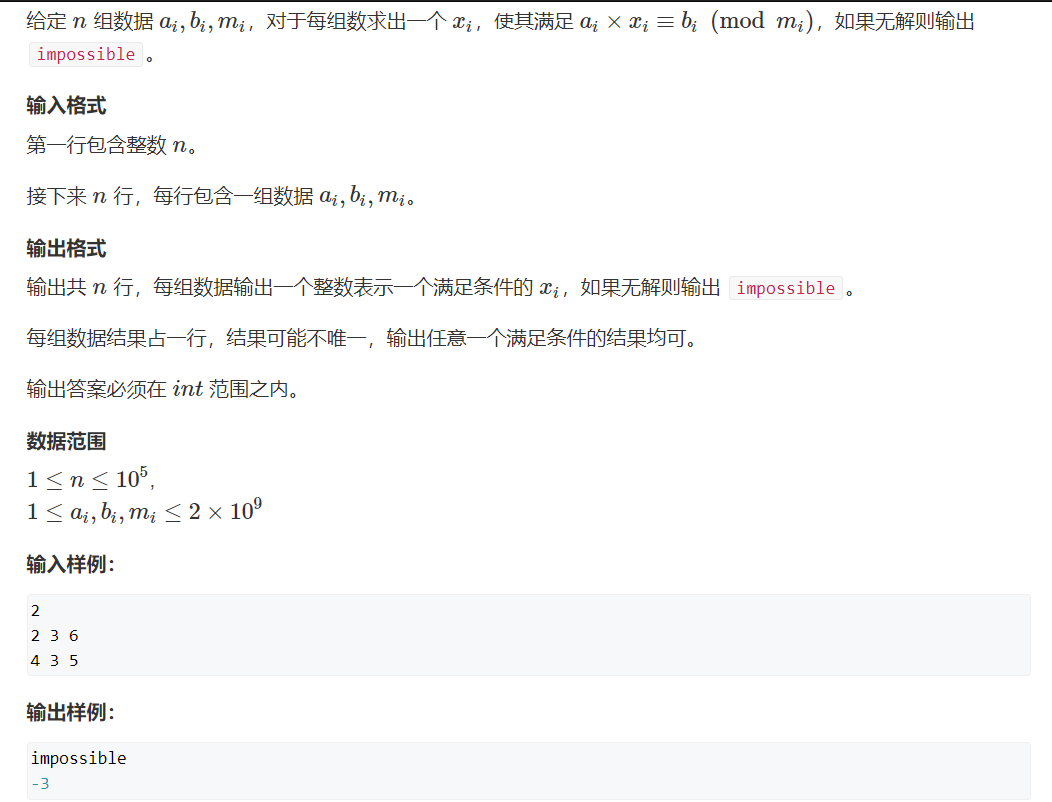
题解：求出一个x，使得ax % m = b， 也就是 ax + my = b, 对于gcd(a,m) = d, 我们知道ax + m*y = d 一定成立，那么 我们求aX + mY = b , 等式两边都乘以d/b,就是裴蜀定理，ax0 * b/d = ax ， x = x0 * b/d,要求在int范围，我们结果再mod m 就可
code：

# include <bits/stdc++.h>

using namespace std;

typedef long long LL;

int exgcd(int a, int b, int &x, int &y)  // 扩展欧几里得算法, 求x, y，使得ax + by = gcd(a, b)
{
    if (!b)
    {
        x = 1; y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= (a / b) * x;
    return d;
}

int main(){
    int n;
    scanf("%d",&n);
    while (n--){
      int a, b, m;
      int x, y;
      cin >> a >> b >> m;
      int d = exgcd(a,m,x,y);
      if (b%d) cout << "impossible" << endl;
      else {
          cout << (LL)x*(b/d) % m << endl;
      }
    }
    return 0;
}