线性筛理解及应用

目录
如何求出1~N的素数个数呢

朴素版筛法

我们只要将素数的倍数全部筛掉就可以
代码

埃氏筛
int isprime(int n){
    int cnt = 0;
	for (int i = 2; i <= n; i ++){
	    if (!st[i]) prime[cnt ++] = i;
        for (int j =  i; j <= n; j += i)
            st[j] = true;
	}

	return cnt;
}

线性筛法

埃氏筛法会将合数重复地筛掉，如有可以只筛一次合数，那么复杂度就会降到O(n)
线性筛（欧拉筛）就是通过合数最小的质因子筛掉这个合数

int isprime(int n){
    int cnt = 0 ;
    for (int i = 2; i <=n; i ++){
        if (!st[i]) prime[cnt++] = i;
        for (int j = 0; prime[j] <= n/i; j ++){
            st[prime[j] * i] = true;
            if (i%prime[j] == 0) break;
        }
    }
    return cnt;
}

线性筛的应用

求1~N的欧拉函数的和

欧拉函数

一个数n，那么1~n中和n互质的数的个数，就是n的欧拉函数
欧拉函数有以下性质：

线性筛法求欧拉函数

暴力写法直接求每个数的欧拉函数，再sum求和，复杂度接近n*n了

# include <iostream>

using namespace std;
typedef long long ll;
ll oula(int n){
    ll res = n;
    for (ll i = 2; i <= n/i;i ++ ){
        if (n%i == 0){
            while (n % i == 0) n/=i;
            res = res/i*(i - 1); 
        }
    }
    if (n > 1) res = res/n*(n-1);
    return res;
}

int main(){
    ll n;
    ll sum = 0;
    cin >> n;
    for (int i = 1; i <= n; i ++)
        sum += oula(i);
    cout << sum ;
    return 0;
    
}

下面是线性筛法，先看代码，再解释

# include <iostream>

using namespace std;

typedef long long ll;

const int N = 1e6 + 10;

bool st[N];  // 这里记录状态
ll prime[N]; // 存质数
ll phi[N];   // 欧拉函数

ll Euler(ll n){
    phi[1] = 1;
    int cnt = 0;
    for (int i = 2; i <= n; i ++){
        if (!st[i]){
            phi[i] = i - 1;
            prime[cnt ++] = i; 
        }
        for (int j = 0; prime[j] <= n/i; j ++){
            st[prime[j] * i] = true;
            if (i % prime[j] == 0){
                phi[i* prime[j]] = prime[j] * phi[i];
                break;
            }
            phi[i * prime[j]] = (prime[j] - 1) * phi[i];
        }
    }
    ll sum = 0;
    for (int i = 1; i <= n; i ++)
        sum += phi[i];
    return sum;
}

int main(){
    ll n;  
    cin >> n;
    cout << Euler(n);
    return 0;
}

6 可以是 23 ，那么 欧拉函数就是6（1-1/2）*（1-1/3），这里N是6， 而对于求2的100次方乘上 3的一百次方这样的数的楼拉函数，底数是不会改变的，我们 只需要更新N就可以

求phi[primes[j]i],分析phi[primes[j]i]和phi[i]的关系
如果i%primes[j]==0时,说明primes[j]为i的最小质因子,而phi[i]内已经乘过(primes[j]-1)/primes[j]
∴计算phi[primes[j]i]只需要更新N的值即可,即在phi[i]的基础上乘个primes[j]
∴phi[primes[j]i]=primes[j]phi[i];
如果i%primes[j]!=0时,primes[j]小于i的最小质因子,而phi[i]内没有乘过(primes[j]-1)/primes[j]
∴计算phi[primes[j]i]除了需要更新N值外,还需要乘上(primes[j]-1)/primes[j]
∴phi[primes[j]i]=primes[j]phi[i](primes[j]-1)/primes[j]=phi[i](primes[j]-1)
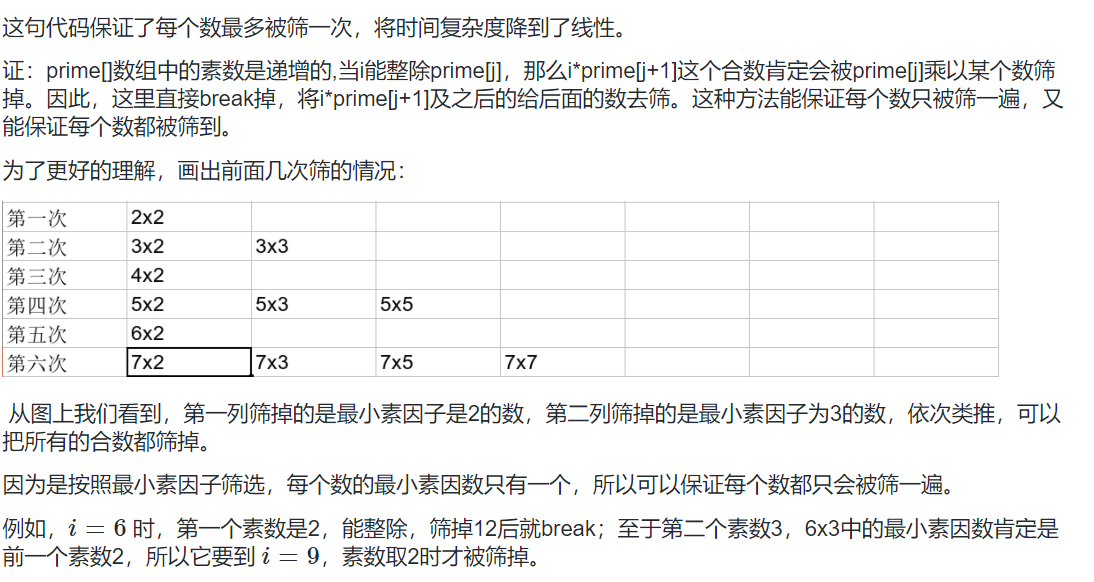
再看看大佬的表格促进理解：