树与图的BFS——图中点的层次
题意:给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 1,点的编号为 1∼n。
请你求出 1 号点到 n 号点的最短距离,如果从 1 号点无法走到 n 号点,输出 −1。
输入:第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 a 和 b,表示存在一条从 a 走到 b 的长度为 1 的边。
输出:输出一个整数,表示 1 号点到 n 号点的最短距离
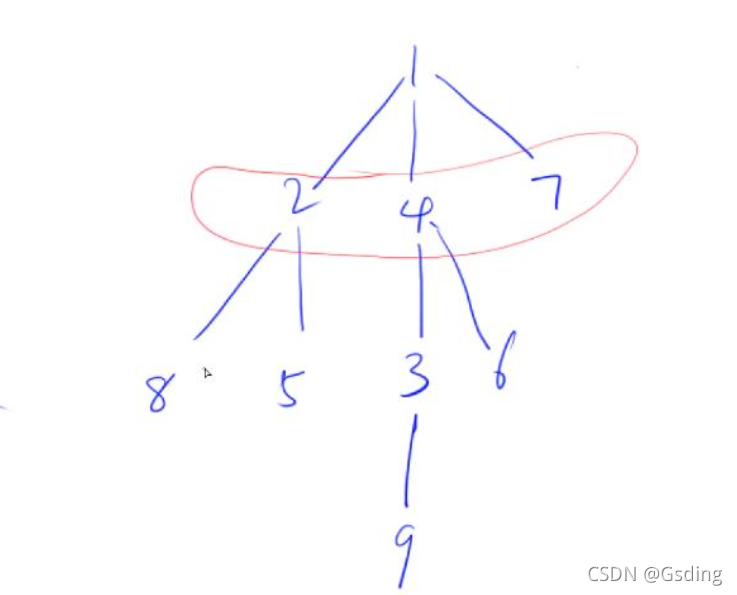

思路:层序遍历找出点和点的距离即可
模板 有向图的存储和bfs
int n, m, idx;
int h[N], ne[N], e[N];
int d[N];
void add (int a , int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++;
/* 就是把新建的边插入队头。(先把新建的边的next指向现在队头的next,
然后更新队头的next)*/
}
int bfs(){
queue<int> q;
q.push(1);
d[1] = 0;
while(q.size()){
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i]){
int j = e[i];
if (d[j] == -1){
d[j] = d[t] + 1;
q.push(j);
}
}
}
return d[n];
}
图中点的层次题解
# include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m, idx;
int h[N], ne[N], e[N];
int d[N];
void add (int a , int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++;
}
int bfs(){
queue<int> q;
q.push(1);
d[1] = 0;
while(q.size()){
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i]){
int j = e[i];
if (d[j] == -1){
d[j] = d[t] + 1;
if(j == n) break;
q.push(j);
}
}
}
return d[n];
}
int main(){
cin >> n >> m;
int a, b;
memset(d, -1, sizeof(d));
memset(h, -1, sizeof(h));
while (m --){
cin >> a >> b;
add(a, b);
}
cout << bfs();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号