pybind11(二):使用矩阵类演示 C++ 类的 Python 绑定方法
前面的文章主要介绍了如何在 Python 中调用简单的 C++ 函数,而本篇文章将进一步探讨如何在 Python 中使用 C++ 定义的类及其成员函数。本文将分别在 C++ 和 Python 中实现一个矩阵类,并为其编写矩阵乘法的成员函数。最后,我们将把两种实现与 NumPy 的矩阵乘法进行性能对比,以观察各自的效率差异。
矩阵类实现思路
定义一个矩阵需要三个基本要素:行数、列数以及存储矩阵元素的数据。对于矩阵操作,还需要一些基础方法,例如获取行数或列数,以及设置或读取指定位置的元素。因此,一个矩阵类可以定义如下:
# 矩阵类的伪代码
class Matrix:
int rows
int cols
vector<float> data
int get_row_num()
int get_col_num()
void set(int row, int col, float value)
float get(int row, int col)
在这个矩阵实现中,我们使用一维数组来存储矩阵的数据,并通过行列索引计算对应的一维下标,从而定位到具体的元素。
矩阵乘法实现思路
这里不使用任何矩阵乘法优化算法,就使用矩阵乘法定义的算法:
设矩阵 \(A\) 为 \(m \times n\),矩阵 \(B\) 为 \(n \times p\),则矩阵 \(C = A B\)为 \(m \times p\),其中元素 \(c_{ij}\) 的计算方式为:
# 计算 C = A × B 的伪代码
# A: m × n
# B: n × p
# C: m × p
for i = 0 to m-1:
for j = 0 to p-1:
C[i][j] = 0
for k = 0 to n-1:
C[i][j] += A[i][k] * B[k][j]
C++ 矩阵类具体实现
在明确了矩阵类的设计思路后,我们首先给出矩阵类在 C++ 中的完整实现。该实现包含数据存储、元素读写、随机填充、矩阵乘法等核心功能。
#include <cstddef>
#include <cstdlib>
#include <ctime>
#include <pybind11/pybind11.h>
class Matrix {
private:
int rows, cols;
std::vector<float> data;
public:
Matrix(int rows, int cols)
: rows(rows), cols(cols), data(rows * cols, 0.0f) {
srand((unsigned)time(NULL));
};
void set(int row, int col, float value);
float get(int row, int col) const;
int rows_num() const;
int cols_num() const;
// 使用随机数填充矩阵
void fill_random();
Matrix dot(const Matrix &other) const;
void print() const;
};
#include "matrix.h"
#include <cstdio>
#include <iostream>
#include <stdexcept>
void Matrix::set(int row, int col, float value) {
if ((row >= 0 && row < rows) && (col >= 0 && col < cols)) {
data[row * cols + col] = value;
}
return;
}
float Matrix::get(int row, int col) const {
float value;
if ((row >= 0 && row < rows) && (col >= 0 && col < cols)) {
value = data[row * cols + col];
}
return value;
}
int Matrix::rows_num() const { return rows; }
int Matrix::cols_num() const { return cols; }
void Matrix::fill_random() {
for (float &i : data) {
i = rand() / float(RAND_MAX);
}
}
Matrix Matrix::dot(const Matrix &other) const {
if (other.rows != cols) {
std::invalid_argument("Matrix dimisions not match for dot product!");
}
Matrix result(rows, other.cols);
float sum = 0;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < other.cols; j++) {
sum = 0;
for (int k = 0; k < cols; k++) {
sum += this->get(i, k) * other.get(k, j);
}
result.set(i, j, sum);
}
}
return result;
}
void Matrix::print() const{
std::cout << '[' << ' ';
for (int i = 0; i < rows_num(); i++) {
for (int j = 0; j < cols_num(); j++) {
std::cout << get(i, j) << " ";
}
if (i < rows_num() - 1)
std::cout << '\n' << " ";
}
std::cout << "]" << '\n';
return;
}
使用 pybind11 将 C++ 类导出
为了使 Python 能直接调用 C++ 实现的矩阵类,我们使用 pybind11 将其封装为 Python 扩展模块。通过绑定类的方法、构造函数以及成员函数,Python 端便可像使用普通对象一样创建和操作 C++ 的 Matrix 类实例。以下代码展示如何通过 pybind11 暴露该类。
/*
*
* 简要说明:
* 该文件通过 pybind11 暴露了一个名为 "my_matrix" 的 Python 扩展模块。
* 模块中注册了一个 Matrix 类(C++ 实现),用于在 Python 中创建和操作矩阵对象。
*
* 导出的主要功能(Python 侧):
* - 类名: my_matrix.Matrix
* - 构造器:
* Matrix(rows: int, cols: int)
* 创建一个指定行列数的矩阵(初始内容由底层实现决定)。
* - 实例方法(代表性说明):
* set(i: int, j: int, value)
* 在位置 (i, j) 设置元素值(下标约定以实现为准,通常为 0 基或 1 基,参见实现文档)。
* get(i: int, j: int) -> value
* 返回位置 (i, j) 的元素值。
* rows_num() -> int
* 返回矩阵的行数。
* cols_num() -> int
* 返回矩阵的列数。
* fill_random()
* 用随机值填充矩阵(随机数分布与范围由实现决定)。
* dot(other)
* 矩阵乘法(点乘/矩阵积)。若维度不匹配,应抛出异常或以实现约定处理。
* print()
* 将矩阵内容以可读格式输出(用于调试/展示)。
*
*/
#include <pybind11/detail/common.h>
#include <pybind11/pybind11.h>
#include "matrix.h"
namespace py = pybind11;
PYBIND11_MODULE(my_matrix, m){
py::class_<Matrix>(m, "Matrix")
.def(py::init<int, int>())
.def("set", &Matrix::set)
.def("get", &Matrix::get)
.def("rows_num", &Matrix::rows_num)
.def("cols_num", &Matrix::cols_num)
.def("fill_random", &Matrix::fill_random)
.def("dot", &Matrix::dot)
.def("print", &Matrix::print)
;
}
编写 CMakeLists.txt
要成功构建 Python 扩展模块,需要使用 CMake 对项目进行配置。CMakeLists.txt 文件主要负责指定编译选项、寻找依赖库(如 Python、pybind11),并将 C++ 源文件编译为可供 Python 导入的模块。本节给出完整的 CMake 构建脚本,确保项目可以顺利编译运行。
# 最小 CMake 版本要求
cmake_minimum_required(VERSION 3.14)
# 定义项目名称为 'matrix',并指定项目使用 C++ 语言。
project(matrix LANGUAGES CXX)
# 查找 Python 3 环境。
# COMPONENTS Interpreter Development: 确保找到 Python 解释器和开发头文件/库。
find_package(Python3 REQUIRED COMPONENTS Interpreter Development)
# 查找 pybind11 库。
# REQUIRED: 如果找不到 pybind11,则停止配置并报错。
find_package(pybind11 REQUIRED)
# 设置 C++ 语言标准为 C++11。pybind11 通常至少需要 C++11。
set(CMAKE_CXX_STANDARD 11)
# 强制要求编译器必须支持设置的 C++ 标准
set(CMAKE_CXX_STANDARD_REQUIRED True)
# 设置默认构建类型为 Release。这会启用优化选项。
set(CMAKE_BUILD_TYPE Release)
# 为 Release 构建类型设置高级优化标志 (-O3)
set(CMAKE_CXX_FLAGS_RELEASE "-O3")
# 使用 pybind11 提供的便捷函数来创建 Python 扩展模块。
# 目标名: my_matrix (对应于 Python 中 import my_matrix)
# 源文件: matrix.cpp matrix_bind.cpp
# pybind11 会自动处理链接 Python 库和添加必要的包含目录。
pybind11_add_module(my_matrix matrix.cpp matrix_bind.cpp)
编写 python 脚本
在 Python 脚本中,我们同样定义了一个 Matrix 类,其接口设计与 C++ 版本基本一致,用于保持对比的一致性。在主程序中,我们依次使用下列三种方式执行矩阵乘法:
- 使用 pybind11 导出的 C++ 版本 Matrix 类
- 使用 Python 纯接口实现的 Matrix 类
- 使用 NumPy 的矩阵乘法(高度优化)
通过测量三者的运行时间,便可以直观地比较不同语言、不同实现方式的执行效率。
import my_matrix
import numpy as np
import time
import random
class Matrix:
def __init__(self, rows, cols, data):
self.rows = rows
self.cols = cols
if data is None:
self.data = [0.0] * (rows * cols)
else:
self.data = list(data)
def index(self, row, col):
return row * self.cols + col
def set(self, row, col, value):
if ((row >=0 and row < self.rows) and (col >= 0 and col < self.cols)):
self.data[self.index(row, col)] = value
def get(self, row, col):
if ((row >=0 and row < self.rows) and (col >= 0 and col < self.cols)):
return self.data[self.index(row, col)]
def fill_random(self):
for i in range(self.rows * self.cols):
self.data[i] = random.random()
def dot(self, other):
if self.cols != other.rows:
raise ValueError("Matrix shapes do not match for multiplication")
result = Matrix(self.rows, other.cols, None)
for i in range(self.rows):
for j in range(other.cols):
sum = 0.0
for k in range(self.cols):
sum += self.get(i, k) * other.get(k, j)
result.set(i, j, sum)
return result
if __name__ == "__main__":
a_rows = 100
a_cols = b_rows = 100
b_cols = 400
a = my_matrix.Matrix(a_rows, a_cols)
b = my_matrix.Matrix(b_rows, b_cols)
a.fill_random()
b.fill_random()
start = time.perf_counter()
c = a.dot(b)
elapsed = time.perf_counter() - start
print(f"my matrix compute time: c computed in {elapsed:.6f} s")
a = np.random.rand(a_rows, a_cols).astype(np.float32)
b = np.random.rand(b_rows, b_cols).astype(np.float32)
start = time.perf_counter()
c = np.dot(a, b)
elapsed = time.perf_counter() - start
print(f"numpy compute time: c computed in {elapsed:.6f} s")
a = Matrix(a_rows, a_cols, None)
b = Matrix(b_rows, b_cols, None)
a.fill_random()
b.fill_random()
start = time.perf_counter()
c = a.dot(b)
elapsed = time.perf_counter() - start
print(f"python matrix compute time: c computed in {elapsed:.6f} s")
实验结果
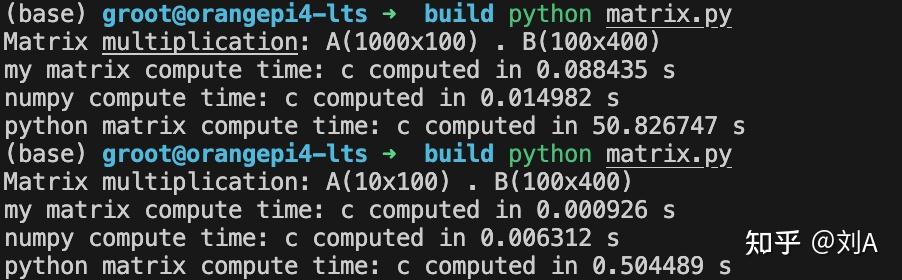
在小规模矩阵乘法中,C++ 实现表现最为出色,NumPy 次之,而纯 Python 的性能最弱。随着矩阵规模增大,NumPy 的优势逐渐显现,在大规模矩阵乘法中性能最优;C++ 紧随其后;纯 Python 与二者相比则存在巨大差距。
文件结构如下:
.
├── build
│ ├── CMakeCache.txt
│ ├── CMakeFiles
│ ├── cmake_install.cmake
│ ├── Makefile
│ ├── matrix.py
│ └── my_matrix.cpython-313-aarch64-linux-gnu.so
├── CMakeLists.txt
├── extern
│ └── pybind11
├── matrix_bind.cpp
├── matrix.cpp
├── matrix.h
├── matrix.py
└── __pycache__


 浙公网安备 33010602011771号
浙公网安备 33010602011771号