LeetCode 排列组合问题回溯

46. 无重复元素的全排列
47. 有重复元素的全排列
784. 字母大小写全排列
93. 复原 IP 地址
301. 删除无效的括号

46. 无重复元素的全排列

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。不限定排列的顺序。Link

不同位置元素交换并回溯结果
以数组 123 为例
- 三个数分别与第 1 个位置进行交换 1；2；3；
  - 后两个数分别与第 2 个位置进行交换 12 13；21 23；32 31；
    - 最后一个数与第 3 个位置进行交换 123 132；213 231；321 312；
    - [1] -> [12,13] -> [123, 132]
    - [2] -> [21, 23] -> [213, 231]
    - [3] -> [32, 31] -> [321, 312]
  - 交换完以后再恢复原状，即回溯

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> ret;
        backtracking(nums, 0, ret);
        return ret;
    }
    void backtracking(vector<int>& nums, int level, vector<vector<int>>& ret) {
        if (level == nums.size()) {
            ret.push_back(nums);
        }
        for (int i = level; i < nums.size(); i++) {
            swap(nums[i], nums[level]); // 与第 level 个位置交换
            backtracking(nums, level + 1, ret); // 递归交换下一个位置
            swap(nums[i], nums[level]); // 回溯交换的结果
        }
    }
};

47. 有重复元素的全排列

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。Link

不同位置元素交换并回溯结果
对于已经交换过的重复元素进行剪枝处理
以数组 1122 为例
所有元素与第一个元素交换，共四种情况 [1, 1, 2, 2]；产生重复
- 建立哈希表存储已经与第一个元素交换过的元素，交换之前检查该元素是否交换过，交换过则直接 continue；否则将该元素加入哈希表并交换。
- 后面每个位置的元素交换同上处理，将已经交换过的元素进行存储。

class Solution {
public:
    vector<vector<int>> ret;
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        backTracking(nums, 0);
        return ret;
    }
    void backTracking(vector<int>& nums, int level) {
        int n = nums.size();
        if (level == n) {
            ret.push_back(nums);
            return;
        }
        set<int> st; // 建立哈希表存储已经交换过的元素值
        for (int i = level; i < n; i++) {
            if (st.find(nums[i]) != st.end()) continue; // 当前元素已经与第 level 个元素交换过，再交换会重复
            st.insert(nums[i]); // 将交换过的元素值放入哈希表中
            swap(nums[i], nums[level]);
            backTracking(nums, level + 1); // 交换下一个位置的元素
            swap(nums[i], nums[level]);
        }
    }
};

依次选择元素进行排列
组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。
与交换不同，排列每次都需要从 0 开始遍历所有元素
从树层上去重
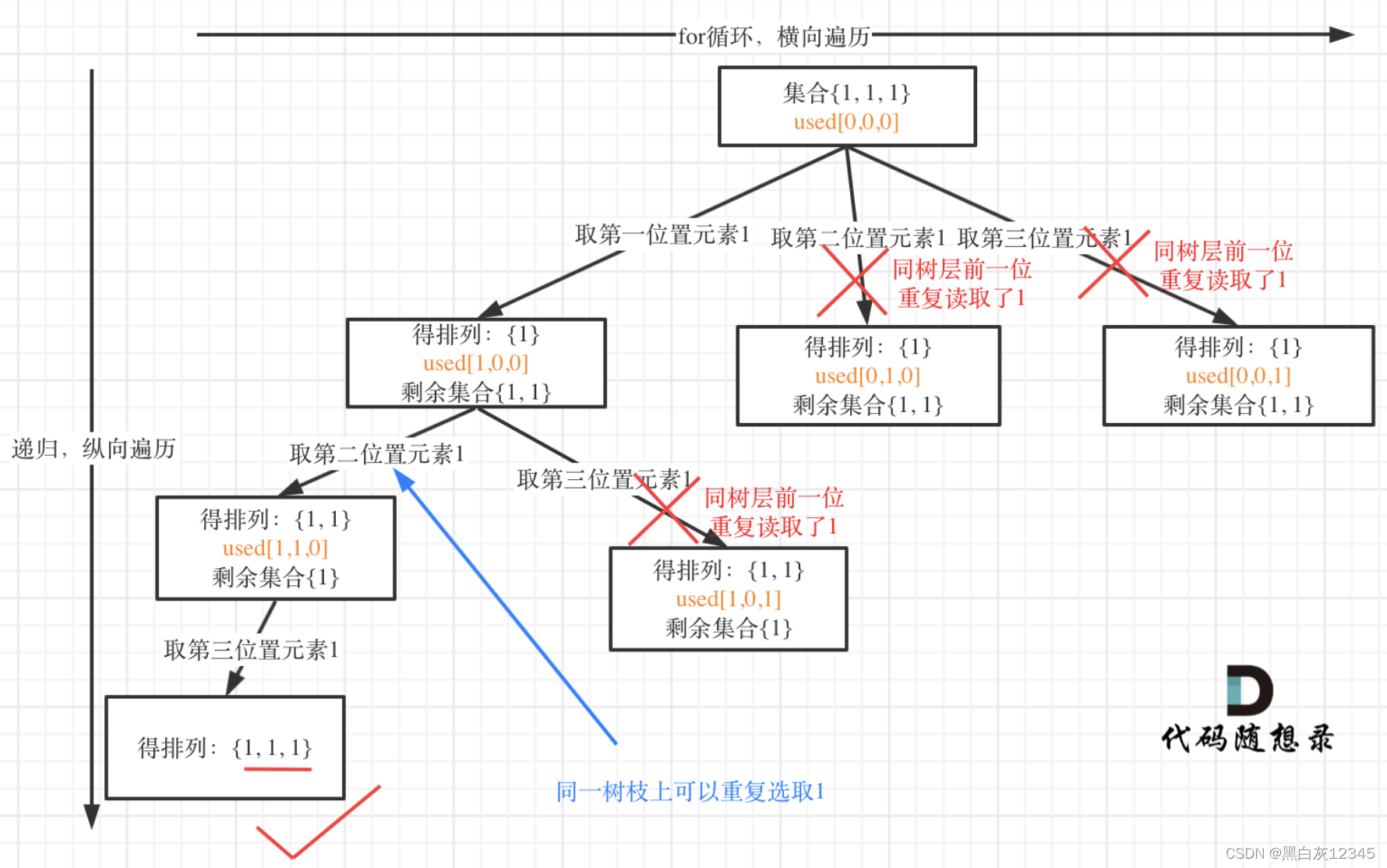
- i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false
从树枝上去重
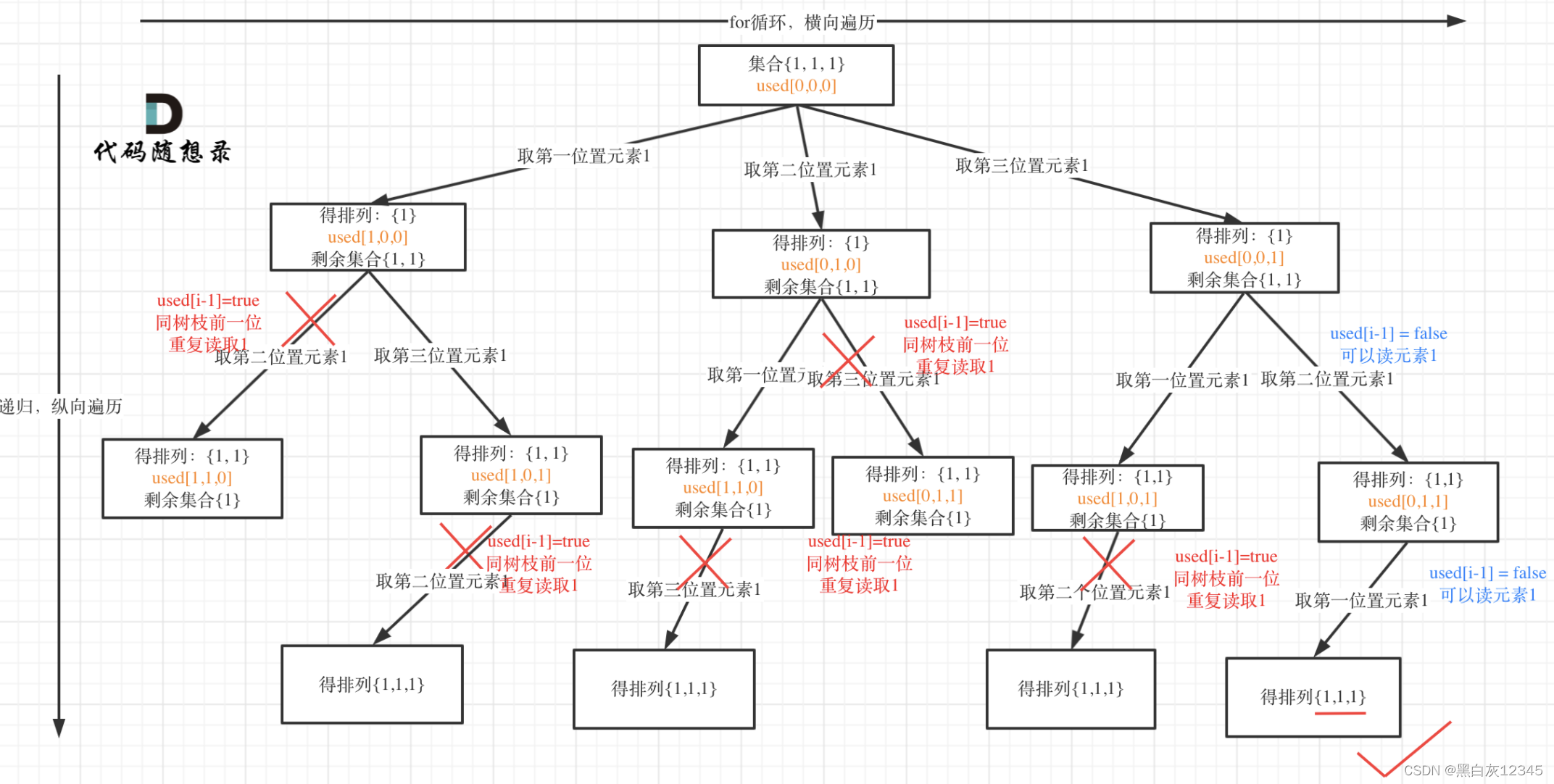
- i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> ans;
    vector<bool> used;
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        this->used = vector<bool>(nums.size(), false);
        sort(nums.begin(), nums.end()); // 排序使相同元素相邻
        backTrack(nums, 0);
        return ret;
    }
    void backTrack(vector<int>& nums, int pos) {
        if (pos == nums.size()) {
            ret.push_back(ans);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            if (used[i]) continue; // 已经用过了当前元素
            // 本层已经用过了当前元素，并且完成了回溯
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
                continue;
            }
            ans.push_back(nums[i]);
            used[i] = true;
            backTrack(nums, pos + 1);
            ans.pop_back();
            used[i] = false;
        }
    }
};

784. 字母大小写全排列

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。返回所有可能得到的字符串集合。以任意顺序返回输出。

与上两个数字的全排列思路相同，但此处不需要交换元素，仅需要改变大小写
从第一个字符开始递归
- 保持字符不变递归
- 改变字符大小写递归，递归结束回溯

class Solution {
public:
    int number;
    vector<string> ret;
    vector<string> letterCasePermutation(string s) {
        this->number = 'a' - 'A';
        backtracking(s, 0);
        return ret;
    }
    void backtracking(string& s, int i) {
        int n = s.size();
        if (i == n) {
            ret.push_back(s);
            return;
        }
        backtracking(s, i + 1); // 当前字符不变号向下递归
        // 改变当前字母的大小写向下递归，回溯结果
        if (s[i] >= 'a' && s[i] <= 'z') {
            s[i] -= number;
            backtracking(s, i + 1);
            s[i] += number;
        }else if (s[i] >= 'A' && s[i] <= 'Z') {
            s[i] += number;
            backtracking(s, i + 1);
            s[i] -= number;
        }
    }
};

上述方法再遇到非字母时也会向下递归，递归就意味着当前结果入栈，当字符串长度过长时，可能会栈溢出，可以采用 for 循环进行剪枝，减少不必要的递归

当前符号非字母
- 直接跳过判断下一符号
当前符号为字母
- 不改变大小写向下递归
- 改变大小写向下递归并回溯
- break 退出 for 循环，剩余字母会在递归中进行处理
最后一个字符非字母时，可能无法递归保存结果，因为需要直接对最后一个字符进行判断

isalpha() 函数可以用来判断当前字符是否为字母
isdigit() 函数可以用来判断当前字符是否为数字
s[i] ^= ' '；字母与空格异或的结果相当于改变了它的大小写

class Solution {
public:
    vector<string> res;
    vector<string> letterCasePermutation(string s) {
        backtracking(s, 0);
        return res;
    }
    void backtracking(string& s, int index) {
        int n = s.size();
        if (index == n) {
            res.push_back(s);
            return;
        }
        for (int i = index; i < n; i++) {
            if (isalpha(s[i])) {
                backtracking(s, i + 1);
                s[i] ^= ' ';
                backtracking(s, i + 1);
                s[i] ^= ' ';
                break; // 当前字母递归结束，直接 break
            }
            if (i == n - 1) {
                res.push_back(s); // 对最后一个字符非字母进行处理
            }
        }
    }
};

93. 复原 IP 地址

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。Link

四个分割点的排列组合
剪枝的条件
- 段长度不为 1，但是却以 0 开头的情况：01、023
- 段长度为 3，但是数值不合法的情况：256、432
- 剩余字符过多的情况：192.168.128.128，如 1.92xxx、19.2xxx均不合法

class Solution {
public:
    vector<string> res;
    string temp;
    vector<string> restoreIpAddresses(string s) {
        dfs(s, 0, 0);
        return res;
    }
    // idx - 本次遍历字符串的起始位置
    // seg - 本次属于第几段 ip 地址
    void dfs(string& s, int idx, int seg) {
    	// 字符使用完毕，并且划分了 4 段
        if (idx == s.size() && seg == 4) {
            temp.pop_back();
            res.push_back(temp);
            return;
        }

        string str;
        for (int i = 0; i < 3; i++) {
            str += s[idx + i];
            // 诸如 023、256 这种不合法数值
            if (i != 0 && str[0] == '0') break;
            if (i == 2 && str > "255") break;
            // 当前索引为 idx + i，剩下的字符数为 size - idx - i - 1
            // 确保剩下的字符数量能够被余下的 3 - seg 段完全划分
            if ((s.size() - idx - i - 1) > (3 - seg) * 3) continue;
            // 保存当前结果、以便进行回溯
            string prev = temp;
            temp += str + '.';
            dfs(s, idx + i + 1, seg + 1);
            temp = prev;
        }
    }
};

301. 删除无效的括号

给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。

返回所有可能的结果。答案可以按任意顺序返回。Link

暴力搜索、剪枝、去重
1、确定删除的最小数量
- 遇到 '(' : L++
- 遇到 ')' : 1、左括号数量不为0：L--；2、左括号数量为0: R++；
- L、R表示了无法进行匹配的左、右括号数量，也是删除的最小数量，可得有效字符串的长度为 n - L - R
2、确定最多的括号对数
- 遇到 '(' : L1++
- 遇到 ')' : R1++
- 最多的括号对数便是 min(L1, R1)
- 遇到左括号可以考虑为 score + 1，遇到右括号则 score - 1，这样 score 可以反映字符串是否合法
4、剪枝条件
- 删除了过多的符号：L < 0 || R < 0
- 当前字符串不合法：score < 0 || score > min(L1, R1)，即右括号过多｜｜左括号过多
- 字符串的字符访问完毕
5、引入 set 去重

class Solution {
public:
    set<string> st;
    int n, len, Max;
    vector<string> removeInvalidParentheses(string s) {
        this->n = s.size();
        // 1、确定需要删除的左、右括号个数
        int l = 0, r = 0;
        for (char &c : s) {
            if (c == '(') {
                l++;
            }else if (c == ')') {
                if (l != 0) l--;
                else r++;
            }
        }
        this->len = n - l - r;

        // 2、确定左、右括号的个数
        int c1 = 0, c2 = 0;
        for (char &c : s) {
            if (c == '(') {
                c1++;
            }else if (c == ')') {
                c2++;
            }
        }
        this->Max = min(c1, c2);

        // 递归
        dfs(0, "", s, l, r, 0);
        vector<string> ret;
        if (st.empty()) return ret;
        for (auto& s : st) {
            ret.push_back(s);
        }
        return ret;
    }

    void dfs(int idx, string cur, string& s, int l, int r, int score) {
        // 左、右括号删多了；当前位置右括号大于了左括号个数、左括号大于了右括号个数
        if (l < 0 || r < 0 || score < 0 || score > Max) {
            return;
        }
        // 删完了，符合最大长度
        if (l == 0 && r == 0) {
            if (cur.size() == len) {
                st.insert(cur);
                return;
            }
        }
        // 字符遍历完了
        if (idx == n) return;
        
        char ch = s[idx];
        if (ch == '(') {
            dfs(idx + 1, cur + ch, s, l, r, score + 1); // 加入当前左括号
            dfs(idx + 1, cur, s, l - 1, r, score); // 删除当前括号
        }else if (ch == ')') {
            dfs(idx + 1, cur + ch, s, l, r, score - 1); // 加入当前右括号
            dfs(idx + 1, cur, s, l, r - 1, score); // 删除当前括号
        }else {
            dfs(idx + 1, cur + ch, s, l, r, score); // 加入无关字符
        }
    }
};

posted @ 2023-02-15 21:16 GreyWang 阅读(59) 评论(0) 收藏举报

刷新页面返回顶部

GreyWang

LeetCode 排列组合问题 回溯

46. 无重复元素的全排列

47. 有重复元素的全排列

784. 字母大小写全排列

93. 复原 IP 地址

301. 删除无效的括号

公告

LeetCode 排列组合问题回溯