斜率优化 DP 学习笔记
简介
前置知识:凸包的概念以及如何求二维凸包。
考虑线性动态规划的一类转移,可以整理为以下形式:
其中,\(f_1(i)\) 为仅关于 \(i\) 的某些信息的多项式,\(f_2(j)\) 为仅关于 \(j\) 的某些信息的多项式;\(g(i) \cdot h(j)\) 是两个这样的多项式的乘积。
根据情况的不同,这一类转移可以通过斜率优化的思想进一步优化到 \(\mathcal O(n) \sim \mathcal O(n \log^2 n)\) 的复杂度。
例题:P3195 [HNOI2008] 玩具装箱
一句话题意:给定一个长度为 \(n\) 的数列 $c_i $和一个常数 \(L\),要求把该数列划分成若干段,每段 \([l,r]\) 的代价为 \((r-l + \sum_{i=l}^{r} c_i - L)^2\)。求各段划分代价之和的最小值。
预处理 \(c_i\) 的前缀和 \(s_i\),根据题意可以列出转移方程:
令 \(S_i = s_i+i\),\(L \gets L+1\),则方程可以化为:
思考方式 1(数形结合)
不妨设 \(i\) 的最优决策点为 \(j\),去掉等号右边的 \(\min\),移项得
令
原式化为
这不是我们熟悉的一次函数表达式吗?对于一个固定的 \(i\),其斜率 \(k\) 是固定的,y 轴上的截距 \(b\) 和 \(dp_i\) 的大小有关。
还记得我们的目标是最小化 \(dp_i\) 吗?既然要最小化 \(dp_i\),那必然要最小化截距。
于是问题就变为了,选择一个点 \((x_j,y_j)\),作一条经过该点斜率已知为 \(k\) 的直线,使得它 y 轴上的截距最小。
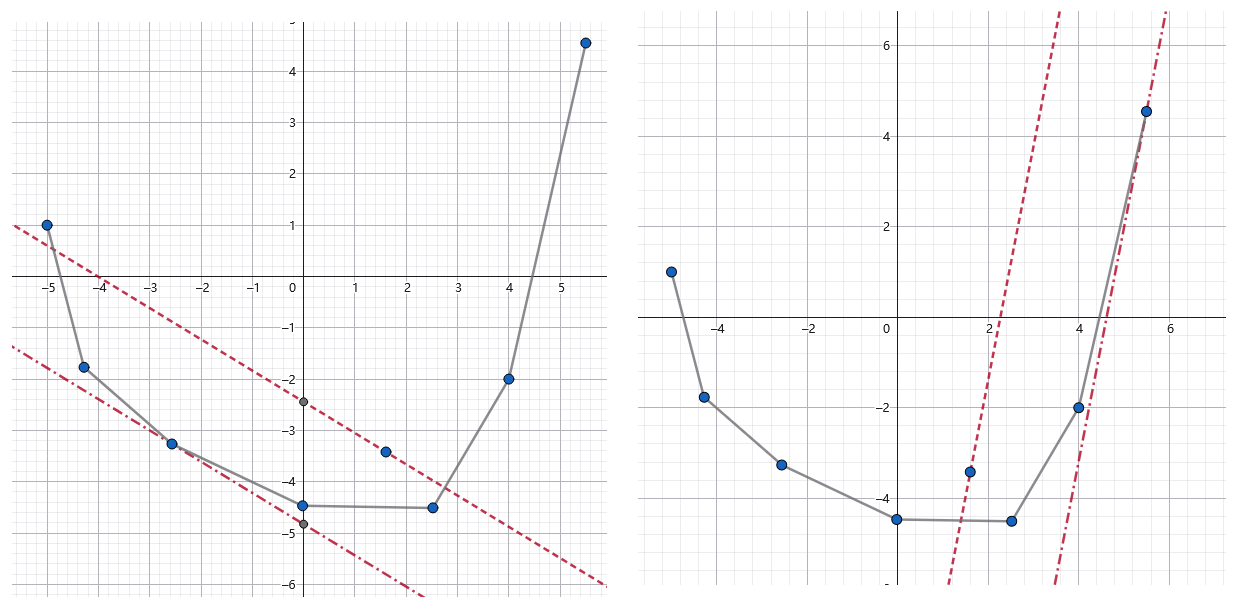
如果你熟悉线性规划的话,会意识到这是一个线性规划问题(虽然这并不是很重要)。不难发现最优决策点在下凸包上取到。
如下图,可以自己手画帮助理解:
本题中,注意到每次加入的点 \((S_i,S_i^2+dp_i)\) 横坐标 \(S_i\) 是单调递增的,可以单调栈实时插入一个点维护凸包。
又注意到 \(k=2(S_i-L)\) 这个斜率是单调递增的,那么最优决策点满足决策单调性。具体来说,参考上面两张图,斜率越大,取得最小截距的点就越靠后。
由于转移的位置只增大不减小,我们不妨一边找下一个决策点一边把前面的凸壳扔掉,也就是把单调队列改成单调栈来做这件事。时间复杂度 \(\mathcal O(n)\)。
方法 1 代码实现,256062208
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
typedef long long ll;
typedef pair<ll, ll> Point;
#define x first
#define y second
#define sq(x) ((x) * (x))
int n, hh, tt, q[N];
ll L, S[N], dp[N];
inline double slope(int i, int j) { // 计算斜率
Point a(S[i], S[i] * S[i] + dp[i]), b(S[j], S[j] * S[j] + dp[j]);
if (a.x == b.x) return 1e14; // 注意横坐标差为 0 时斜率为无穷大,虽然本题用不到
return 1.0 * (a.y - b.y) / (a.x - b.x);
}
inline ll calc(int j, int i) { return sq(S[i] - S[j] - L) + dp[j]; } // 计算 j 向 i 转移的答案
int main() {
scanf("%d%lld", &n, &L); L++;
for (int i = 1; i <= n; ++i) scanf("%lld", &S[i]), S[i] += S[i - 1] + 1;
q[hh = tt = 1] = 0;
for (int i = 1; i <= n; ++i) {
while (hh < tt && calc(q[hh], i) >= calc(q[hh + 1], i)) hh++; // 如果凸包的下一个点比目前决策点优,用不着,将其弹掉
dp[i] = calc(q[hh], i);
while (hh < tt && slope(q[tt - 1], q[tt]) >= slope(q[tt], i)) tt--; // 维护下凸包
q[++tt] = i;
}
printf("%lld\n", dp[n]);
return 0;
}
思考方式 2(推式子,分析单调性)
感谢:@Microscopic_WaXeR,用这种方法第一次让我学会斜率优化。
不妨设有前后两个决策点 \(j_1<j_2\),钦定前面的不比后面更优。
那么有
展开并整理得
同样,令 \(k_i=2(S_i-L)\),\(x_j=S_j\),\(y_j=S_j^2+dp_j\)。
那么:后一个点不劣于前一个点,当且仅当两点之间直线斜率 \(\le 2(S_i-L)\)。
对于当前所有可能的决策点,我们把它存入一个队列,其中队头是当前的最优决策点。下面要证明这个序列是关于两点之间斜率单调递增的。
假如我们有三个点 \(x_a<x_b<x_c, k_{ab}\le k_{bc}\)。
假设有 \(k_{ab} \le 2(S_i-L)\),那么肯定有 \(k_{bc} \le 2(S_i-L)\),这时一定选 \(c\),因为选 \(a\) 不如选 \(b\)、选 \(b\) 不如选 \(c\);
假设有 \(k_{bc} \le 2(S_i-L)\) 但 \(k_{ab} > 2(S_i-L)\),那我肯定也选不到 \(b\),因为选 \(a\) 或选 \(c\) 都比选 \(b\) 优;
假设这两个斜率都大于 \(2(S_i-L)\),同理一定选 \(a\)。
综上,当斜率局部递减时,可以直接删去中间的而不影响答案。
于是直接维护关于斜率的单调队列;每次查询答案时,不断弹出队头直到队首的两个点斜率 \(>2(S_i-L)\) 为止,取队首的点转移即可。由于 \(2(S_i-L)\) 单调递增有了正确性保证。
复杂度同样也是 \(\mathcal O(n)\)。和上面的做法本质是同一个东西。
思考方式 3(平面向量)
来自:杜老师(xudyh)。
前置知识:高中数学必修二,向量的内积(数量积)。
重新看拆完以后的转移式子 \(dp_i = \min_{j<i}\{(S_j^2+dp_j)-2(S_i-L) \cdot S_j\}+(S_i-L)^2\)。
观察 \(\min\) 里面的东西,考虑它的实质是什么。发现可以把它化为向量内积的形式 \((-2(S_i-L),1) \cdot (S_j,S_j^2+dp_j)\)!
向量内积的值又可以表示为 \(|a||b|\cos \theta\),即一个向量在另一个向量上的投影与另一个向量大小的乘积。那么只要选择一个向量 \((S_j, S_j^2+dp_j)\) 使得它在 \((-2(S_i-L),1)\) 方向上的投影最大就可以了!
注意到 \((-2(S_i-L),1)\) 的角度的正切值(即向量所在直线的斜率)\(-\frac{1}{2(S_i-L)}\) 单调递增,所以最优决策点也是单调递增的。
套用方法 1 的算法即可。这一方法的好处在于避免了进一步分析。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号