决策单调性 / 四边形不等式优化 DP 做题笔记
最优决策点分治
CF321E Ciel and Gondolas
\(w(x,y)\) 满足四边形不等式,证明:
P4767 [IOI 2000] 邮局 加强版
注意到 \(w(l,r)\) 有递推 \(w(l,r)=w(l,r-1)+x_r-x_{\lfloor(l+r)/2\rfloor}\):
-
\([l,r-1]\) 区间长度为奇数,添加 \(r\) 后中位数还是 \(\lfloor\frac{l+r}{2}\rfloor\)
-
\([l,r-1]\) 区间长度为偶数,添加 \(r\) 后中位数位置 \(+1\),但由于原 \(\text{mid}\) 在中间两个数之间任意取,所以位置 \(+1\) 不影响前面的答案
\(w\) 满足四边形不等式,证明:
\(w(l,r+1)=w(l,r)+x_{r+1}-x_{\lfloor(l+r+1)/2\rfloor} \cdots \textcircled{1}\)
\(w(l-1,r+1)=w(l-1,r)+x_r-x_{\lfloor(l+r)/2\rfloor} \cdots \textcircled{2}\)
\(\textcircled{1} - \textcircled{2}, w(l,r+1)+w(l-1,r)=w(l,r)+w(l-1,r+1)+\underline{x_{\lfloor(l+r)/2\rfloor}-x_{\lfloor (l+r+1)/2\rfloor}, \le 0}\)
\(w(l,r+1)+w(l-1,r) \le w(l,r)+w(l-1,r+1)\),推广即得结论
void solve(int l,int r,int ql,int qr){
if(l>r) return;
int mid=(l+r)/2,qmid;
for(int i=ql;i<=min(qr,mid-1);++i)
if(g[i]+w[i][mid]<f[mid])
qmid=i, f[mid]=g[i]+w[i][mid];
solve(l,mid-1,ql,qmid);
solve(mid+1,r,qmid,qr);
}
CF834D The Bakery
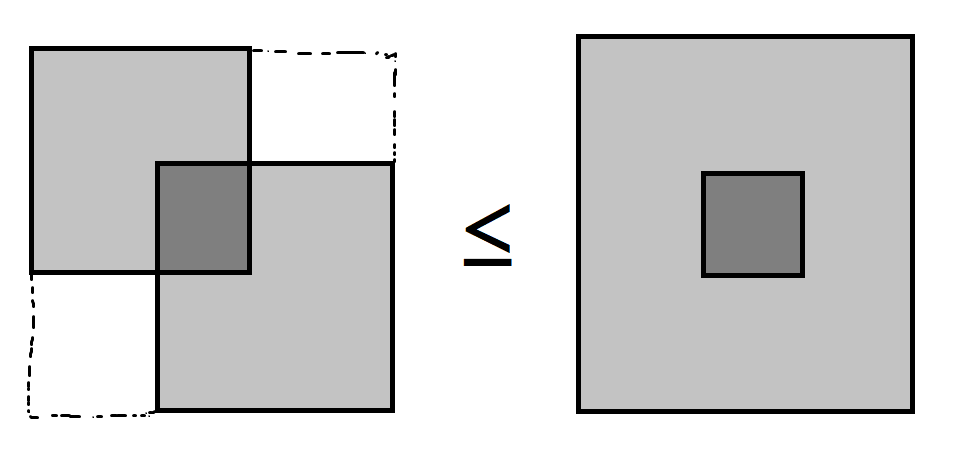
其中 \(w(l,r)\) 表示 \([l,r]\) 不同颜色的种数。
\(w\) 满足四边形不等式,证明:
即证明\[|A \cup B|+|B \cup C| \ge |A \cup B \cup C|+|B| \]\[|A|+2|B|+|C|-|A \cap B|-|B \cap C| \ge |A|+2|B|+|C|-|A \cap B|-|B \cap C|-|A \cap C|+|A \cap B \cap C| \]\[|A \cap C - B| \ge 0 \]显然成立。
现在问题就变为如何快速求 \(w(l,r)\)。若使用主席树维护,加个分治复杂度为 \(O(kn \log^2 n)\),容易被卡。
考虑这个怎么做到一只 \(\log\)。使用一个类似莫队的 trick,分治过程中暴力调整左右端点计算答案。由于分治时查询的区间具有一定连续性,移动左右端点的复杂度大概是和分治同阶的。然后总复杂度就是 \(O(kn \log n)\)。
CF868F Yet Another Minimization Problem
和上面那个差不多的题,只不过前者贡献为 \(\sum [\text{cnt}(i)>0]\) 这个是 \(\sum \binom{\text{cnt}(i)}{2}\)。
做法大致相同。需要开 long long。
P3515 [POI 2011] Lightning Conductor
与 DP 不相干的决策单调性例题。
注意到这个绝对值很难看,套路地,分 \(j<i\) 与 \(j>i\) 两种情况去掉绝对值。
不妨令 \(j<i\),令 \(g_j=h_j,w(j,i)=\sqrt{i-j}\),可以看出来标准形式 \(f_i=\max\{g_j+w(j,i)\}\)。
下面证明 \(w(x,y)=\sqrt{y-x}\) 满足四边形不等式。
\(a<b<c<d\),证明:\(\sqrt{c-a}+\sqrt{d-b} \ge \sqrt{d-a}+\sqrt{c-b}\)
令 \(x=b-a, y=c-b, z=d-c\),即证明:\(\sqrt{x+y}+\sqrt{y+z} \ge \sqrt{x+y+z}+\sqrt{y}\)
\[x+2y+z+2\sqrt{(x+y)(y+z)} \ge x+2y+z+2\sqrt{(x+y+z)y} \]\[xy+xz+y^2+yz \ge xy+y^2+yz \]\[xz \ge 0 \]显然成立。
重要细节:\(\lceil\sqrt{y-x}\rceil\)(上取整)是不满足四边形不等式的,所以最优决策点要用原始根号计算,最后答案再上取整。
ABC348G Max (Sum - Max)
把所有二元组 \((A_i,B_i)\) 按照 \(B_i\) 从小到大排序。若钦定子集 \(B\) 的最大值在 \(i\) 处取得,那么也就是要在下标 \(<i\) 的位置中选 \(k-1\) 个最大的 \(A_j\)。静态查询前缀最大 \(k\) 个数的和,可以主席树上二分以单次 \(O(\log n)\) 的复杂度解决。
对于 \(k=1\dots n\),设 \(S_k\) 表示任意一个取 \(k\) 个元素时 \(f(S)=\sum A_i - \max B_i\) 取得最大值的子集,\(p(k)\) 为这种子集最小的最大下标。下面证明 \(p(k)\) 具有决策单调性,即 \(\forall x<y, p(x) \le p(y)\)。
根据之前的讨论有 \(\displaystyle f(S_k) = \sum_{i\in S_k, i\neq p(k)} A_i + A_{p(k)} - B_{p(k)}\)。
现要证明 \(\forall j<p(k_0)\),在取 \(k>k_0\) 个元素时 \(j\) 不优于 \(p(k_0)\)。这个显然,因为当 \(k\) 增大时,\(j\) 在 \(p(k_0)\) 前,就导致 \(\sum A_i\) 中 \(p(k_0)\) 能选的比 \(j\) 多,本来优现在只可能更优。
然后就可以分治做。注意离散化。
二分队列
P1912 [NOI2009] 诗人小G
发现前面和后面的答案具有关联,不能直接分治做。若套一个 CDQ 仍能分治,代价为时间复杂度多一只 log。
下面介绍决策单调性的二分队列算法。
考虑用一个队列实时维护 \(>i\) 的点在 \(0 \sim i\) 的最优决策点。每算出一个 \(i\) 的答案就往后更新,看能否成为后面点的最优决策点。根据决策单调性,队列中前面点的最优决策点不大于后面点。某些点的最优决策点相同合并成一段处理。
根据决策单调性 \(i\) 必然是更新了某一个后缀的最优决策点。对于 \(i\) 比末尾某一段的最优决策点都优的,就直接替换整段;否则在末尾一段中二分寻找分界点。具体见代码。
回到本题。
令 \(h(x)=|x-L-1|^p\),则 \(w(j,i)=h(s_i-s_j)\)。观察到 \(h(x)\) 是凹函数,\(s_i-s_j>0\)。下面证明满足四边形不等式:
\(a<b<c<d, h(s_c-s_a)+h(s_d-s_b) \le h(s_d-s_a)+h(s_c-s_b)\)
令 \(x=s_b-s_a, y=s_c-s_b, z=s_d-s_c\)
\(h(x+y)+h(y+z) \le h(x+y+z)+h(y)\)
\(h(x+y)-h(y) \le h(x+y+z)-h(y+z)\)
令 \(\Delta=x, h(y+\Delta)-h(y) \le h(y+z+\Delta)-h(y+z)\)
由凸函数的性质得,对于确定的 \(\Delta\),若 \(p<q\) 则有 \(h(p+\Delta)-h(p)<h(q+\Delta)-h(q)\),符合上面形式,上式得证。
q[hh=tt=1]={1,0};
for(int i=1;i<=n;++i){
if(hh<=tt&&q[hh].first<i) q[hh].first++;
if(hh<tt&&q[hh].first>=q[hh+1].first) hh++;
pre[i]=q[hh].second;
dp[i]=w(pre[i],i);
while(hh<=tt&&w(q[tt].second,q[tt].first)>=w(i,q[tt].first)) tt--;
if(hh<=tt){
int l=q[tt].first,r=n,ans=-1;
while(l<=r){
int mid=(l+r)/2;
if(w(q[tt].second,mid)>=w(i,mid)) ans=mid, r=mid-1;
else l=mid+1;
}
if(ans>0) q[++tt]={ans,i};
}
else q[++tt]={i,i};
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号