KMP 字符串匹配及基础应用
CSP 考前一个多月,发现自己字符串学的都忘完了,顺便开个坑。
第二版修订时间:2025/3/21;持续更新中。
\(\texttt{KMP}\) 算法(板题 洛谷 P3375)
-
名称:KMP (Knuth-Morris-Pratt) 字符串匹配算法
-
作用:在母串 \(S\) 内,查找某子串 \(P\)(称为“模式串”)的所有出现位置。
-
时间复杂度:线性(串长级别)
-
算法流程:
-
预处理并计算 \(\text{next}\) 数组;
-
利用上一步的结果进行字符串匹配。
-
下面将分别讲解这两个部分的实现。约定 \(n=|P|, m=|S|\)。
1. \(\text{next}\) 数组是什么?
对于一个长度为 \(\text{len}\) 的字符串 \(s\),它的 \(\text{border}\) 定义为:
-
满足 \(\large s_{[1,k]}=s_{[\text{len}-k+1,\text{len}]} \normalsize, k<\text{len}\) 的所有前缀 \(\large s_{[1,k]}\)。
-
显然,\(\text{border}\) 是 \(s\) 的一个子串,且它同时是 \(s\) 的真前缀与 \(s\) 的真后缀。
然后对于上文给出的模式串 \(P\),我们定义其中长度为 \(i\) 的前缀的 \(\text{next}\) 值为:
即 \(\large P_{[1,i]}\) 的最长 \(\text{border}\) 的长度。
注:\(\text{next}\) 数组,又名 LPS Table,即 Longest Prefix which is also Suffix。
不难发现关于 \(\text{next}\) 的两个关键性质:
-
\(\text{next}[i]<i\)(定义)。
-
\(\text{next}[i]\) 是 \(\large P_{[1,i]}\) 最长 \(\text{border}\) 的长度;
\(\text{next}[\text{next}[i]]\) 是 \(\large P_{[1,i]}\) 次长 \(\text{border}\) 的长度……
以此类推,嵌套的 \(\text{next}\) 恰好依次对应 \(\large P_{[1,i]}\) 的所有 \(\text{border}\)。
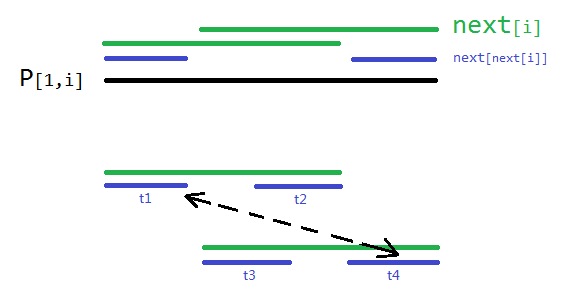
- 对以上一点的说明(如上图):
根据 \(\text{next}\) 的定义有 \(t_1=t_3,t_2=t_4\);
根据 \(\text{next}[\text{next}[i]]\) 的定义,有 \(t_1=t_2\)。
所以有 \(t_1=t_4\),于是 \(\text{next}[\text{next}[i]]\) 对应 \(\large P_{[1,i]}\) 的 \(\text{border}\)。显然这个 \(\text{border}\) 是除了 \(\text{next}[i]\) 最大的,这符合 \(\text{next}[\text{next}[i]]\) 的定义。
其他嵌套情形同理。
2. 如何高效地求 \(\text{next}\)?
由 \(\text{next}[i]<i\),约定 \(\text{next}[1]=0\)。
对于 \(P\) 中的位置 \(i\),假设我们已经求出 \(\text{next}[1] \sim \text{next}[i-1]\),考虑如何求 \(\text{next}[i]\)。
对于 \(\text{next}[i]\):
-
如果 \(P_1 \neq P_i\),那么 \(\large P_{[1,i]}\) 没有 \(\text{border}\),记 \(\text{next}[i]=0\)。
-
否则,它一定接在 \(\large P_{[1,i-1]}\) 的某个 \(\text{border}\) 后面(见下图),于是有:
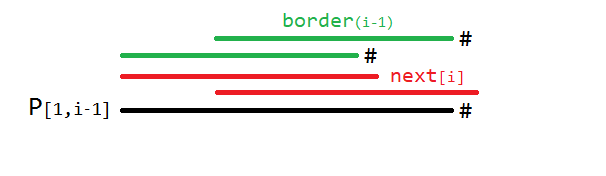
可以得到下面的算法:
令变量 \(j\) 初始为 \(\text{next}[i-1]\)。
比较 \(P_i\) 与 \(P_{j+1}\),分两种情况讨论:
- 如果 \(P_i = P_{j+1}\),说明 \(\large P_{[1,i]}\) 中长度为 \(j\) 的前缀向后扩展一位后,仍然等于其同样长的后缀。这符合 \(\text{next}\) 的定义,因此 \(\text{next}[i] = j+1\)。
- 否则,找到 \(\large P_{[1,i-1]}\) 的下一个 \(\text{border}\);令 \(j \leftarrow \text{next}[j]\),重新比较。
参考代码(C++):
nxt[1] = 0;
for (int i = 2, j = 0; i <= n; ++i) {
while (j && P[i] != P[j + 1]) j = nxt[j];
if (P[i] == P[j + 1]) j++;
nxt[i] = j;
}
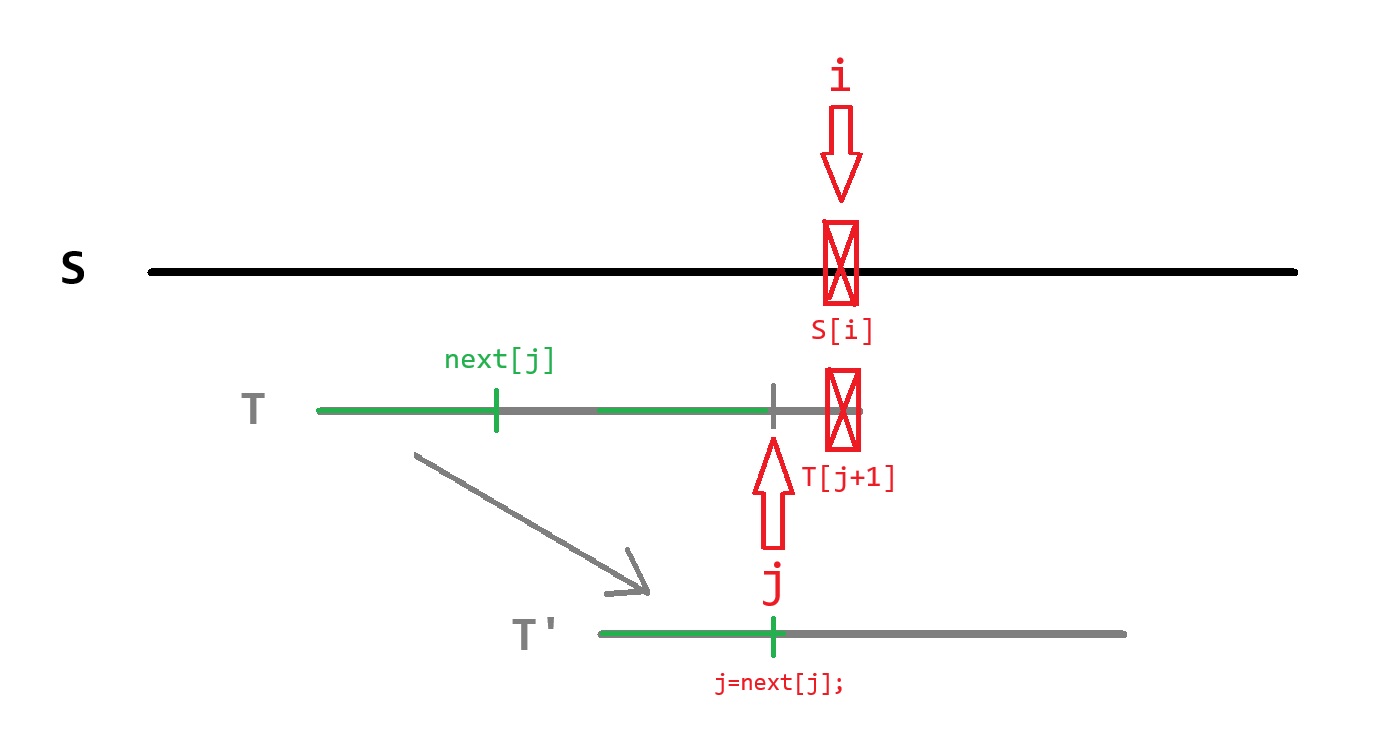
3. 有了 \(\text{next}\) 数组,如何匹配?
假如我们已经求出了 \(\text{next}[1] \sim \text{next}[n]\),考虑利用其进行子串匹配。
对于 \(S\) 中的每一个位置 \(i\),令变量 \(j\) 表示模式串 \(P\) 已经匹配完了 \(j\) 个字符。
其初值表示上次已经匹配到了 \(P_j\) 的位置,即以 \(S_{i-1}\) 结尾的一段长度为 \(j\) 的后缀与 \(\large P_{[1,j]}\) 是匹配的。
现在我们检查 \(P_{j+1}\) 是否与 \(S_i\) 匹配。(步骤 A)
-
如果相等,那么 \(S\) 与 \(P\) 又往后多匹配了一位,转步骤 B。
-
如果不等,参照我们在上一节中的处理方法,令 \(j=\text{next}[j]\),然后回到步骤 A。
接着让 \(i\) 和 \(j\) 分别 \(+1\),继续匹配下一个字符。(步骤 B)
如果在某一时刻有 \(j=n\),那么说明 \(\large S_{[i-n+1,i]} \normalsize = P\),匹配成功。令 \(j=\text{next}[j]\) 继续匹配。

参考代码(C++):
for (int i = 1, j = 0; i <= m; ++i) {
while (j && S[i] != P[j + 1]) j = nxt[j];
if (S[i] == P[j + 1]) j++;
if (j == n) {
printf("Found pattern! Begins at: %d\n", i - n + 1);
j = nxt[j];
}
}
4. 复杂度证明
结论:上述两部分合起来的时间复杂度是 \(\mathcal O(n+m)\)。
先分析求 \(\text{next}\) 的复杂度。不难发现,复杂度主要由两部分组成:
-
if (P[i] == P[j + 1]) j++;
这一行复杂度是 \(\mathcal O(1)\) 的,最多会使指针 \(j\) 向后跳 \(1\) 位。 -
while (j && P[i] != P[j + 1]) j = nxt[j];
由于 \(\text{next}\) 的一条性质 \(\text{next}[i]<i\),指针 \(j\) 一定会不断向前跳。
于是我们所分析的就变成了这样一个问题:
-
数轴上有一个点,初始在 \(0\) 的位置。
-
每秒先向后跳一步(长度为 \(1\) 格),再向前跳若干步,且始终在原点或其右侧。
-
时间复杂度即为该点跳的步数。
显然向后跳的时间复杂度累加起来是 \(\mathcal O(n)\)。考虑在向前跳的过程中,每向前跳一步,必然重复走了之前向后跳的若干步,并且由于 \(j\) 向前跳的过程中不能折返,向后跳的每步,至多对应向前跳的一步。所以向前跳的步数是 \(\le \mathcal O(n)\) 的,总复杂度为 \(\mathcal O(n)\)。
匹配部分同理。
提示:一般情况下,对于朴素的字符串匹配问题,使用字符串哈希可以达到与 KMP 相同的复杂度。
循环节问题(板题 洛谷 P4391)
待补充
哦对了,还有一道最长循环节问题,可以留作思考~
带删的字符串匹配(板题 洛谷 P4824)
待补充
Z 函数 / 扩展 KMP(板题 洛谷 P5410)
待补充
一些待完成的习题
更多请参见 OI-wiki
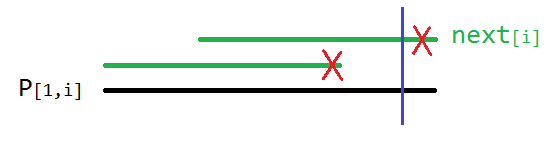
如果 \(\text{next}[i]>0\),那么 \(\large P_{[1,i]}\) 有一个长度为 \(\text{next}[i]\) 的 \(\text{border}\)。根据下图,\(\large P_{[1,i-1]}\) 就必然有一个长度为 \(\text{next}[i]-1\) 的 \(\text{border}\)。即得到不等式:
所以 \(\text{next}[i] \le \text{next}[i-1]+1\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号