GRPO详解

GRPO详解

GRPO算法是在PPO算法的基础上进化而来的，在搞清楚GRPO算法前，需要先了解PPO算法是如何在LLM的Post Training中应用的。

本文主要参考DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models。

论文链接：https://arxiv.org/abs/2402.03300

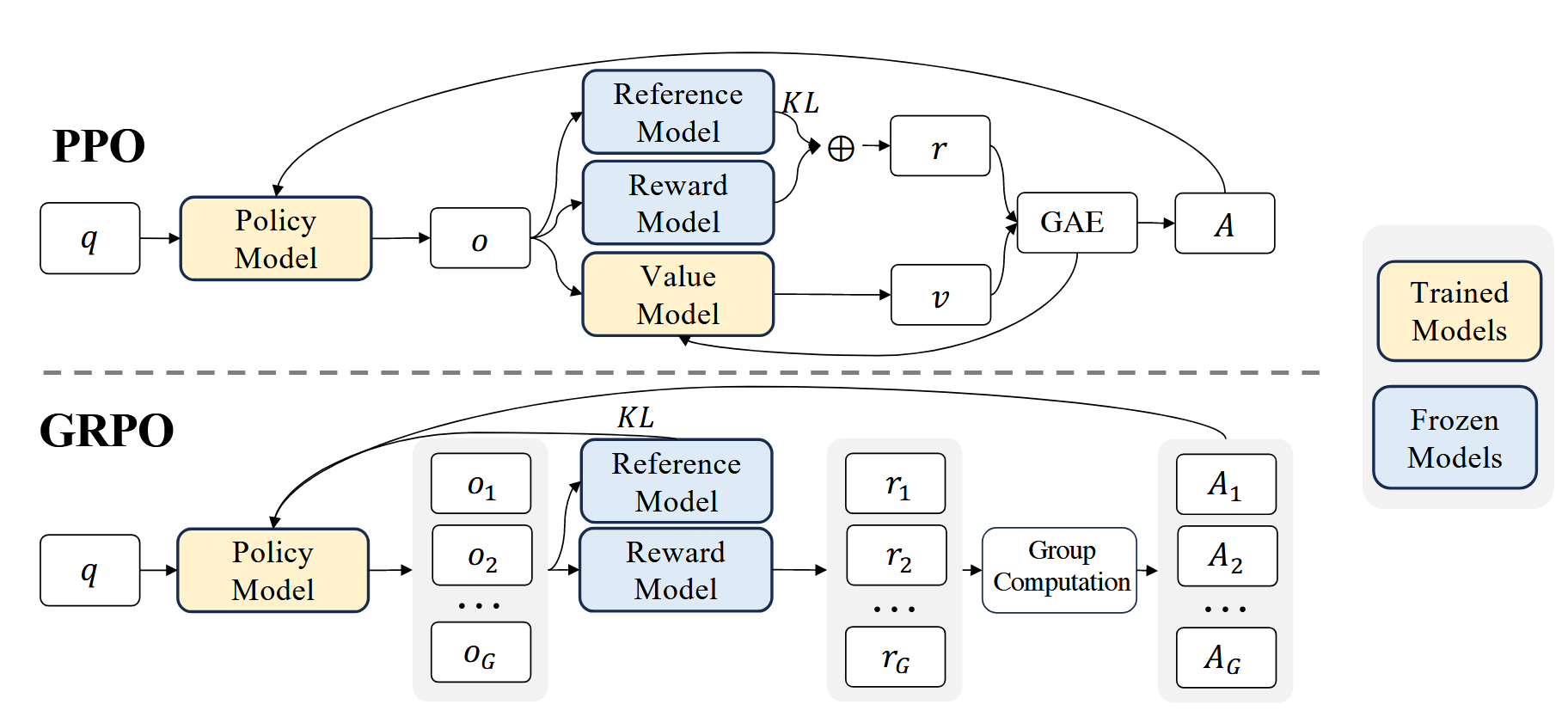
PPO概述

PPO的理论基础已在 https://www.cnblogs.com/GreenOrange/articles/18582769 给出，这里只简述PPO在LLM中的应用。

其中最常用用法如下,目标是最大化\(\mathcal{J}_{PPO}(\theta)\)：

\[\mathcal{J}_{PPO}(\theta) = \mathbb{E}[q \sim P(Q), o \sim \pi_{\theta_{old}}(O|q)] \frac{1}{|o|}\sum_{t=1}^{|o|} \min \left( \frac{\pi_{\theta}(o_t|q, o_{<t})}{\pi_{\theta_{old}}(o_t|q, o_{<t})}, clip \left( \frac{\pi_{\theta}(o_t|q, o_{<t})}{\pi_{\theta_{old}}(o_t|q, o_{<t})} , 1-\epsilon, 1+\epsilon \right) \right) A_t \]

其中\({\pi}_\theta\)和\(\pi_{\theta_{old}}\)分别为当前和旧策略模型，\(q\)、\(o\)分别为问题数据集和旧策略\(\pi_{\theta_{old}}\)中采样的问题和输出，\(\epsilon\)为PPO中引入的用于稳定训练的剪裁相关超参数。\({A_t}\)是优势，它是通过应用广义优势估计GAE计算的。

使用PPO来更新模型参数，\(\pi_{\theta_{old}}\)指的是未更新参数前的的模型，\({\pi}_\theta\)指的是每一步更新后的模型。\(\mathbb{E}[q \sim P(Q), o \sim \pi_{\theta_{old}}(O|q)]\)​可以理解为采样过程。后面那部分是非常常规的PPO算法。而对于优势函数\(A_t\)的计算，有如下计算公式。

\[A_t^{\text{GAE}(\gamma, \lambda)} = \sum_{l=0}^{\infty} (\gamma \lambda)^l \left( r_{t+l} + \gamma V(s_{t+l+1}) - V(s_{t+l}) \right) \]

\(\gamma\) 是折扣因子，\(\lambda\)是\(GAE\)的超参数，\(r_t\)是时间步 \(t\)的奖励，\(V(s_t)\)是状态 \(s_t\)​的价值函数估计，而这个价值模型的体量一般与要训练的策略模型也就是LLM相当。

而\(r_t\)的计算公式如下：

\[r_t = r_\phi (q, o_{\leq t}) - \beta \log \frac{\pi_\theta (o_t | q, o_{< t})}{\pi_{ref}(o_t | q, o_{< t})} \]

\(r_\phi (q, o_{\leq t})\)是专门训练的奖励模型给出的，而\(\beta \log \frac{\pi_\theta (o_t | q, o_{< t})}{\pi_{ref}(o_t | q, o_{< t})}\)则是对每一次奖励都计算一次KL散度进行约束。也就是说每个token生成都要计算一次KL散度。

综上，我们可以看出PPO算法在计算过程中有两个模型要训练，也就是之前提到的Actor网络和Critic网络，也就是LLM与V网络。然后在每个token生成的时候都需要计算KL散度比较浪费资源。GRPO针对这两个问题进行了优化。

GRPO过程

\(V\)函数的作用就是在计算优势函数\(A_t\)时是为了降低方差而被当做baseline，但是LLM的奖励模型的性质就决定了它只会为每个回答\(o\)的最后一个token分配奖励\(r\)而其余的token的奖励都是0，就是因为这个性质，我们很难在每个token处训练出准确的价值函数。

基于这个思想，GRPO决定不用\(V\)函数，而是在旧策略$ \pi_{\theta_{old}}$中采样多个输出，将输出的奖励平均值作为baseline来降低方差。

优化目标：

\[\begin{align*} \mathcal{J}_{GRPO}(\theta) &= \mathbb{E}[q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{old}}(O|q)] \\ &\frac{1}{G} \sum_{i=1}^G \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left\{ \min \left[ \frac{\pi_{\theta}(o_{i,t}|q, o_{i,<t})}{\pi_{\theta, id}(o_{i,t}|q, o_{i,<t})} \hat{A}_{i,t}, \text{clip} \left( \frac{\pi_{\theta}(o_{i,t}|q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q, o_{i,<t})}, 1 - \epsilon, 1 + \epsilon \right) \hat{A}_{i,t} \right] - \beta \mathbb{D}_{KL} \left[ \pi_{\theta} \| \pi_{ref} \right] \right\} \end{align*} \]

其中，\(\epsilon\) 和 \(\beta\) 是超参数，\(\hat{A}_{i,t}\) 是基于每个组内的相对回报计算的优势。GRPO 利用组相对方式计算优势，这与奖励模型的性质很吻合，因为奖励模型通常基于同一问题的输出比较的数据集进行训练。而KL散度也不再是添加到奖励函数里面了，而是直接添加在损失函数上，降低了优势函数\(\hat{A}_{i,t}\)计算的复杂性。

其中

\[\mathbb{D}_{KL}[\pi_{\theta}||\pi_{ref}]=\frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}-\log\frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}-1 \]

与传统的KL散度计算方法不同，这里采用了无偏估计，使计算出来的惩罚项每一次都是正的。

其中\(\hat{A}_{i,t}\)计算方法如下：

\[\hat{A}_{i,t} = r_i - \frac{r_i - \text{mean}(r)}{\text{std}(r)} \]

相对于PPO来说精简了非常多，为了保证训练的稳定性，加了一个标准化。

GRPO的完整算法流程如下：

其中可以看到\(\pi_{ref}\)是最初的模型，在不会有变化，每次模型的变化都不能与\(\pi_{ref}\)​差别过大，保证输出的质量。

总结

回顾开头给出的图片，黄色的是需要训练过程中更新参数的模型，蓝色的是不需要更新参数的模型，GRPO算法相对于PPO算法少训练了一个价值模型，而且大大简化了优势函数的计算，节约了计算资源。