斜率优化入门 例题： Product Sum

问题分析

题目链接：https://codeforces.com/problemset/problem/631/E

本题题意是给定一个长度为 \(N\) 的序列\(a\)，你必须执行一次操作：选择任意一个元素从该序列中取出，接下来在这个序列中选择一个位置重新插入这个元素，使得\(\sum a_i*i\)最大

初步思路

那么可以想到最朴素的一种做法：

令\(Δ\)为操作后 \(\sum a_i*i\) 的变化量，我们计算操作所带来的变化量\(Δ\)的最大值\(Δ_{max}\)，最终结果为 \(\sum a_i*i + Δ_{max}\)，枚举\(L\)，\(R\)，考虑两种方案：

第一种是把 \(a_L\) 放到第 \(R\) 个位置上，对于这种方案，令 \(sum\) 为 \(a\) 数组的前缀和，则可得：

\(Δ = a_L*(R - L) - (sum_{R} - sum_{L})\)

第二种是把 \(a_R\) 放到第L个位置上，对于这种方案，同上易得：

\(Δ = - a_R*(R - L) + (sum_{R - 1} - sum_{L - 1})\)

直接枚举 \(L\)，\(R\) 的複杂度会超时，以第一种方案举例，我们枚举\(a_L\)，思考如何加速找最优的 \(R\)的过程 ，那么这里就可以引入一个算法：斜率优化！

斜率优化的原理

因爲第一种和第二种方案其实处理方式是一模一样的，所以这里我用第一种举例，枚举\(a_L\)，利用斜率优化找到最优的\(R\)：

首先我们观察式子： \(Δ = a_L*(R - L) - (sum_{R} - sum_{L})\)

我们枚举的是\(L\)，那么只与\(L\)有关的项就是定值，我们把他们写在一起就可以得到：\(Δ = (a_L*R - sum_R) + ( sum_L-a_L * L)\)

这个式子中右边括号内的量都是定值，所以我们只要左边括号的式子取最大值就行，我们设左边的式子为 \(temp\) ，现在要求 \(temp\) 的最大值

重点来了： 如果説我们以 \(R\) 为横坐标 \(x\) ，\(sum_R\) 为纵坐标 \(y\)，建立一个平面直角坐标系，我们可以惊喜的发现：

​ $- temp = sum_R - a_L * R $

这与直綫解析式是同构的：
$b=y-k*x $

求 \(temp\) 的最大值，即求 \(-temp\) 的最小值，即求 \(b\) 的最小值，问题被转换成了求直綫 \(y\) 轴上截距的最小值，而这条直綫的斜率 \(k\) 是定值 \(a_L\) ，并且这个直綫需要经过点$(R，sum_R) $

我们从x轴下方无穷远处向上移动一条斜率为 \(a_L\) 的直綫，对于这个直观的问题，很容易想到儅上移中碰到第一个点$(R，sum_R) $时，这条直綫满足要求，且截距最小。

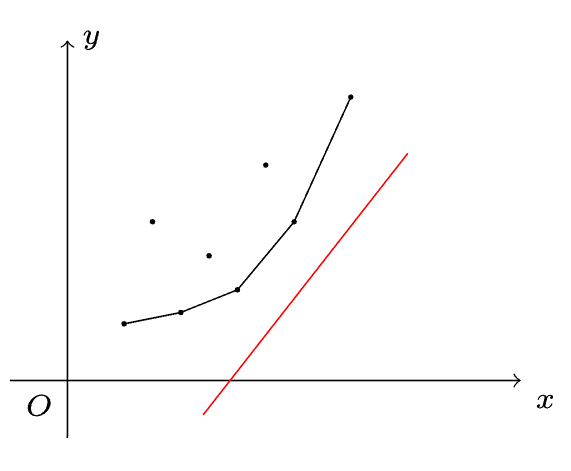
那么碰到的第一个点在哪里呢？我们对所有的 $(R，sum_R) $ 维护一个下凸包，即图中的黑色折綫，第一个点显然在下凸包里，根据下凸包的性质，下凸包的边，从左往右斜率依次递增，所以可以二分，我们二分出斜率最接近直线斜率的那条凸壳边，它的端点就是最优决策点。

斜率优化的实现

注：一般我们都用下凸包和正数的斜率解决最小值问题，对应的，上凸包和负数斜率可以解决最大值问题，但是我们也可以通过给所求式子，\(x\) 和 \(y\) 加上负号，让题目又变成用下凸包和正数的斜率解决最小值问题，上方题目就有这个操作：

​ \(- temp = - (a_L*R - sum_R ) = sum_R - a_L * R\)

1. 问题的转化：

   首先我们要把需要求的最值转化成 \(b=y-k*x\) 的形式，通常情况下都是 \(dp_i =min(y_j - k_i * x_j) + const_i\) ，从 \(i\) 转移到 \(j\) ，其中 \(const_i\) ， \(k_i\) 表示只与 \(i\) 有关的常量 ，\(x_j\) 和 \(y_j\) 表示只与 \(j\) 有关的式子，这个转移需要满足: 式子中和 \(j\) 有关的常量，一个只与 \(j\) 有关，另一个的係数由 \(i\) 决定，这样，我们可以让前者作爲 $ y$ 坐标，后者作爲 \(x\) 坐标，建立平面直角坐标系，用斜率优化解决问题。

2. 下凸包的维护：

   考虑到下凸包的性质，斜率递增，且两个相邻点 \(a\) ，\(b\) 之间没有点 \(c\) 满足 \(k_{ab} > k_{ac}\) 且 \(k _{cb} > k_{ab}\) 。

   看下图的例子，儅已经往下凸包中添加了 \(A\)， \(B\)， \(C_1\) 三个点之后， 拿到一个新点 \(C_2\) ，此时需要判断直綫 \(BC_1\) 和 直綫\(BC_2\) 的斜率谁更小，如果后者更小，那么进行回退，我们把 \(C_1\) 点删除 ，继续刚刚的判断过程，发现需要继续回退，于是把 \(B\) 点也删除， 最后把 \(C_2\) 加入。

   因爲需要反复删除和添加点来维护下凸包这个点集，所以我们一般使用单调队列或单调栈来作爲下凸包的载体。

3. 在下凸包中二分的实现：

   根据下凸包的性质，下凸包的边，从左往右斜率依次递增，所以可以二分，我们二分出斜率最接近直线斜率的那条凸壳边的右端点，即最优决策点。

关于下凸包的维护和操作，详见代码。

后记

异曲同工的算法 ------- CHT（凸包优化）：https://luckyglass.github.io/2019/19Dec21stArt1/

关于凸包的维护，考虑 \(x\) 不按升序给出， 我们需要用到李超树：https://oi-wiki.org/ds/li-chao-tree/

AC_Code

• C++

#include<iostream>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<cstring>
#include<set>
#include<queue>
#include<iomanip>
#include <functional>
#define eol "\n"
typedef long long ll;
typedef unsigned long long ull;
const int inf = 0x3f3f3f3f;
const int mod = 998244353;
const int N   = 1E6 + 7;
using namespace std;
ll ksm(ll v,ll b) {ll res=1;v%=mod; while(b){if(b&1)res=res*v%mod;b>>=1;v=v*v%mod;}return res%mod;}
ll gcd(ll v,ll b) {return b==0?v:gcd(b,v%b);}
ll lcm(ll v,ll b) {return v/gcd(v,b)*b;}
ll inv(ll x) {return ksm(x, mod-2);}

struct Convex_Hull
{
    int sz;
    pair<long long,long long> line[N];
    void init()//初始化
    {
        memset(line,0,sizeof(line));
        sz=0;
    }
    long long get(int p,long long x)//计算在p点的直线的截距
    {
        return line[p].first*x+line[p].second;
    }
    bool is_bad(long long x,long long y,long long z)//判断当前点和新加入的点那个更优
    {
        long long fi = (line[x].second-line[z].second)*(line[x].first-line[y].first);//当前边的斜率
        long long se = (line[y].second-line[x].second)*(line[z].first-line[x].first);//新边的斜率
        return fi<=se;//如果新边的斜率更小，那么新的点更优
    }
    void add(long long x,long long y)
    {
        line[sz++]=make_pair(x,y);
        while(sz>2&&is_bad(sz-2,sz-3,sz-1))//新点更优时，上一个点要被舍弃
            line[sz-2]=line[sz-1],sz--;
    }
    long long query(long long x)//二分查找最接近当前斜率的凸包边
    {
        int l = -1 ,r = sz-1;
        while(r-l>1)
        {
            int mid = (l+r)/2;
            if(get(mid,x)<=get(mid+1,x))l=mid;
            else r=mid;
        }
        return get(r,x);
    }
}H;

void solve(){
    int n;cin>>n;
    vector<ll>v(n+1),sum(n+1);
    vector<ll>q(n+1),y(n+1);
    ll ans=0,delta=0,cnt=0;
    for(int i=1;i<=n;i++) cin>>v[i],ans+=v[i]*i,sum[i]=sum[i-1]+v[i];
    H.init();
    for(int i=2;i<=n;i++)
    {
        H.add(i-1,-sum[i-2]);
        delta=max(delta,H.query(v[i])+sum[i-1]-v[i]*i);
    }
    H.init();
    for(int i=n-1;i>=1;i--)
    {
        H.add(-(i+1),-sum[i+1]);
        delta=max(delta,H.query(-v[i])+sum[i]-v[i]*i);
    }
    cout<<ans+delta<<'\n';
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    int t = 1; //cin>>t;
    while (t--) solve();
}