知识点1：DDPM数学原理

注1：本文系"视觉方向大厂面试·硬核通关"专栏文章。本专栏致力于对多模态大模型/CV领域的高频高难面试题进行深度拆解。本期攻克的难题是：DDPM（去噪扩散概率模型）的数学原理与推导。

注2：关注公众号，每天一道有深度的面试题

---

知识点1：DDPM数学原理

一、面试原题复现

面试官提问：请从数学原理出发，完整推导DDPM的变分下界（ELBO）推导过程，并解释为何可以将训练目标简化为预测噪声。同时，手写DDPM的核心训练代码实现，并分析其与Score-Based生成模型的本质联系。

---

二、关键回答（The Hook）

DDPM的本质是将生成建模问题转化为马尔可夫链的逆向过程学习。通过固定前向扩散过程（向数据逐步添加高斯噪声直到变为纯噪声），并学习一个参数化的反向过程（逐步去除噪声以重建数据）。其数学核心在于变分推断框架：通过最大化证据下界（ELBO）来逼近真实数据分布的对数似然。关键洞察在于，当反向过程也采用高斯分布时，KL散度具有闭式解，从而将复杂的概率推断问题简化为预测噪声的回归问题。这一简化不仅降低了计算复杂度，更建立了扩散模型与Score-Based生成模型的等价性，为后续的Stable Diffusion等大规模生成模型奠定了理论基础。

---

三、深度原理解析（The Meat）

3.1 前向扩散过程的数学建模

前向扩散过程是一个固定的马尔可夫链，逐步向数据添加高斯噪声。设原始数据为$\mathbf{x}_0 \sim q(\mathbf{x}_0)$，前向过程定义为：

$$q(\mathbf{x}_{1:T}|\mathbf{x}0) = \prod^{T} q(\mathbf{x}t|\mathbf{x})$$

其中单步转移分布为：
$$q(\mathbf{x}t|\mathbf{x}) = \mathcal{N}(\mathbf{x}t; \sqrt{1-\beta_t}\mathbf{x}, \beta_t\mathbf{I})$$

这里$\beta_t \in (0,1)$是预定义的噪声调度参数，控制每步添加噪声的强度。

关键性质：任意时间步的直接采样

由于每步添加的噪声是独立的高斯分布，我们可以通过重参数化技巧直接从$\mathbf{x}_0$采样任意时间步的$\mathbf{x}_t$，而无需递归计算。定义：
$$\alpha_t = 1 - \beta_t, \quad \bar{\alpha}t = \prod^{t} \alpha_s$$

则有：
$$q(\mathbf{x}_t|\mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t}\mathbf{x}_0, (1-\bar{\alpha}_t)\mathbf{I})$$

重参数化形式为：
$$\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$$

物理含义：$\sqrt{\bar{\alpha}_t}$表示原始信号的保留比例，$\sqrt{1-\bar{\alpha}_t}$表示注入噪声的比例。当$t \to T$时，$\bar{\alpha}_t \to 0$，因此$\mathbf{x}_T \to \mathcal{N}(\mathbf{0}, \mathbf{I})$，即变为纯高斯噪声。

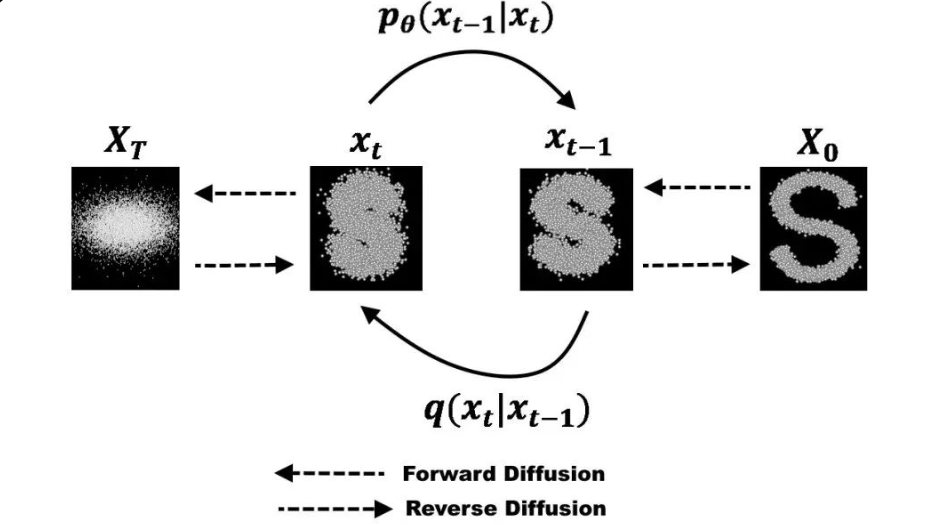
面试官追问：为何选择$\beta_t$线性递增的调度策略？这会对训练过程产生什么影响？

避坑指南：线性调度（$\beta_t$从$\beta_1=10^{-4}$线性增长到$\beta_T=0.02$）确保了早期步保留较多信号信息，后期步充分探索噪声空间。若$\beta_t$增长过快，会导致早期信息丢失严重；若过慢，则需要更多步数才能达到纯噪声状态。实践中也有采用余弦调度的改进策略。

3.2 反向过程与变分推断框架

反向过程的目标是学习一个参数化的马尔可夫链，从纯噪声$\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$逐步去噪至真实数据分布：

$$p_\theta(\mathbf{x}{0:T}) = p(\mathbf{x}T) \prod^{T} p\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)$$

其中单步反向转移分布假设为高斯分布：
$$p_\theta(\mathbf{x}{t-1}|\mathbf{x}t) = \mathcal{N}(\mathbf{x}; \boldsymbol{\mu}\theta(\mathbf{x}t, t), \boldsymbol{\Sigma}\theta(\mathbf{x}_t, t))$$

训练目标：最大化数据的对数似然$\log p_\theta(\mathbf{x}_0)$。由于直接计算不可行，通过引入前向过程作为变分后验，利用Jensen不等式构造证据下界（ELBO）：

$$
\log p_\theta(\mathbf{x}0) \geq \mathbb{E}{1:T}|\mathbf{x}0)} \left[ \log \frac{p\theta(\mathbf{x})}{q(\mathbf{x}_{1:T}|\mathbf{x}0)} \right] =: \mathcal{L}{\text{VLB}}
$$

3.3 ELBO的展开与分解

展开ELBO表达式：

$$\mathcal{L}{\text{VLB}} = \mathbb{E}q \left[ \log p\theta(\mathbf{x}T) + \sum^{T} \log p\theta(\mathbf{x}_{t-1}|\mathbf{x}t) - \sum^{T} \log q(\mathbf{x}t|\mathbf{x}) \right]$$

利用马尔可夫性质和条件概率的定义，可以重写为：

$$\mathcal{L}_{\text{VLB}} = \mathbb{E}q \left[ \log \frac{p\theta(\mathbf{x}T)}{q(\mathbf{x}T|\mathbf{x}0)} + \sum^{T} \log \frac{p\theta(\mathbf{x}|\mathbf{x}t)}{q(\mathbf{x}|\mathbf{x}_t, \mathbf{x}0)} + \log p\theta(\mathbf{x}_0|\mathbf{x}_1) \right]$$

识别出KL散度的形式：$\log \frac{p}{q} = -\log \frac{q}{p}$，因此：

$$\mathcal{L}{\text{VLB}} = \mathbb{E}q \left[ \underbrace{D{\text{KL}}(q(\mathbf{x}T|\mathbf{x}0) | p(\mathbf{x}T))} + \sum^{T} \underbrace{D{\text{KL}}(q(\mathbf{x}|\mathbf{x}t, \mathbf{x}0) | p\theta(\mathbf{x}|\mathbf{x}t))}{L_{t-1}} - \underbrace{\log p_\theta(\mathbf{x}_0|\mathbf{x}1)} \right]$$

各项解释：

• $L_T$：前向过程最终分布与先验分布的差异，由于两者都是固定的高斯分布，该项为常数，可忽略
• $L_{t-1}$（$t=2,\ldots,T$）：去噪项，衡量真实后验与近似反向过程的差异
• $L_0$：重建项，衡量从$\mathbf{x}_1$重建$\mathbf{x}_0$的质量

3.4 后验分布$q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)$的闭式解

这是DDPM数学推导的关键步骤。利用贝叶斯公式：

$$q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) = \frac{q(\mathbf{x}t|\mathbf{x}, \mathbf{x}0) q(\mathbf{x}|\mathbf{x}_0)}{q(\mathbf{x}_t|\mathbf{x}_0)}$$

由于马尔可夫性质，$q(\mathbf{x}t|\mathbf{x}, \mathbf{x}_0) = q(\mathbf{x}t|\mathbf{x})$。三个高斯分布的比值仍为高斯分布：

$$q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}0) = \mathcal{N}(\mathbf{x}; \tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t\mathbf{I})$$

其中均值和方差为：
$$\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}0) = \frac{\sqrt{\alpha_t}(1-\bar{\alpha})}{1-\bar{\alpha}_t}\mathbf{x}t + \frac{\sqrt{\bar{\alpha}{t-1}}\beta_t}{1-\bar{\alpha}_t}\mathbf{x}_0$$

$$\tilde{\beta}t = \frac{1-\bar{\alpha}{t-1}}{1-\bar{\alpha}_t}\beta_t$$

关键洞察：后验均值是$\mathbf{x}_t$和$\mathbf{x}_0$的线性组合，这意味着如果我们能准确预测$\mathbf{x}_0$，就能计算出最优的去噪均值。

3.5 从均值预测到噪声预测的转换

由于$\mathbf{x}_0 = \frac{\mathbf{x}_t - \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}}{\sqrt{\bar{\alpha}_t}}$，可以将后验均值重写为关于噪声$\boldsymbol{\epsilon}$的函数：

$$\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon} \right)$$

现在，我们让神经网络$\boldsymbol{\epsilon}_\theta(\mathbf{x}t, t)$来预测噪声$\boldsymbol{\epsilon}$，而非直接预测均值$\boldsymbol{\mu}\theta(\mathbf{x}_t, t)$。参数化反向过程为：

$$p_\theta(\mathbf{x}{t-1}|\mathbf{x}t) = \mathcal{N}(\mathbf{x}; \boldsymbol{\mu}\theta(\mathbf{x}t, t), \boldsymbol{\Sigma}\theta(\mathbf{x}_t, t))$$

其中：
$$\boldsymbol{\mu}_\theta(\mathbf{x}_t, t) = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}t}}\boldsymbol{\epsilon}\theta(\mathbf{x}_t, t) \right)$$

方差$\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)$可以固定为$\tilde{\beta}_t\mathbf{I}$或$\beta_t\mathbf{I}$（论文实验表明两者性能接近）。

3.6 损失函数的简化

由于两个高斯分布的KL散度有闭式解：

$$D_{\text{KL}}(\mathcal{N}(\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1) | \mathcal{N}(\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2)) = \frac{1}{2} \left[ \text{tr}(\boldsymbol{\Sigma}_2^{-1}\boldsymbol{\Sigma}_1) + (\boldsymbol{\mu}_2 - \boldsymbol{\mu}_1)^T \boldsymbol{\Sigma}_2^{-1}(\boldsymbol{\mu}_2 - \boldsymbol{\mu}_1) + \log \frac{|\boldsymbol{\Sigma}_2|}{|\boldsymbol{\Sigma}_1|} - d \right]$$

当协方差矩阵相等时，简化为：
$$D_{\text{KL}} = \frac{1}{2\sigma^2} |\boldsymbol{\mu}_1 - \boldsymbol{\mu}_2|^2$$

应用于DDPM的去噪项：
$$L_{t-1} = \mathbb{E}_q \left[ \frac{1}{2\tilde{\beta}t} |\boldsymbol{\mu}\theta(\mathbf{x}_t, t) - \tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)|^2 \right] + C$$

代入均值表达式并消去常数项后：
$$L_{t-1} = \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}, t} \left[ \frac{\beta_t^2}{2\tilde{\beta}_t\alpha_t(1-\bar{\alpha}t)} |\boldsymbol{\epsilon} - \boldsymbol{\epsilon}\theta(\mathbf{x}_t, t)|^2 \right]$$

其中$\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}$。

Ho et al. (2020)的关键简化：忽略权重项$\frac{\beta_t^2}{2\tilde{\beta}_t\alpha_t(1-\bar{\alpha}_t)}$，直接使用均方误差：

$$\mathcal{L}{\text{simple}} = \mathbb{E}0, \boldsymbol{\epsilon}} \left[ |\boldsymbol{\epsilon} - \boldsymbol{\epsilon}\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}, t)|^2 \right]$$

其中$t \sim \mathcal{U}(1, T)$。

面试官追问：为何可以忽略权重项？这对训练过程有什么影响？

避坑指南：忽略权重项在理论上是次优的，但在实践中效果更好。原因在于：权重项在早期噪声水平高时给予的权重较小，而实际上早期步的去噪对最终生成质量至关重要。简化后的目标相当于对噪声水平进行了加权，更强调高噪声水平的步数。实验表明，这种加权策略能产生更高质量的样本。

3.7 与Score-Based模型的等价性

扩散模型与Score-Based生成模型存在深刻的理论联系。回顾Score Matching的目标：

$$\mathbb{E}_{q_t(\mathbf{x}t)} \left[ | \nabla_t} \log q_t(\mathbf{x}t) - \mathbf{s}\theta(\mathbf{x}_t, t) |^2 \right]$$

其中$\mathbf{s}_\theta(\mathbf{x}t, t)$是神经网络，用于估计分数函数$\nabla_t} \log q_t(\mathbf{x}_t)$。

通过推导可以证明，当$\mathbf{s}_\theta(\mathbf{x}_t, t) = -\frac{1}{\sqrt{1-\bar{\alpha}t}}\boldsymbol{\epsilon}\theta(\mathbf{x}_t, t)$时，DDPM的简化损失与Score Matching目标等价：

$$|\boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\mathbf{x}t, t)|^2 \propto | \nabla_t} \log q_t(\mathbf{x}_t) + \frac{1}{\sqrt{1-\bar{\alpha}t}}\boldsymbol{\epsilon}\theta(\mathbf{x}_t, t) |^2$$

几何含义：分数函数$\nabla_{\mathbf{x}_t} \log q_t(\mathbf{x}_t)$指向数据密度增长最快的方向。通过学习预测噪声，实际上是在学习估计分数函数，从而指导随机过程（如Langevin动力学）从噪声分布采样至数据分布。

面试官追问：DDPM、DDIM和Score-Based模型在采样策略上有什么本质区别？

避坑指南：DDPM采用随机采样策略，每步添加新的随机噪声，对应于随机微分方程（SDE）的离散化；DDIM（Denoising Diffusion Implicit Models）采用确定性采样，不添加新噪声，对应于常微分方程（ODE）的离散化，采样速度更快；Score-Based模型通常使用Langevin动力学进行采样。三种方法在连续时间极限下可以统一到同一个随机微分方程框架下。

---

四、代码手撕环节（Live Coding）

4.1 核心训练代码实现

以下提供符合工业界规范的DDPM核心实现：

import torch
import torch.nn as nn
import torch.nn.functional as F
from typing import Optional, Tuple

class GaussianDiffusion:
    """
    DDPM的高斯扩散过程实现
    
    核心功能：
    1. 定义噪声调度（beta schedule）
    2. 计算前向过程和反向过程的分布参数
    3. 计算简化的训练损失
    4. 实现采样过程
    """
    
    def __init__(
        self,
        num_timesteps: int = 1000,
        beta_start: float = 0.0001,
        beta_end: float = 0.02,
        device: str = 'cuda'
    ):
        self.num_timesteps = num_timesteps
        self.device = device
        
        # 定义beta schedule（线性调度）
        self.betas = torch.linspace(beta_start, beta_end, num_timesteps, device=device)
        
        # 计算alpha和alpha_bar
        self.alphas = 1.0 - self.betas
        self.alphas_cumprod = torch.cumprod(self.alphas, dim=0)
        self.alphas_cumprod_prev = F.pad(self.alphas_cumprod[:-1], (1, 0), value=1.0)
        
        # 计算采样过程中的关键参数
        self.sqrt_alphas_cumprod = torch.sqrt(self.alphas_cumprod)
        self.sqrt_one_minus_alphas_cumprod = torch.sqrt(1.0 - self.alphas_cumprod)
        
        # 后验方差（用于反向过程）
        self.posterior_variance = (
            self.betas * (1.0 - self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
        )
        
        # 计算后验均值系数
        self.posterior_mean_coef1 = self.betas * torch.sqrt(self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
        self.posterior_mean_coef2 = (1.0 - self.alphas_cumprod_prev) * torch.sqrt(self.alphas) / (1.0 - self.alphas_cumprod)
    
    def q_sample(
        self,
        x_start: torch.Tensor,
        t: torch.Tensor,
        noise: Optional[torch.Tensor] = None
    ) -> torch.Tensor:
        """
        前向过程：从x_0采样x_t
        
        公式：x_t = sqrt(alpha_bar_t) * x_0 + sqrt(1 - alpha_bar_t) * epsilon
        """
        if noise is None:
            noise = torch.randn_like(x_start)
        
        sqrt_alphas_cumprod_t = self._extract(self.sqrt_alphas_cumprod, t, x_start.shape)
        sqrt_one_minus_alphas_cumprod_t = self._extract(
            self.sqrt_one_minus_alphas_cumprod, t, x_start.shape
        )
        
        return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
    
    def p_losses(
        self,
        denoise_model: nn.Module,
        x_start: torch.Tensor,
        t: torch.Tensor,
        noise: Optional[torch.Tensor] = None,
        loss_type: str = "mse"
    ) -> torch.Tensor:
        """
        计算简化训练损失
        
        公式：L_simple = E[||epsilon - epsilon_theta(x_t, t)||^2]
        """
        if noise is None:
            noise = torch.randn_like(x_start)
        
        # 前向过程：采样x_t
        x_t = self.q_sample(x_start, t, noise)
        
        # 神经网络预测噪声
        predicted_noise = denoise_model(x_t, t)
        
        # 计算损失
        if loss_type == "mse":
            loss = F.mse_loss(predicted_noise, noise)
        elif loss_type == "l1":
            loss = F.l1_loss(predicted_noise, noise)
        else:
            raise NotImplementedError(f"Unknown loss type: {loss_type}")
        
        return loss
    
    def p_mean_variance(
        self,
        denoise_model: nn.Module,
        x_t: torch.Tensor,
        t: torch.Tensor
    ) -> Tuple[torch.Tensor, torch.Tensor]:
        """
        计算反向过程p(x_{t-1}|x_t)的均值和方差
        """
        # 预测噪声
        predicted_noise = denoise_model(x_t, t)
        
        # 计算均值
        alpha_t = self._extract(self.alphas, t, x_t.shape)
        alpha_bar_t = self._extract(self.alphas_cumprod, t, x_t.shape)
        beta_t = self._extract(self.betas, t, x_t.shape)
        sqrt_one_minus_alpha_bar_t = self._extract(self.sqrt_one_minus_alphas_cumprod, t, x_t.shape)
        
        # 公式：mu_theta = (x_t - beta_t/sqrt(1-alpha_bar_t) * epsilon_theta) / sqrt(alpha_t)
        mean = (x_t - beta_t / sqrt_one_minus_alpha_bar_t * predicted_noise) / torch.sqrt(alpha_t)
        
        # 计算方差（使用后验方差）
        variance = self._extract(self.posterior_variance, t, x_t.shape)
        
        return mean, variance
    
    def p_sample(
        self,
        denoise_model: nn.Module,
        x_t: torch.Tensor,
        t: torch.Tensor
    ) -> torch.Tensor:
        """
        单步反向采样：从x_t采样x_{t-1}
        """
        mean, variance = self.p_mean_variance(denoise_model, x_t, t)
        noise = torch.randn_like(x_t)
        
        # 当t=0时，不添加噪声
        nonzero_mask = ((t != 0).float().view(-1, *([1] * (len(x_t.shape) - 1))))
        
        return mean + nonzero_mask * torch.sqrt(variance) * noise
    
    def p_sample_loop(
        self,
        denoise_model: nn.Module,
        shape: Tuple[int, ...]
    ) -> torch.Tensor:
        """
        完整采样循环：从x_T采样到x_0
        """
        # 从纯噪声开始
        x_t = torch.randn(shape, device=self.device)
        
        for i in reversed(range(self.num_timesteps)):
            t = torch.full((shape[0],), i, device=self.device, dtype=torch.long)
            x_t = self.p_sample(denoise_model, x_t, t)
        
        return x_t
    
    @staticmethod
    def _extract(
        a: torch.Tensor,
        t: torch.Tensor,
        x_shape: Tuple[int, ...]
    ) -> torch.Tensor:
        """
        从调度中提取特定时间步的参数，并广播到输入形状
        """
        batch_size = t.shape[0]
        out = a.gather(-1, t)
        return out.reshape(batch_size, *((1,) * (len(x_shape) - 1)))


# 简化的UNet骨干网络（用于演示）
class SimpleUNet(nn.Module):
    """
    简化的UNet实现，用于噪声预测
    实际工程中应使用更复杂的架构（如ResNet块、注意力机制等）
    """
    
    def __init__(
        self,
        in_channels: int = 3,
        model_channels: int = 128,
        num_res_blocks: int = 2,
        attention_resolutions: Tuple[int, ...] = (16,),
        dropout: float = 0.0
    ):
        super().__init__()
        self.in_channels = in_channels
        self.model_channels = model_channels
        
        # 时间嵌入层
        self.time_embed = nn.Sequential(
            nn.Linear(128, model_channels),
            nn.SiLU(),
            nn.Linear(model_channels, model_channels)
        )
        
        # 输入卷积层
        self.input_blocks = nn.ModuleList([
            nn.Conv2d(in_channels, model_channels, kernel_size=3, padding=1)
        ])
        
        # 残差块和注意力层（简化实现）
        self.middle_block = self._make_res_block(model_channels, dropout)
        
        # 输出层
        self.output_blocks = nn.ModuleList([
            nn.Conv2d(model_channels, in_channels, kernel_size=3, padding=1)
        ])
    
    def _make_res_block(
        self,
        channels: int,
        dropout: float
    ) -> nn.Module:
        return nn.Sequential(
            nn.GroupNorm(32, channels),
            nn.SiLU(),
            nn.Conv2d(channels, channels, kernel_size=3, padding=1),
            nn.GroupNorm(32, channels),
            nn.SiLU(),
            nn.Dropout(dropout),
            nn.Conv2d(channels, channels, kernel_size=3, padding=1)
        )
    
    def timestep_embedding(self, timesteps: torch.Tensor, dim: int = 128) -> torch.Tensor:
        """
        正弦位置编码，用于编码时间步信息
        """
        half = dim // 2
        freqs = torch.exp(
            -math.log(10000) * torch.arange(half, dtype=torch.float32) / half
        ).to(device=timesteps.device)
        args = timesteps[:, None].float() * freqs[None]
        embedding = torch.cat([torch.cos(args), torch.sin(args)], dim=-1)
        if dim % 2:
            embedding = torch.cat([embedding, torch.zeros_like(embedding[:, :1])], dim=-1)
        return embedding
    
    def forward(self, x: torch.Tensor, timesteps: torch.Tensor) -> torch.Tensor:
        """
        前向传播：输入x_t和时间步t，输出预测的噪声
        """
        # 时间嵌入
        emb = self.timestep_embedding(timesteps)
        emb = self.time_embed(emb)
        
        # 输入处理
        h = self.input_blocks[0](x)
        
        # 中间处理（简化）
        h = self.middle_block(h)
        
        # 输出
        return self.output_blocks[0](h)


# 训练循环示例
def train_diffusion_model(
    denoise_model: nn.Module,
    diffusion: GaussianDiffusion,
    dataloader: torch.utils.data.DataLoader,
    num_epochs: int = 100,
    lr: float = 1e-4,
    device: str = 'cuda'
):
    """
    DDPM模型的训练循环
    """
    denoise_model = denoise_model.to(device)
    optimizer = torch.optim.AdamW(denoise_model.parameters(), lr=lr)
    
    for epoch in range(num_epochs):
        for batch_idx, (images, _) in enumerate(dataloader):
            images = images.to(device)  # 假设images在[-1, 1]范围
            
            batch_size = images.shape[0]
            
            # 随机采样时间步
            t = torch.randint(0, diffusion.num_timesteps, (batch_size,), device=device)
            
            # 计算损失
            loss = diffusion.p_losses(denoise_model, images, t)
            
            # 反向传播和优化
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            if batch_idx % 100 == 0:
                print(f"Epoch {epoch}, Batch {batch_idx}, Loss: {loss.item():.4f}")
        
        # 定期采样可视化
        if (epoch + 1) % 10 == 0:
            with torch.no_grad():
                samples = diffusion.p_sample_loop(denoise_model, (16, 3, 32, 32))
                # 保存或显示样本（略）
                print(f"Epoch {epoch + 1}: Generated samples")
    
    return denoise_model

4.2 关键实现细节解析

1. 时间嵌入（Time Embedding）

def timestep_embedding(self, timesteps: torch.Tensor, dim: int = 128) -> torch.Tensor:
    half = dim // 2
    freqs = torch.exp(-math.log(10000) * torch.arange(half) / half)
    args = timesteps[:, None].float() * freqs[None]
    embedding = torch.cat([torch.cos(args), torch.sin(args)], dim=-1)
    return embedding

这是Transformer风格的正弦位置编码，用于编码时间步信息。其优势在于：

• 无需学习参数，避免过拟合
• 具有良好的外推性能
• 相对位置关系保持不变

2. EMA（Exponential Moving Average）
在实际工业实现中，通常会维护模型参数的EMA版本：

def update_ema(ema_model, model, decay=0.9999):
    with torch.no_grad():
        for ema_param, param in zip(ema_model.parameters(), model.parameters()):
            ema_param.data.mul_(decay).add_(param.data, alpha=1 - decay)

EMA版本在推理时表现更稳定，是标准做法。

3. 混合精度训练
为加速训练和节省显存，常用混合精度训练：

scaler = torch.cuda.amp.GradScaler()

with torch.cuda.amp.autocast():
    loss = diffusion.p_losses(denoise_model, images, t)

scaler.scale(loss).backward()
scaler.step(optimizer)
scaler.update()

---

五、进阶追问与展望

5.1 常见面试追问

追问1：DDPM与传统生成模型（如GAN、VAE）的本质区别是什么？

回答要点：

• GAN：通过对抗训练学习从噪声到数据的映射，存在模式崩溃（mode collapse）问题，训练不稳定。
• VAE：通过变分推断学习数据的隐变量分布，生成质量受限于近似后验的表达能力。
• DDPM：通过逐步去噪的马尔可夫链生成样本，训练稳定，能覆盖完整的模态，但采样速度较慢。数学上，DDPM与VAE有相似之处（都使用ELBO），但DDPM的隐变量是所有中间状态$\mathbf{x}_{1:T}$，而非单一隐变量。

追问2：如何加速DDPM的采样过程？有哪些SOTA方法？

回答要点：

• DDIM：确定性采样，减少采样步数至50-100步，质量损失较小。
• Progressive Distillation：知识蒸馏，将多步教师模型压缩为少步学生模型。
• Consistency Distillation：一致性蒸馏，保证不同采样步的输出一致。
• Trajectory Segmented Consistency Distillation (TSCD)：分段一致性蒸馏（Hyper-SD方法），在1-8步内达到SOTA性能。
• Score Distillation Sampling (SDS)：在潜空间进行蒸馏，提升采样效率。

追问3：DDPM在多模态生成中的应用（如Stable Diffusion）的关键设计是什么？

回答要点：

• Latent Diffusion：在VAE的潜空间进行扩散，大幅降低计算复杂度。
• Cross-Attention：通过交叉注意力机制注入条件信息（如文本、图像、深度图）。
• ControlNet：添加额外的控制网络，实现精细控制（如边缘、姿态控制）。
• LoRA（Low-Rank Adaptation）：轻量级适配器，实现高效的风格迁移和个性化微调。

5.2 最新SOTA改进方向

1. 采样加速

• E2EDiff：端到端训练框架，直接优化最终重建质量，消除训练-采样差距。
• Trajectory Refinement：轨迹精炼，通过线性外推拟合误差，修正采样轨迹。

2. 质量提升

• Human Feedback Learning：引入人类反馈，优化低步数场景下的生成质量。
• Reflectance-Aware Trajectory Refinement (RATR)：反射感知轨迹精炼，适用于低光图像增强等特定任务。

3. 泛化能力

• Generalized Diffusion Adaptation (GDA)： generalized框架，增强对分布偏移的鲁棒性。
• Effective Conditioning：改进条件注入机制，如ECoDepth使用ViT嵌入增强单目深度估计。

5.3 理论前沿

1. 确定性扩散（Diffusion with Deterministic Policy）
探索确定性采样策略，避免随机噪声引入的不确定性，提升生成可控性。

2. 连续时间扩散模型（Continuous-time Diffusion）
在连续时间框架下研究扩散过程，利用随机微分方程（SDE）和常微分方程（ODE）的等价性，提供更灵活的采样策略。

3. 扩散模型与其他生成模型的统一
探索扩散模型与能量模型（EBM）、流模型之间的理论联系，建立统一的生成模型框架。

---

六、总结与启示

DDPM的成功并非偶然，其数学严谨性与工程可行性达到了完美的平衡。从变分推断的理论框架到噪声预测的工程简化，每一步都有清晰的数学动机和直观的几何解释。

核心方法论：

1. 问题转化：将生成问题转化为去噪问题
2. 框架选择：利用变分推断的ELBO框架
3. 参数化策略：通过噪声预测简化优化目标
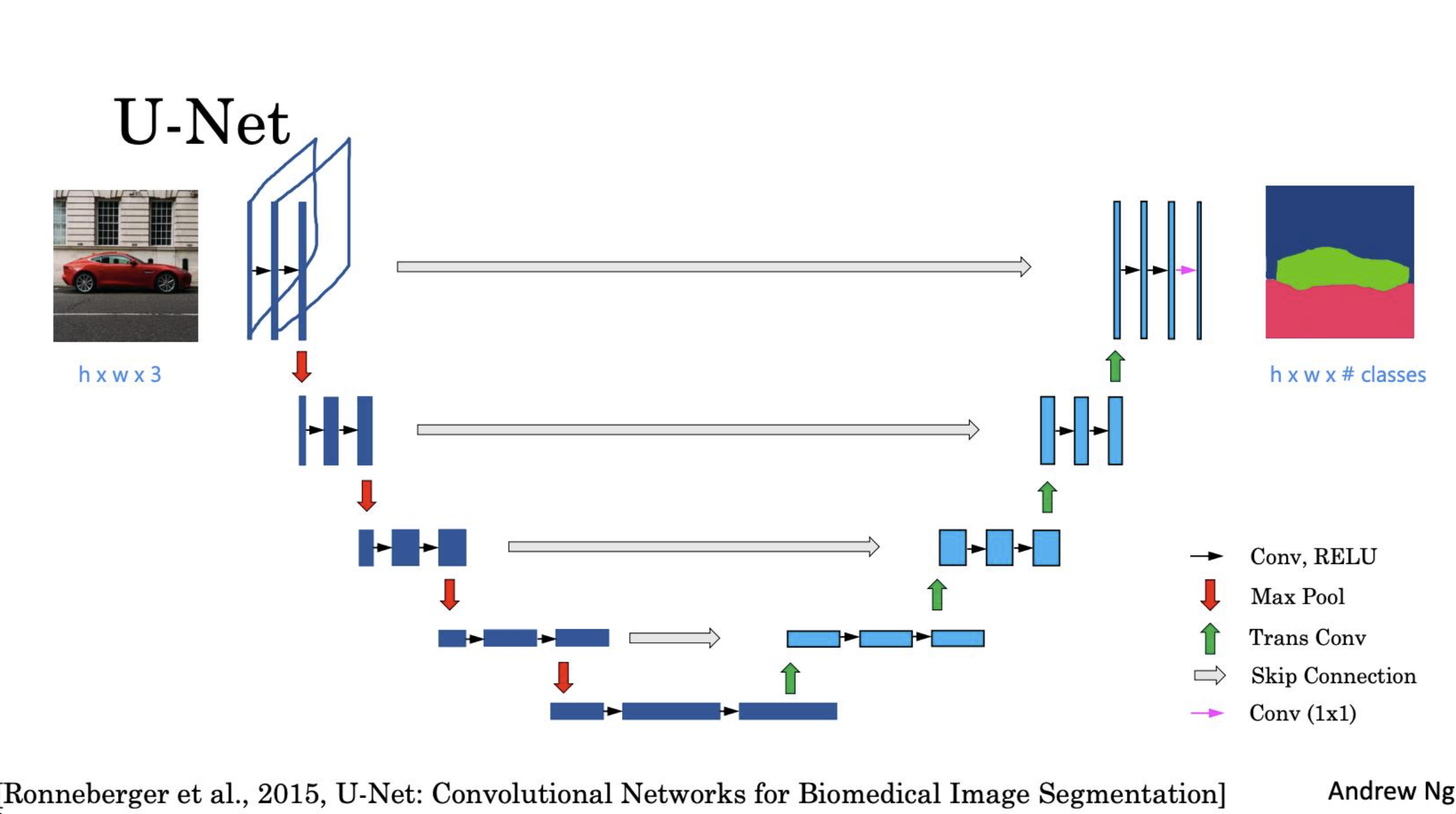
4. 架构设计：U-Net结合时间嵌入，捕获多尺度特征和时间信息

面试准备建议：

• 熟练掌握前向和反向过程的数学推导
• 理解ELBO分解和损失函数简化的原因
• 掌握噪声预测与分数估计的联系
• 了解SOTA加速方法和改进方向
• 能够手写核心训练和采样代码

DDPM不仅是当前生成式AI的核心技术，更是理解多模态大模型、计算成像等领域的基础。深入掌握其数学原理和实现细节，将为面试官展示扎实的理论基础和工程能力。

---

参考文献：

1. Ho, J., Jain, A., & Abbeel, P. (2020). Denoising Diffusion Probabilistic Models.
2. Song, Y., & Ermon, S. (2019). Generative Modeling by Estimating Gradients of the Data Distribution.
3. Song, J., Meng, C., & Ermon, S. (2020). Denoising Diffusion Implicit Models.
4. Salimans, T., & Ho, J. (2022). Progressive Distillation for Fast Sampling of Diffusion Models.
5. Karras, T., et al. (2022). Elucidating the Design Space of Diffusion-Based Generative Models.

---

附录：关键公式速查表

公式名称	表达式	说明
单步前向转移	$q(\mathbf{x}t|\mathbf{x}) = \mathcal{N}(\mathbf{x}t; \sqrt{1-\beta_t}\mathbf{x}, \beta_t\mathbf{I})$	添加高斯噪声
任意步前向采样	$\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}$	重参数化技巧
后验均值	$\tilde{\boldsymbol{\mu}}_t = \frac{1}{\sqrt{\alpha_t}}(\mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon})$	最优去噪方向
网络预测均值	$\boldsymbol{\mu}_\theta = \frac{1}{\sqrt{\alpha_t}}(\mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}t}}\boldsymbol{\epsilon}\theta)$	参数化反向过程
简化损失	$\mathcal{L}{\text{simple}} = \mathbb{E}\left[|\boldsymbol{\epsilon} - \boldsymbol{\epsilon}\theta(\mathbf{x}_t, t)|^2\right]$	实际训练目标