图论-2Sat

2-Sat 入门

引入现实问题

有如下问题解决。

人物	要求一	要求二
小 A	吃芒果	吃桃子
小 B	不吃苹果	不吃葡萄
小 C	吃芒果	不吃桃子
小 D	不吃葡萄	吃桃子

问题：葡萄、苹果、桃子、芒果中，哪几种水果可以满足所有小朋友中的一个要求。
答案：芒果或芒果、桃子、葡萄或其他。

2-Sat 问题就是解决上面的问题的。简单来说，有 \(n\) 个集合，对于每一个集合都有两个元素，某一个集合 \(a_i\) 中一定有一个元素且仅有一个元素会被选择，同时对于这些集合的元素都会有若干个限制（一般会保证不会直接输入一个集合两个元素都选的情况）求对于每一个集合 \(a_i\) 取元素 \(1\) 还是取元素 \(2\)。

大部分题目就会这么出：给出 \(m\) 个如「满足 \(x_i=0/1\) 或 \(x_j=0/1\) 成立」「若 \(x_i=0/1\) 则 \(x_j=0/1\) 成立」等形式的要求，\(0\) 和 \(1\) 就是集合中的两个元素。求任意一种 \(01\) 串满足要求。

上面题目中，每一个小朋友的要求就是限制，即我们上面提到的「满足 \(x_i=0/1\) 或 \(x_j=0/1\) 成立」，每一个水果吃还是不吃组成一个集合。而最后的答案就是 \(01\) 串，吃还是不吃某一种水果。

怎么解？

暴力方法

暴力枚举 \(a_i\) 具体取法，最后再对于每一个要求都判断。

伪代码如下。

dfs(p)
if -> p>n
	return check 
else 
	a[p+1]=1
	if -> dfs(p+1)=1 return 1
	a[p+1]=0
	if -> dfs(p+1)=1 return 1
	return 0

此时复杂度即为 \(O(2^n m)\)，显然超时。

思考一下，上面的代码复杂在哪里？不难发现，当选择了一个值后，之后的有些值就已经确定了。但是这里却要重复计算。

如果给上面优化呢？好像也不行。

到这里，正着枚举似乎不行，不妨从限制条件出发，看看怎么解决。

正确方法

对于这些问题，例如「若 \(x_i=0/1\) 成立则 \(x_j=0/1\) 成立」意思是只有 \(x_i=0/1\) 时，才能访问 \(x_j=0/1\)。

这里我们可以发现上面是具有指向的，所以我们可以建边，对每一个集合的元素 \(x_i=0\) 和 \(x_i=1\) 都建立一个点（此时有 \(2n\) 个点），对于每一个要求，都建立一个有向边，由 \(i\) 号点到 \(j\) 号点的一个边，就表示「若 \(i\) 成立则 \(j\) 成立」。

当然出题人不会直接给你「若 \(x_i=0/1\) 成立则 \(x_j=0/1\) 成立」形式的题目，要不然就没啥意义了，所以一般会将题目转化成「若 \(x_i=0/1\) 成立则 \(x_j=0/1\) 成立」的形式。由于要转化，所以有的出题人会搞一些东西使得你会新建好多条边，做题人就会使出优化建边，但基础题一般不会出现。

例如题目“若第 \(i\) 个元素为 \(a\)，则第 \(j\) 个元素必定为 \(b\)”中样例为下面。

\(1\) \(0\) \(2\) \(0\)

\(2\) \(0\) \(1\) \(1\)

\(2\) \(1\) \(1\) \(0\)

我们可以按照上面画出来图如下。

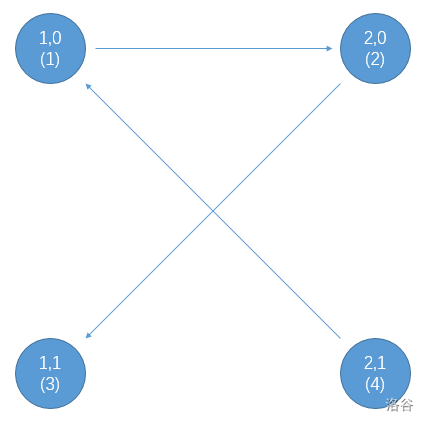
注意此时：若某一个集合中的两个元素对应点是相互可达即是强连通的，说明是不合法的。反之是合法的。所以图中情况是合法的。原因是若强连通，此时可以推出：若第 \(i\) 个元素为 \(a\)，则第 \(i\) 个元素必定为 \(b\) 这种，显然矛盾。

最后，上面图中，每一个点都是联通的，哪一个才是合法的。

从图中我们知道，答案就是图中拓扑序大的，即对于每一个集合都选择拓扑序小的那一个元素。原因在于 \(1 \to 2\to 3\) 中，\(1\) 和 \(3\) 在同一个集合里，因为 \(1,3\) 的拓扑序，可以推出他们的先后顺序，即有 \(1\) 就有 \(3\)，但不代表 \(1\) 就有 \(3\)，所以选择拓扑序较大的。

但但但是，聪明的你会发现，图中有环的时候，就没法拓扑了。所以此时我们需要缩点。这里可以使用并查集或者 Tarjan。

代码如下。

void tarjan(int u)
{
	dfn[u]=low[u]=++tim,st[++top]=u,vis[u]=1;
	for(auto v:e[u])
	{
		if(!dfn[v])
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		scc_sum++;
		while(st[top]!=u) scc[st[top]]=scc_sum,vis[st[top]]=0,top--;
		scc[st[top]]=scc_sum,vis[st[top]]=0,top--;
	}
}


//main里这么写
for(int i=1;i<=2*n;i++) if(!dfn[i])          tarjan(i);
for(int i=1;i<=n;i++)   if(scc[i]==scc[i+n]) return cout<<"IMPOSSIBLE"<<endl,0;
cout<<"POSSIBLE"<<endl;
for(int i=1;i<=n;i++)
{
	if(scc[i]>scc[i+n])  cout<<"1 ";  
	else                 cout<<"0 ";
}

最后 Tarjan 就正好帮我们求出了某一个点在哪一个强连通分量里，输出大的那个就可以。

总结

2-Sat 的问题，基本都是这几个东西：集合、两个元素和条件。

所以遇到 2-Sat 问题，你可以按照以下步骤去完成：

1. 先从题目中找到条件是啥，一般会作为输入。
2. 通过条件找出集合及其两个元素。
3. 将条件转化为「若 \(x_i=0/1\) 成立则 \(x_j=0/1\) 成立」的形式。例如模板题中，要求是「\(x_i=0/1\) 成立或 \(x_j=0/1\) 成立」此时我们就可以转化为两个「若 \(x_i=0/1\) 成立则 \(x_j=0/1\) 成立」的形式，具体可以看看下面。
4. 输出答案。

例题

P4782 【模板】2-SAT

这道题中，要求是两个条件任意一个满足即可。

所以「若 \(x_i=0/1\) 成立或 \(x_j=0/1\) 成立」这个例子中，我们就可以转化成两个「若一个不满足，则另一个必须满足」的形式。但最后对图的处理都是一样的。

cin>>n>>m;
for(int i=1;i<=m;i++)
{
	cin>>a>>x>>b>>y;
	if(x==0&&y==0) add(a+n,b),add(b+n,a);    
	if(x==0&&y==1) add(a+n,b+n),add(b,a);     
	if(x==1&&y==0) add(a,b),add(b+n,a+n); 
	if(x==1&&y==1) add(a,b+n),add(b,a+n);         
}

P4171 满汉全席

这道题的集合就是每一个党派，而两个元素就是代表。

题意为「若 \(a\) 参加则 \(b\) 不参加」的形式，由于这里是不参加，即不成立。所以依旧要转换。题目中要求党派必须有一人，所以可以转换为「若 \(a\) 参加则 \(b\) 的伙伴参加」的形式。

for(int i=1;i<=m;i++)
{
	cin>>a>>b;
	add(a,((b%2==0)?b-1:b+1));
	add(b,((a%2==0)?a-1:a+1));
}

P5782 和平委员会

这道题就比较难了，我们按照上面步骤来做。

首先找元素是啥。这里不是很明确，题目中说每一个材料只能有一种做法，我们可以将其转化为一种材料中某一种做法选还是不选。但是这里就是 4-Sat 了，会有问题。

但是他是 4-Sat 即 \(2^2\) 此时我们就可以把这个大集合按照做法拆分成两个集合，就是一种材料某一种做法选还是不选（似乎读起来很像）再在这两个集合中「“不选汉式做法”成立则“选满式做法”成立」和「“不选满式做法”成立则“选汉式做法”成立」间连边。

刚刚找出了元素，此时集合也明确了，就是每一道菜的做法。

最后问题的连边就和模板题一样了，就是「“不做第一道菜”满足则“做第二道菜”满足」和「“不做第二道菜”满足则“做第一道菜”满足」连边。

完结撒花！

附一下大佬的题单。