时间序列相关的文章（二）

TEMPO: PROMPT-BASED GENERATIVE PRE-TRAINED TRANSFORMER FOR TIME SERIES FORECASTING

框架

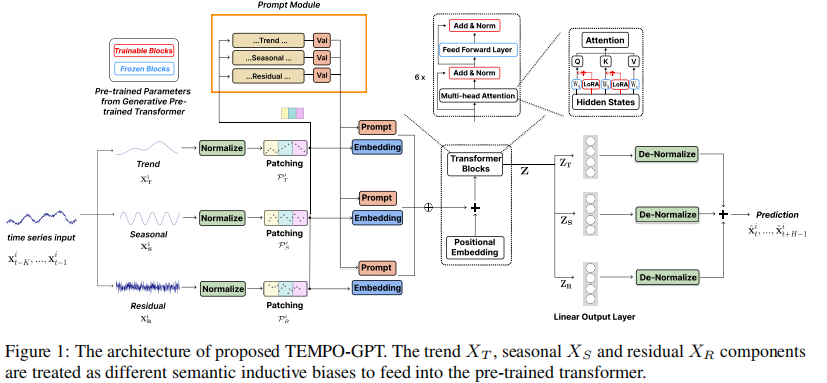
根据您提供的文档和信息，我可以帮助整理出这篇论文的框架及公式说明。以下是简要的内容分解：

1. 时间序列输入表示 (Time Series Input Representation)

在时间序列的表示上，论文使用 STL 分解法将输入序列 $ X \in \mathbb{R}^{n \times L} $ 表示为趋势 (Trend)、季节性 (Seasonality)、和残差 (Residual) 三个主要部分：

\[X^i = X_T^i + X_S^i + X_R^i \]

其中：

$ X_T $ 表示长时间的趋势，使用一个移动平均来计算。
$ X_S $ 表示短时间内的季节性周期。
$ X_R $ 是残差，表示去除趋势和季节性之后的数据。

该分解使得模型能够更有效地提取每个时间序列的不同周期性特征。

2. 提示设计 (Prompt Design)

提示的设计结合了不同时间序列成分的信息，以引导模型进行预测。这种设计通过将不同成分的特定提示嵌入进行整合，有助于模型更好地理解各成分之间的关系。

提示设计的表达形式为：

\[x_T = [V_t; P_T] \]

其中，( V_t ) 是用于趋势的提示，( P_T ) 是可学习的提示向量，用于控制和适应不同的时间序列任务。

3. 生成预训练的 Transformer 架构 (Generative Pre-trained Transformer Architecture)

论文选择基于生成式预训练 Transformer (GPT) 作为时间序列预测的主干网络，模型的输入是各个分解后的成分，最终输出为三个分量的预测值：

\[x = x_T \oplus x_S \oplus x_R \]

在模型内使用了 LORA（Low-Rank Adaptation）来适应不同的时间序列分布，这样可以在保持较少参数的前提下，进行有效的时间序列适应。

最终预测结果 $ \hat{Y} $ 是各个分解分量预测的加和：

\[\hat{Y} = \hat{Y}_T + \hat{Y}_S + \hat{Y}_R \]

4. 归一化步骤

在得到最终预测结果后，模型使用归一化步骤来确保输出和输入数据的统计特性一致：

\[\hat{Y}_t^i = \sqrt{\text{Var} [x_t^i] + \epsilon} \cdot \left( \frac{\hat{Y}_t^i - \beta}{\gamma} \right) + E_t [x_t^i] \]

其中，$ E_t[x_t^i]$ 和 $\text{Var}[x_t^i] $ 表示输入数据的期望和方差，用于将预测值拉回到原始数据的尺度。

SimTS: Rethinking Contrastive Representation Learning for Time Series Forecasting

框架

以下是基于SimTS模型的主要模块和公式的整理：

1. SimTS模型结构概述

SimTS是一种简单的时间序列预测模型，旨在通过自监督学习框架提高时间序列数据的表示学习效果。它通过对比损失函数学习时间序列的历史片段和未来片段之间的关系，从而生成有效的时间序列特征表示。

2. 模型输入与目标

给定一个时间序列数据 $ X = [x_1, x_2, \dots, x_T] \in \mathbb{R}^{C \times T} $，其中 $ C $ 表示特征数量，$ T $ 表示序列长度。模型的目标是通过历史片段 $ X^h = [x_1, x_2, \dots, x_K] ) 的表示来预测未来片段 ( X^f = [x_{K+1}, x_{K+2}, \dots, x_T] $ 的表示。

3. 主要模块

Siamese Network: 使用Siamese双网络结构来编码历史片段和未来片段。双网络共享权重，分别将 $ X^h $ 和 $ X^f $ 输入其中，以获得相应的潜在表示 $ Z^h $ 和 $ Z^f $。
Multi-Scale Encoder:
- 使用卷积层对时间序列数据进行多尺度编码。
- 通过投影层和多尺度的1D卷积层（不同大小的卷积核）提取局部和全局时间模式。
Predictor Network $ G_\phi $:
- 使用MLP网络预测历史片段的表示的最后一列，以生成未来的预测表示。
- 预测结果 $ \hat{Z}^f $ 和未来片段的编码表示 $ Z^f $ 之间的相似度被用作模型的优化目标。
Cosine Similarity Loss:
- 使用余弦相似性损失来最大化 $ \hat{Z}^f $ 和 $ Z^f $ 之间的相似度。

4. 公式推导

编码表示：编码器 ( F_\theta ) 将历史片段 ( X^h ) 和未来片段 ( X^f ) 映射到潜在表示空间中：

\[Z^h = F_\theta(X^h) = \{z_1^h, z_2^h, \dots, z_K^h\} \in \mathbb{R}^{C' \times K} \]
\[Z^f = F_\theta(X^f) = \{z_{K+1}^f, z_{K+2}^f, \dots, z_T^f\} \in \mathbb{R}^{C' \times (T - K)} \]
未来表示预测：使用MLP预测网络 ( G_\phi ) 以 ( Z^h ) 的最后一列 ( z_K^h ) 为输入，预测未来表示：

\[\hat{Z}^f = G_\phi(z_K^h) = \{\hat{z}_{K+1}^f, \hat{z}_{K+2}^f, \dots, \hat{z}_T^f\} \in \mathbb{R}^{C' \times (T - K)} \]
相似性损失：将预测的未来表示 ( \hat{Z}^f ) 和编码的未来表示 ( Z^f ) 作为正样本对，使用余弦相似度来衡量它们的相似性，计算公式为：

\[Sim(\hat{Z}^f, Z^f) = -\frac{1}{T - K} \sum_{i=K+1}^T \frac{\hat{z}_i^f \cdot z_i^f}{\| \hat{z}_i^f \|_2 \| z_i^f \|_2} \]
总损失：通过余弦相似性损失来优化历史表示和未来表示之间的关系，对于一个mini-batch ( D = {(X_i^h, X_i^f)}_{i=1}N ) 的损失为：

\[\mathcal{L}_{\theta, \phi}(D) = \frac{1}{N} \sum_{i=1}^N Sim(\hat{Z}_i^f, Z_i^f) \]
停止梯度操作：为了防止梯度反向传播到未来编码路径，SimTS在计算相似性损失时对 ( Z^f ) 施加了停止梯度操作 ( sg(\cdot) )：

\[\mathcal{L}_{\theta, \phi}(X^h, X^f) = Sim(\hat{Z}^f, sg(Z^f)) \]

5. 训练过程

训练过程主要包括以下步骤：

将时间序列分割为历史片段和未来片段。
使用多尺度编码器对历史片段和未来片段进行编码。
使用预测网络 $G_\phi $ 根据历史片段的编码表示预测未来片段的表示。
使用余弦相似性损失优化预测表示 $ \hat{Z}^f $ 和编码表示 $ Z^f $ 之间的相似性。

对比学习的计算

确实，在SimTS的对比学习框架下，真实的未来表示 $ Z^f $ 是未知的，模型的目标是通过历史片段来预测它。让我们再清晰地梳理一下SimTS如何进行对比学习：

1. 模型输入划分

将时间序列划分为：

历史片段 $ X^h = [x_1, x_2, x_3] $
未来片段 $ X^f = [x_4, x_5, x_6] $

2. 历史片段编码

使用编码器 $ F_\theta $ 将历史片段 $ X^h $ 映射到潜在空间，得到历史片段的表示：

\[Z^h = F_\theta(X^h) = [z_1^h, z_2^h, z_3^h] \]

3. 预测未来表示

使用预测网络 $ G_\phi $，以历史片段编码的最后一个时间步 $z_3^h $ 为输入，生成对未来片段的预测表示：

\[\hat{Z}^f = G_\phi(z_3^h) = [\hat{z}_4^f, \hat{z}_5^f, \hat{z}_6^f] \]

注意：这里的 ( \hat{Z}^f ) 是模型从历史信息中预测出的表示，是对未来时间步的估计。

4. 对比学习的目标

虽然真实未来表示 $Z^f = [z_4^f, z_5^f, z_6^f] $ 是未知的，但我们仍然使用它作为训练中的一个目标。SimTS设计了一个方式，通过对比预测的未来表示 $ \hat{Z}^f $ 和真实未来编码$( Z^f $，使得模型尽可能靠近真实未来的潜在表示。即：

构造正样本对：将 $ \hat{Z}^f$ 和 $ Z^f $ 视为一个正样本对。
相似性损失：计算预测的未来表示和真实未来表示之间的余弦相似性：

\[Sim(\hat{Z}^f, Z^f) = -\frac{1}{T - K} \sum_{i=K+1}^T \frac{\hat{z}_i^f \cdot z_i^f}{\| \hat{z}_i^f \|_2 \| z_i^f \|_2} \]
这里，负号表示将相似性转化为损失，以最大化相似性。

5. 停止梯度操作

由于我们希望模型主要从历史片段中学习对未来的预测，而不直接调整未来片段的编码，因此在 $ Z^f $ 上应用停止梯度操作 $ sg(\cdot) $，这样就不会反向传播到未来片段的编码路径。

总结

在SimTS中，真实的未来表示 $ Z^f $ 的确未知。通过对比学习框架，模型会从历史片段生成预测的未来表示 $ \hat{Z}^f $，并希望它与未来编码（即目标） $ Z^f $ 尽可能接近，从而逐步优化对未来的预测能力。

SimMTM: A Simple Pre-Training Framework for Masked Time-Series Modeling

框架

这里是关于 SimMTM（一种时间序列重构方法）的模块和公式整理。我们将按照模块顺序逐步说明。

1. 模型框架

SimMTM 的重构过程包含以下四个模块：

Masking（掩码处理）
Representation Learning（表示学习）
Series-wise Similarity Learning（序列级别相似性学习）
Point-wise Reconstruction（点级重构）

2. 公式详解

掩码处理

对于一批次的时间序列样本 ${ \{ \mathbf{x}_i \}_{i=1}^N }$，每个样本 ${ \mathbf{x}_i \in \mathbb{R}^{L \times C} }$ 包含 $L$ 个时间点和 $C$ 个观测变量。我们对每个样本随机掩盖部分时间点，公式如下：

\[\{ \bar{\mathbf{x}}_i^j \}_{j=1}^M = \text{Mask}_r(\mathbf{x}_i), \]

其中 $r \in [0,1]$ 表示掩码比例，$M$ 是超参数，定义了掩码序列的数量。${ \bar{\mathbf{x}}_i^j \in \mathbb{R}^{L \times C} }$ 表示掩盖后的第 $j$ 个时间序列样本，其中一部分时间点被置为零。

所有生成的掩码序列和原序列构成输入集：

\[\mathcal{X} = \bigcup_{i=1}^N \left( \{ \mathbf{x}_i \} \cup \{ \bar{\mathbf{x}}_i^j \}_{j=1}^M \right). \]

表示学习

通过编码器和投影层，我们可以获得点级别表示 $\mathbf{Z}$ 和序列级别表示 $\mathbf{S}$，定义如下：

\[\mathbf{Z} = \bigcup_{i=1}^N \left( \{ \mathbf{z}_i \} \cup \{ \bar{\mathbf{z}}_i^j \}_{j=1}^M \right) = \text{Encoder}(\mathcal{X}), \]

\[\mathbf{S} = \bigcup_{i=1}^N \left( \{ \mathbf{s}_i \} \cup \{ \bar{\mathbf{s}}_i^j \}_{j=1}^M \right) = \text{Projector}(\mathbf{Z}), \]

其中，$\mathbf{z}_i, \bar{\mathbf{z}}_i^j \in \mathbb{R}^{L \times d_{\text{model}}}$ 和 $\mathbf{s}_i, \bar{\mathbf{s}}_i^j \in \mathbb{R}^{1 \times d_{\text{model}}}$。

序列级别相似性学习

为了避免直接平均导致的过度平滑问题，我们利用序列级别表示 $\mathbf{S}$ 之间的相似性来进行加权聚合。相似性矩阵 $\mathbf{R}$ 计算如下：

\[\mathbf{R} = \text{Sim}(\mathbf{S}) \in \mathbb{R}^{D \times D}, \quad D = N(M + 1), \]

\[\mathbf{R}_{\mathbf{u}, \mathbf{v}} = \frac{\mathbf{u} \mathbf{v}^\top}{\|\mathbf{u}\| \|\mathbf{v}\|}, \quad \mathbf{u}, \mathbf{v} \in \mathbf{S}, \]

其中，$\mathbf{R}$ 是序列级别表示之间的成对相似性矩阵，用余弦距离计算。

点级聚合

基于学到的序列级别相似性，原始时间序列的第 $i$ 个点级重构表示 $\hat{\mathbf{z}}_i$ 定义为：

\[\hat{\mathbf{z}}_i = \sum_{\mathbf{s}' \in \mathbf{S} \backslash \{\mathbf{s}_i\}} \frac{\exp(\mathbf{R}_{\mathbf{s}_i, \mathbf{s}'}/\tau)}{\sum_{\mathbf{s}'' \in \mathbf{S} \backslash \{\mathbf{s}_i\}} \exp(\mathbf{R}_{\mathbf{s}_i, \mathbf{s}''}/\tau)} \mathbf{z}', \]

其中 $\mathbf{z}'$ 表示对应的点级表示，$\tau$ 是温度超参数。

3. 自监督预训练

SimMTM 的自监督学习通过重构损失监督，公式如下：

\[\mathcal{L}_{\text{reconstruction}} = \sum_{i=1}^N \|\mathbf{x}_i - \hat{\mathbf{x}}_i\|_2^2. \]

为了避免直接重构导致的平凡聚合，我们引入邻域假设，将时间序列流形结构校准到序列级别表示空间 $\mathbf{S}$。定义正负样本对：

正样本对：

\[(\mathbf{s}_i, \mathbf{s}_i^+), \quad \mathbf{s}_i^+ \in \{\bar{\mathbf{s}}_i^j\}_{j=1}^M. \]

负样本对：

\[(\mathbf{s}_i, \mathbf{s}_i^-), \quad \mathbf{s}_i^- \in \{\mathbf{s}_k\} \cup \{\bar{\mathbf{s}}_k^j\}_{j=1}^M, \; i \neq k. \]

约束损失

使用约束损失来优化学习到的序列级别表示：

\[\mathcal{L}_{\text{constraint}} = - \sum_{\mathbf{s} \in \mathbf{S}} \left( \sum_{\mathbf{s}' \in \mathbf{S}^+} \log \frac{\exp(\mathbf{R}_{\mathbf{s}, \mathbf{s}'}/\tau)}{\sum_{\mathbf{s}'' \in \mathbf{S} \backslash \{\mathbf{s}\}} \exp(\mathbf{R}_{\mathbf{s}, \mathbf{s}''}/\tau)} \right). \]

4. 总体优化目标

SimMTM 的总体优化目标定义为：

\[\min_{\Theta} \mathcal{L}_{\text{reconstruction}} + \lambda \mathcal{L}_{\text{constraint}}, \]

其中，$\Theta$ 表示模型的所有参数，$\lambda$ 是平衡重构损失和约束损失的超参数。

点集聚合

你观察得很准确！这一点级别的聚合公式确实类似于注意力机制，尤其是和加权平均的注意力机制相似。我们可以详细解析一下这个公式，看看它是如何通过类似注意力的方式来实现聚合的。

公式解读

公式定义如下：

\[\hat{\mathbf{z}}_i = \sum_{\mathbf{s}' \in \mathbf{S} \setminus \{\mathbf{s}_i\}} \frac{\exp(\mathbf{R}_{\mathbf{s}_i, \mathbf{s}'}/\tau)}{\sum_{\mathbf{s}'' \in \mathbf{S} \setminus \{\mathbf{s}_i\}} \exp(\mathbf{R}_{\mathbf{s}_i, \mathbf{s}''}/\tau)} \mathbf{z}', \]

其中：

$\hat{\mathbf{z}}_i$ 是第 $i$ 个时间序列点的重构表示。
$\mathbf{R}_{\mathbf{s}_i, \mathbf{s}'}$ 表示序列级表示之间的相似性，通过余弦相似度或其他相似性度量计算得到。
$\tau$ 是温度超参数，用于调整相似性分数的“锐化”或“平滑”程度。
$\mathbf{z}'$ 是对应的点级表示。

类似注意力机制的工作原理

相似性度量：$\mathbf{R}_{\mathbf{s}_i, \mathbf{s}'}$ 类似于注意力中的“点积”相似性。在注意力机制中，我们通常计算 query 和 key 的相似性，这里是通过计算当前点 $i$ 的序列表示 $\mathbf{s}_i$ 和其他序列 $\mathbf{s}'$ 的相似性来实现的。
Softmax 归一化：公式中的 $\exp(\mathbf{R}_{\mathbf{s}_i, \mathbf{s}'}/\tau)$ 被归一化为概率分布，这与注意力机制的 Softmax 过程类似，使得更相似的项得到更高的权重。
加权求和：最终的加权和会生成聚合后的 $\hat{\mathbf{z}}_i$，这是基于与 $\mathbf{s}_i$ 相似的其他序列的表示。这和注意力机制中的“值”的加权求和相似，这里则是利用其他点级表示 $\mathbf{z}'$ 的加权和来重构出 $\hat{\mathbf{z}}_i$。

直观理解

这种机制的目标是通过一组相关序列的表示来重构原始序列的点级表示。通过“注意力”机制，它能够关注到与当前序列最相似的其他序列，从而获得更加平滑和一致的表示。这种结构在重构任务中尤其有效，因为它可以有效地捕捉到时间序列数据中的相似模式，避免了直接平均可能导致的过度平滑问题。

总结

因此，这一结构可以被视为一种“注意力机制”的应用，通过加权不同序列的相似性来生成一个聚合的时间序列表示。

AutoTimes: Autoregressive Time Series Forecasters via Large Language Models

框架

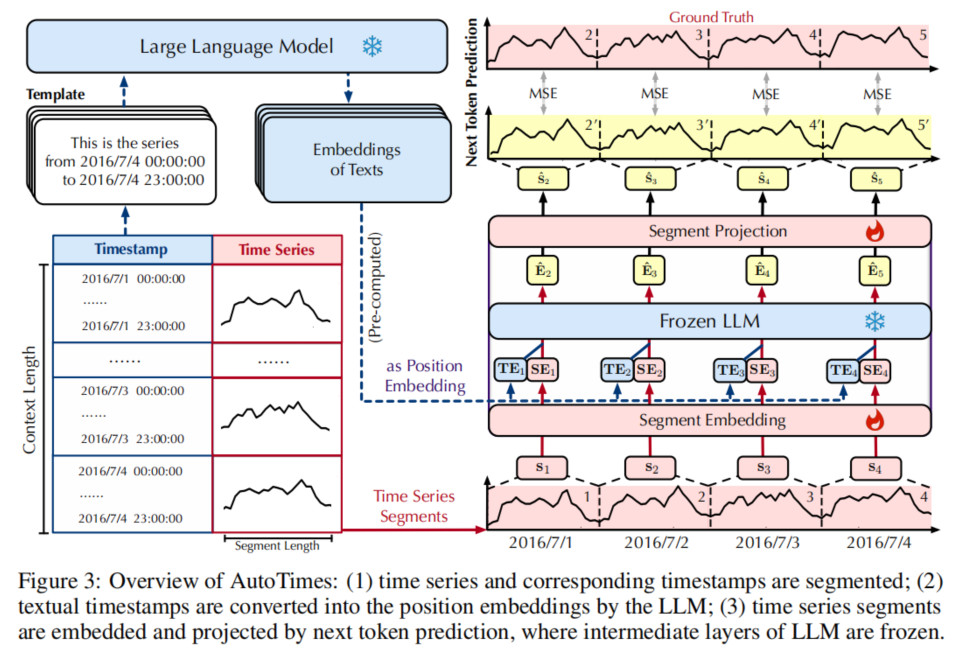
以下是关于 AutoTimes 框架的整体方法和公式的整理，使用和之前一致的 Markdown 格式和符号。

方法概述

AutoTimes 框架通过调整大语言模型（LLMs）来实现多元时间序列的预测。它利用 LLM 的自回归特性，将时间序列的特征作为输入进行预测，适配了适当的时间序列嵌入和对齐机制来预测未来的序列状态。

主要组成部分

1. 时间序列输入与预测目标

给定一个多变量时间序列的输入（回溯观察序列）：

\[\mathbf{x}_{1:L} = \{ \mathbf{x}_1, \ldots, \mathbf{x}_L \} \in \mathbb{R}^{L \times C} \]

其中，( L ) 表示时间步的长度，( C ) 表示变量的数量。

目标是预测未来 ( F ) 个时间步：

\[\mathbf{x}_{L+1:L+F} = \{ \mathbf{x}_{L+1}, \ldots, \mathbf{x}_{L+F} \} \in \mathbb{R}^{F \times C} \]

因此，我们的预测函数 ( f ) 被训练成从过去的观测序列和相应的时间戳映射到未来的预测：

\[f: (\mathbf{x}_{1:L}, \mathbf{a}_{1:L+F}) \mapsto \hat{\mathbf{x}}_{L+1:L+F} \]

3.1 模态对齐

时间序列 Token：
为了利用 LLM 的自回归预测能力，我们将时间序列数据分段为不重叠的时间片段，使其与 LLM 需要的 Token 输入格式对齐。这样可以有效减少自回归的长度，每个变量独立处理：

\[s_i = \{ x_{(i-1)S+1}, \ldots, x_{iS} \} \in \mathbb{R}^S, \quad i = 1, \ldots, N \]
接着，将每个片段 ( s_i ) 嵌入到 LLM 的隐空间：

\[\text{SE}_i = \text{SegmentEmbedding}(s_i), \quad i = 1, \ldots, N \]
位置嵌入：
时间戳作为位置嵌入，确保时间片段的时间顺序不被破坏。LLM 使用预计算的模板生成位置嵌入：

\[\text{TE}_i = \text{SelectLast} \left( \text{LLM}\left( \text{TimestampTemplate}(s_i) \right) \right) \]
最终，每个片段的 Token 嵌入 ( E_i ) 由片段嵌入和位置嵌入组合而成：

\[E_i = \text{SE}_i + \text{TE}_i \]

3.2 下一个 Token 预测

为了实现预测功能，将每个片段的嵌入通过 LLM 进行逐步处理，以生成下一个时间步的预测。给定长度为 ( NS ) 的输入序列，嵌入 ({E_1, \ldots, E_N}) 被逐步输入到 LLM 层中，生成每个时间片段的预测：

\[\{\hat{E}_2, \ldots, \hat{E}_{N+1}\} = \text{LLMLayers}(\{E_1, \ldots, E_N\}) \]

然后，每个预测的嵌入 (\hat{E}_i) 被映射回片段空间：

\[\hat{s}_i = \text{SegmentProjection}(\hat{E}_i), \quad i = 2, \ldots, N+1 \]

训练时，通过均方误差损失函数进行优化：

\[\mathcal{L}_{\text{MSE}} = \frac{1}{NS} \sum_{i=2}^{N} \| s_i - \hat{s}_i \|_2^2 \]

3.3 上下文内预测（In-Context Forecasting）

AutoTimes 利用 LLM 的上下文学习能力，通过扩展上下文（extended context）来进行多步预测，而无需对模型进行额外微调。通过历史的回溯预测对构建上下文，使得 LLM 能够适应新的预测需求。扩展上下文 ( C ) 包含早期的历史时间序列数据：

\[C = \{ \text{tsp}^{(j)} = \mathbf{x}_{\leq t_j} \text{ | earlier historical time series} \}, \quad j = 1, \ldots, m, \, t_j \leq L \]

最终的上下文内预测函数定义为：

\[f : (C, \mathbf{x}_{1:L}, \mathbf{a}_{1:L+F}) \mapsto \hat{\mathbf{x}}_{L+1:L+F} \]

上下文信息

是的，图中展示的“文本信息”是指将时间戳转化为一种文本格式，作为上下文信息提供给大语言模型（LLM）。具体来说，AutoTimes框架利用文本描述时间戳（例如“2016/7/4 00:00:00”到“2016/7/4 23:00:00”）并通过LLM生成其嵌入表示，这样可以引入时间上的位置信息，帮助模型识别数据的时间依赖性。

这个过程分为几个步骤：

时间戳文本化：将时间戳转换为自然语言句子（如左侧模板“这是2016年7月4日00:00到23:00的序列”）。
嵌入生成：将这些文本句子输入到LLM中生成相应的嵌入表示。
位置嵌入应用：使用这些嵌入作为时间序列的“位置嵌入”（Position Embedding），将时间信息引入时间序列的编码中，确保模型在预测时能够利用时间的先后顺序。

最终，这种时间戳的文本信息（即位置嵌入）与时间序列的特征表示结合，以便在LLM中实现上下文对齐。

PT-Tuning: Bridging the Gap between Time Series Masked Reconstruction and Forecasting via Prompt Token Tuning

框架

加入prefix的fine-tuning

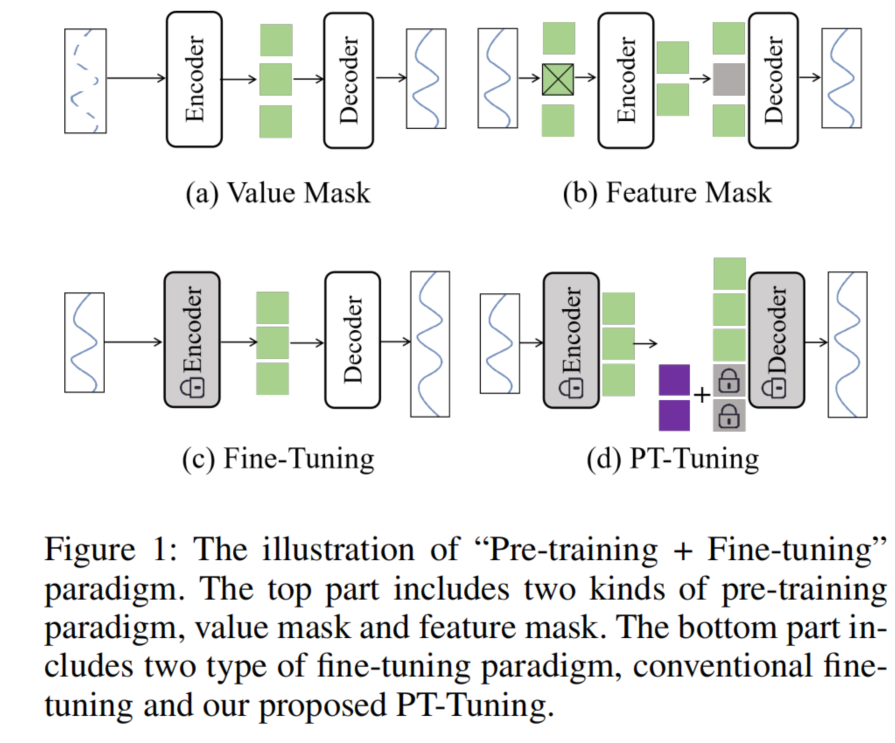
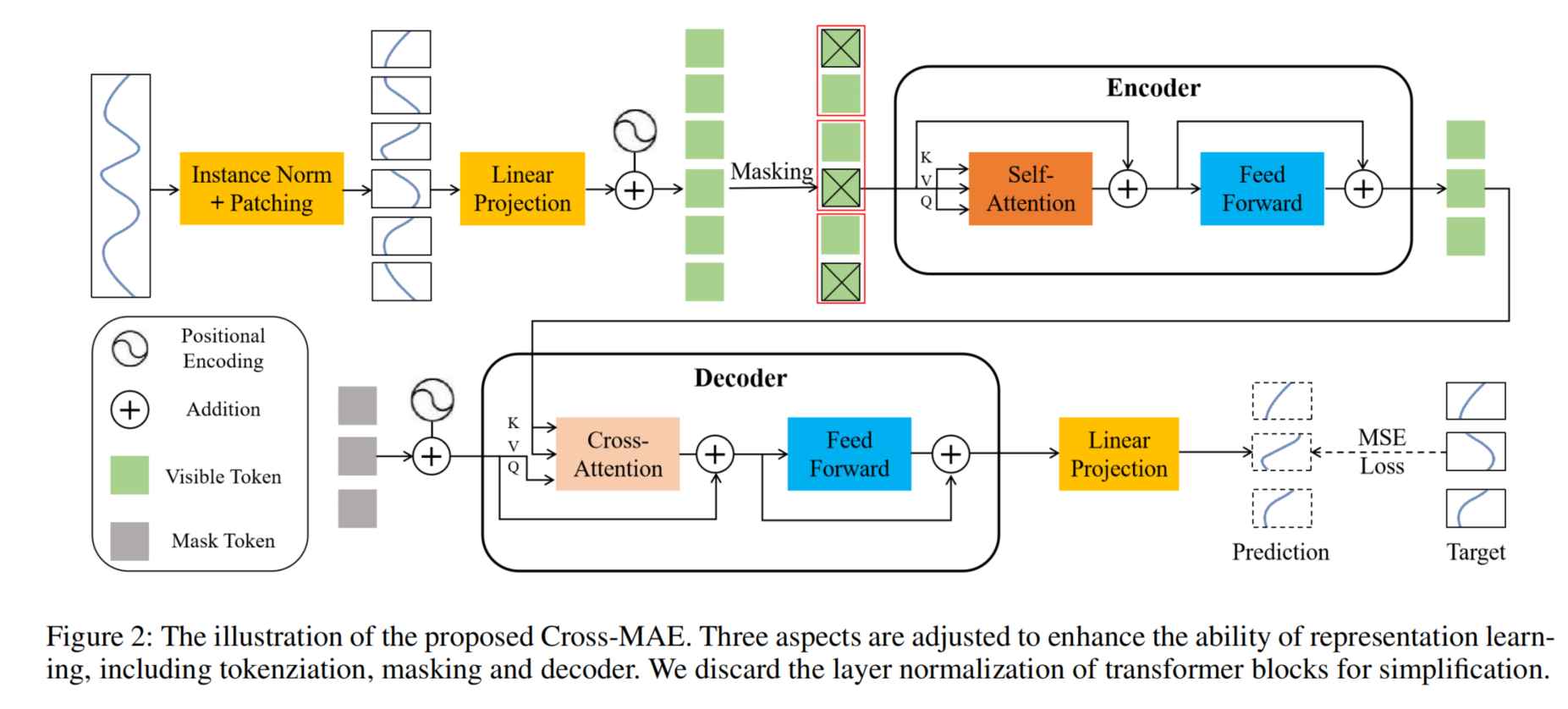
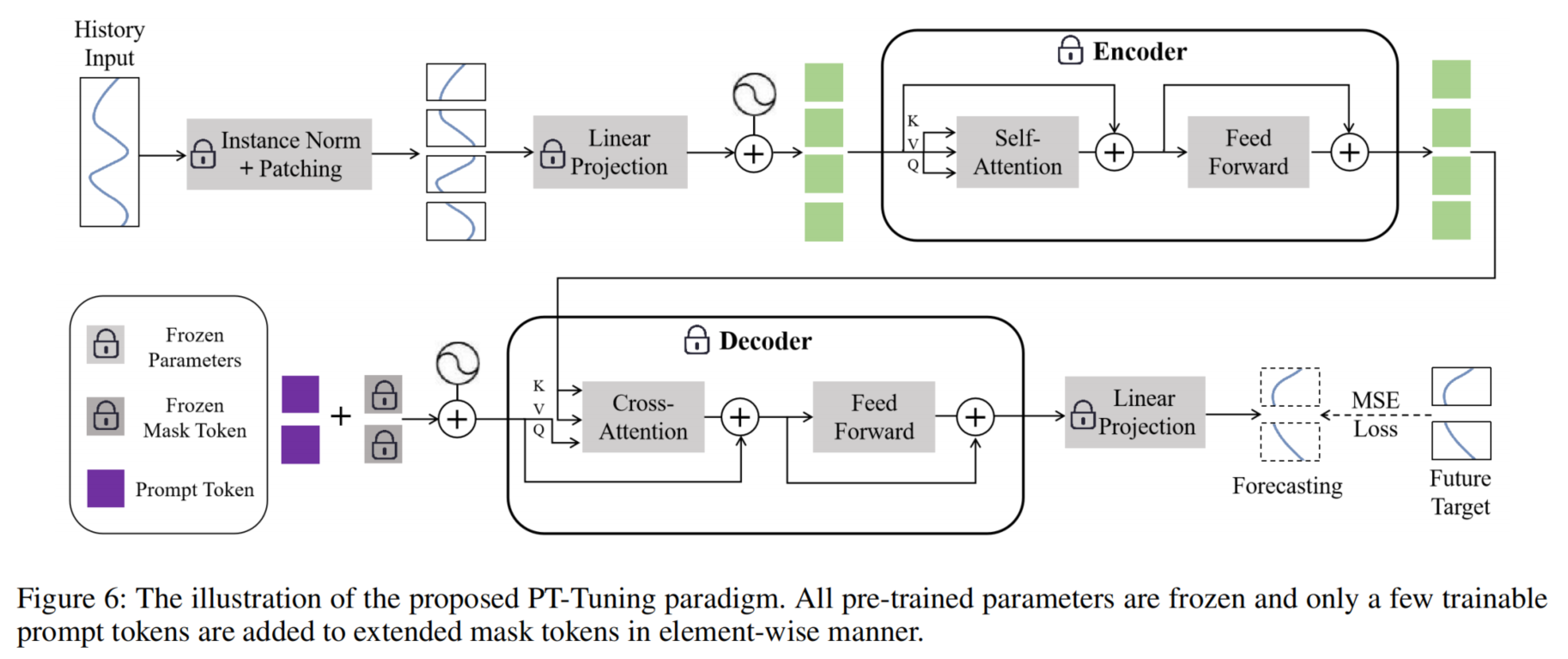
在这个 PT-Tuning（Prompt Token Tuning）结构中，主要利用 Transformer 的基础架构，通过引入 Prompt Token 作为一种前缀形式的标记来微调大规模预训练模型，使之适应时序数据的预测任务。以下是各个模块和公式的解读：

1. 模块解释

输入历史数据处理：
- 输入的历史数据首先通过 Instance Norm + Patching 进行标准化和切片，然后通过一个 线性投影（Linear Projection）将数据投影到潜在表示空间。这样处理后的历史数据可以进一步输入到 Encoder 进行特征提取。
Encoder 编码器：
- 在编码器中，经过标准化处理的数据通过自注意力机制（Self-Attention）和前馈神经网络（Feed Forward）模块提取特征。这些层中，模型参数是冻结的，不会被训练。这部分保持 Transformer 结构的特征提取能力，但不更新权重。
Prompt Token 引入：
- Prompt Token 作为额外的输入被添加到网络的输入中，用于为任务提供指导。它通过与 Mask Token 一同加入，帮助模型在微调过程中更好地适应目标任务的需求。
Decoder 解码器：
- 解码器部分通过交叉注意力（Cross-Attention）机制将历史数据和 Prompt Token 结合，通过前馈神经网络生成最终的预测值。这个结构类似于 Transformer 的解码器，但加上了 Prompt Token 以增强预测效果。
损失计算：
- 最后一步使用均方误差损失（MSE Loss）计算预测值与目标的差异，以优化微调的 Prompt Token。

2. 公式解读

公式 (1)：生成未来 Token

\[F = M + P + E_p \]
其中：
- ( M ) 表示 Mask Token，用作未来位置的占位符。
- ( P ) 表示 Prompt Token，提供任务指导信息。
- ( E_p ) 表示位置嵌入（Positional Embeddings），提供时间序列的位置信息。
- 通过该公式，可以生成用于未来位置的 token 表示。
公式 (2) 和 (3)：跨注意力机制
- 生成查询（Q）、键（K）和值（V）的表示：
  
  \[Q = L_q(F), \quad K = L_k(H), \quad V = L_v(H) \]
  其中 ( L_q, L_k, L_v ) 是多层感知器（MLP）层，将生成的未来 token 投影到 query 空间，并将历史数据的表示 ( H ) 投影到 key 和 value 空间。
- 交叉注意力的计算：
  
  \[\text{Attn}(Q, K, V) = \text{Softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V \]
  通过 Softmax 加权后的注意力得分，跨注意力机制结合了未来 token 和历史 token 的信息。这帮助模型在预测时能够有效利用历史信息。

PT-Tuning 的优势

PT-Tuning 可以在冻结模型参数的情况下，通过训练少量 Prompt Token 来实现任务的适应性。这减少了微调过程中的过拟合风险。
相较于传统的微调方法，它只需要对 Prompt Token 进行梯度更新，从而在保持记忆效率的同时实现任务适应性。

HiMTM: Hierarchical Multi-Scale Masked Time Series Modeling with Self-Distillation for Long-Term Forecasting

框架

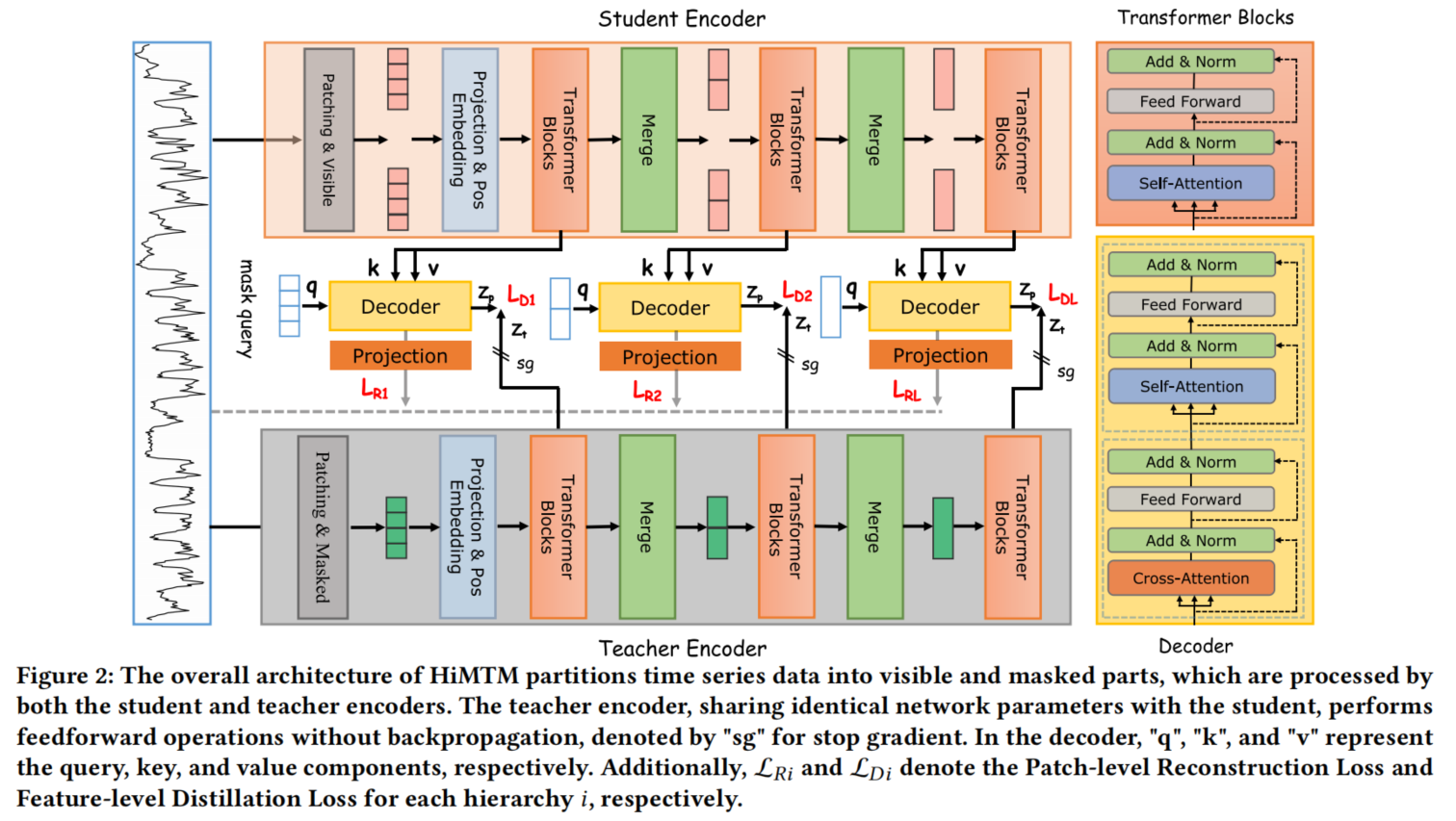
模块和公式整理

这部分内容描述了一种用于长期预测的分层自蒸馏掩码时间序列模型的框架，包括三个主要组件：学生编码器、教师编码器和解码器。这一方法引入了分层多尺度Transformer结构，通过分层补丁嵌入策略以及多层自蒸馏机制，提升了时间序列的特征表示学习能力。以下是各个模块和相关公式的详细解析：

3.1 总体架构

架构组成：包括学生编码器（Student Encoder）、教师编码器（Teacher Encoder）和解码器（Decoder）。
功能描述：
- 学生编码器：负责处理可见的时间片段，提取多尺度特征。
- 教师编码器：对掩码片段进行处理，生成多层次的特征指导信号。
- 解码器：使用交叉自注意力机制重构掩码片段。

3.2 分层多尺度Transformer（Hierarchical Multi-scale Transformer）

这一模块通过层次化的补丁分割策略提取多尺度特征，在每一层次的编码过程中合并相邻的更精细特征以生成更粗糙的补丁特征。

特征层次化生成：
- 每一层的特征生成公式：
  \[Z^{L+1} = \text{Hierarchy}^{L+1}(Z^L) \]
- 初始层特征的嵌入公式：
  \[Z^L = \begin{cases} \text{Patch\_Embed}(X), & \text{if } L = 1 \\ \text{Merge}(Z^{L-1}), & \text{if } L > 1 \end{cases} \]
其中 ( Z^L ) 表示第 ( L ) 层的特征表示。
多头自注意力机制（MSA）：
多头自注意力机制用于捕获远程依赖性，更新特征：

\[\text{MSA}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) \mathbf{W}^O \]
每个头的注意力计算为：

\[\text{head}_i = \text{Attention}(\mathbf{Q} \mathbf{W}_i^Q, \mathbf{K} \mathbf{W}_i^K, \mathbf{V} \mathbf{W}_i^V) \]
其中 ( \mathbf{W}_i^Q ), ( \mathbf{W}_i^K ), ( \mathbf{W}_i^V ) 为投影参数，Softmax函数用于归一化注意力得分。

3.3 模型预训练（Model Pre-training）

补丁和掩码处理：通过分层补丁划分策略实现对多尺度特征的处理，掩码操作在最粗粒度层执行。
- 初始嵌入公式：
  \[Z^0 = \text{Patch\_Embed}(X) + W_{\text{pos}} \]
其中 ( W_{\text{pos}} ) 为位置嵌入矩阵。
学生编码器：负责将可见的时间片段映射到潜在空间，生成多尺度特征表示。

\[Z_v = \text{Student\_Encoder}(X_v) \]
教师编码器：处理掩码片段，生成多层次特征并提供监督信号。

\[Z_m = \text{Teacher\_Encoder}(X_m) \]

3.4 模型优化目标

模型的优化包括两部分损失函数：

重构损失（Reconstruction Loss）：在每一层次上最小化掩码数据和重构数据之间的差异。
自蒸馏损失（Self-distillation Loss）：用于最小化学生编码器与教师编码器之间的特征差异，以提供多尺度层次上的监督。

优化目标函数为：

\[\mathcal{L} = \alpha \cdot \sum_{l=1}^L \mathcal{L}_D(Z_m^l, \hat{Z}_m^l) + \beta \cdot \sum_{l=1}^L \mathcal{L}_R(X_m^l, \hat{X}_m^l) \]

通过以上方法，该模型能够有效学习多尺度特征表达，同时通过自蒸馏机制进一步提升了对长时间序列的预测能力。

在该模型中，多尺度特征处理主要通过分层补丁划分策略（Hierarchical Patching Strategy）来实现，而多层次特征处理则通过教师编码器和学生编码器的层级结构来逐步提取更抽象的特征。以下是二者的具体实现方式：

1. 多尺度特征（Multi-scale Features）——通过补丁划分（Patching）

模型通过在不同时间尺度上生成补丁（patch）来实现多尺度特征的捕捉：

初始输入被划分成较小的补丁，这些补丁可能代表短时间间隔的特征。
随着层级的增加（层1到层L），模型将相邻的细粒度补丁合并为粗粒度的补丁，使得每个层级包含的信息具有不同的时间跨度。
最后在较高的层级，模型能够捕捉到更长时间范围内的特征，达到多尺度的目的。

通过这种分层补丁划分，模型能同时捕捉短期和长期的时间信息，从而实现对不同时间尺度上的特征建模。

2. 多层次特征（Multi-hierarchy Features）——通过教师和学生编码器的层级表示

多层次特征在模型的分层编码结构中体现，尤其是通过教师编码器和学生编码器的层级设计。在每一层，模型会生成并利用更抽象、更高级别的特征：

层级划分：教师编码器和学生编码器的层级结构负责在不同的层次上提取特征。最底层的编码器处理细粒度的补丁，随着层数的增加，逐步生成更加抽象的高层特征。
逐层合并与抽象：在每一层中，两个相邻的补丁通过合并操作生成更粗粒度的特征表示。模型通过这种逐层的合并与抽象，得到多个层次的表示，形成从细粒度到粗粒度的特征。
教师编码器的监督信号：教师编码器通过处理掩码片段，生成多层次的特征表示，并在每个层级上提供监督信号，指导学生编码器学习这些多层次的特征。通过这种方式，模型的学生编码器能够在各个层级上对不同层次的特征进行学习。

总结

多尺度：通过不同层级的补丁划分策略来获取短期和长期的时间信息，从而实现对不同时间尺度特征的捕捉。
多层次：通过学生编码器和教师编码器的层级结构实现，逐层提取从底层到高层的特征表示，每一层生成的特征都比前一层更加抽象和综合。教师编码器在各个层级上为学生编码器提供多层次的监督信号，以帮助模型学习到更全面的特征。

Generative Pretrained Hierarchical Transformer for Time Series Forecasting

框架

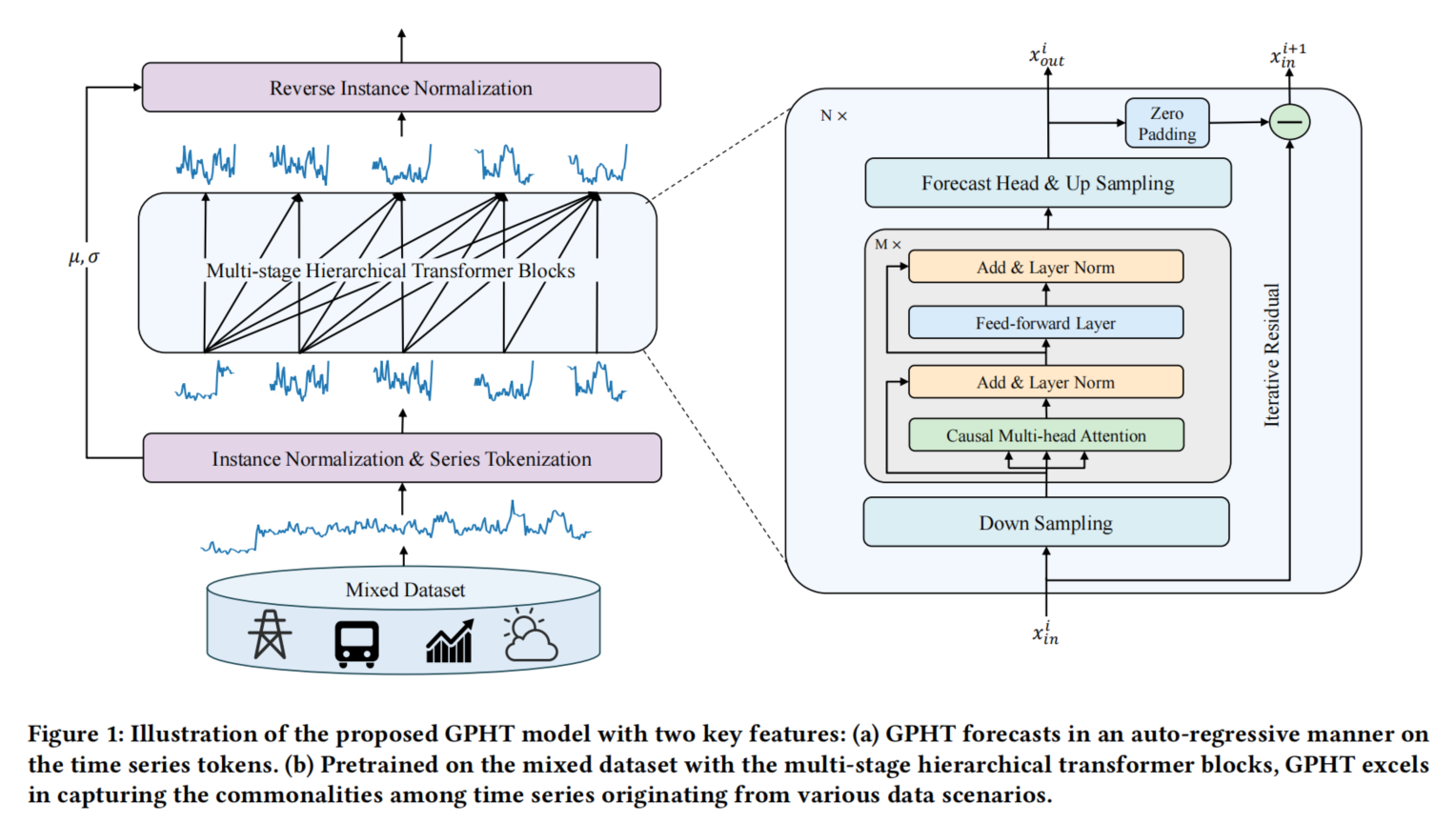
解读 GPHT 模型结构和公式

3.1 问题定义

给定一个输入时间序列 $ \mathcal{X} \in \mathbb{R}^{C \times L} $，模型的目标是精确预测未来的值 $\mathcal{Y} \in \mathbb{R}^{C \times H} $，其中 $ L $ 是回溯窗口长度，$ H $ 是预测的时间步长，$ C $ 是通道数。

Channel-Independent Assumption：假设每个通道（变量）是独立的，即模型会将多变量时间序列分解为多个独立的单变量时间序列进行预测，并将结果合并。
预训练数据集构造：将多种现实数据集的训练片段拼接成混合数据集，使 GPHT 适应多样化的时间模式。

3.2 系列标记化（Series Tokenization）

采用了 非重叠的标记化策略，将输入序列 $ \mathcal{X}$ 转化为一个时间序列标记集合 $ x \in \mathbb{R}^{C \times L' \times T} $。

$T $表示标记序列的长度，$ L' $是一个标记的长度，使得 $ T \times L' = L $。
归一化操作：使用实例归一化层，定义如下：

\[x_{\text{in}} = \frac{x - \mu}{\sigma + \epsilon} \]
其中，$ \mu $和 $ \sigma $ 分别是时间序列 $ \mathcal{X} $ 的均值和标准差。

3.3 分层 Transformer 块

引入了 多速率采样策略，通过逐层特征提取实现对多尺度模式的捕获。

下采样：对输入数据 ( x^i_{\text{in}} ) 进行下采样，应用不同的核大小 ( k_i ) 来进行特征提取。

\[h^i_{\text{in}} = \text{PE}(x^i_{\text{in}}) + \text{Emb}(x^i_{\text{in}}) \]
其中 $ \text{PE} $ 是位置嵌入层，$ \text{Emb} $ 是嵌入层。
输出预测：预测过程通过上采样操作实现：

\[ x^i_{\text{out}} = \text{UpSampling}(\text{Forecast}(h^i_{\text{out}})) \]

3.4 迭代残差学习

在每个阶段，输入序列的残差会被传递到下一阶段，用于逐步细化预测：

\[x^{i+1}_{\text{in}} = x^i_{\text{in}} - \text{PadFirstToken}(x^i_{\text{out}}) \]

3.5 优化目标

GPHT 的预测结果 $ y_{\text{pred}}$ 是所有分层 Transformer 块的输出和：

\[y_{\text{pred}} = \sum_{i=1}^{S} x^i_{\text{out}} \]
使用 均方误差（MSE） 作为损失函数：

\[ L = \text{MSE}(y_{\text{pred}}, \text{Concat}(X[:, T :], Y)) \]

3.6 推理

预训练任务与预测任务一致，因此 GPHT 可以直接应用于下游任务而无需额外微调。在推理阶段，每个输入时间步的预测值会顺序拼接，生成下一步的预测值。

与decoder-only类似

是的，这个框架确实很像 decoder-only 的结构。以下是一些具体的原因：

自回归结构：
- GPHT 在推理阶段采用的是自回归的预测方式，类似于自然语言处理中的生成模型。每一步的预测依赖于之前的输出，而非直接使用完整的输入序列，这种方式通常见于 decoder-only 模型。
无编码器（Encoder）部分：
- 这个框架没有传统 Transformer 中的编码器部分。通常，encoder-decoder 结构包含编码器对输入信息进行处理，然后通过解码器生成输出。而在 decoder-only 模型中，模型仅通过解码器逐步生成输出数据。GPHT 的结构也是通过多个阶段进行自回归预测，而没有专门的编码器。
自注意力机制与预测：
- GPHT 通过多层次的 Transformer 块实现逐步预测的功能，像 decoder-only 模型一样，使用自注意力机制逐步处理并生成新的时间步的预测。这意味着它在每一个步骤中，只基于之前生成的内容来预测后续的时间步长，而不会回头看完整的输入序列。
残差连接与迭代更新：
- 迭代残差学习的结构允许模型逐步更新预测结果，从粗略到精细逐层改善，这与 decoder-only 结构的自回归预测模式也非常相似。每一阶段的输出会作为下一阶段的输入，从而实现逐步精细化的预测。
位置嵌入与序列依赖：
- GPHT 使用位置嵌入（Position Embedding）和实例归一化（Instance Normalization）来引入时间信息，这些信息随着解码过程一起推进，符合 decoder-only 框架中的顺序依赖性设计。

因此，GPHT 确实可以被视作一种基于 decoder-only 的结构，使用自回归的方式逐步生成时间序列的未来值，通过多层次的解码块逐步提取并预测序列中的信息。

Self-supervised Trajectory Representation Learning with Temporal Regularities and Travel Semantics

数据

在这部分内容中，定义了相关的术语并明确了轨迹表示学习任务的问题背景。以下是整理的定义和问题描述：

定义

道路网络 (Road Network)
我们将道路网络表示为一个有向图 $ G = (\mathcal{V}, \mathcal{E}, F_{\mathcal{V}}, A) $，其中：
- $ \mathcal{V} = {v_1, \ldots, v_{|\mathcal{V}|}} $ 是顶点集合，每个顶点 $v_i $ 代表一个道路片段。
- $ \mathcal{E} \subseteq \mathcal{V} \times \mathcal{V} $ 是边集合，每条边 $ e_{i,j} = (v_i, v_j) $ 表示道路片段 $ v_i $ 和 $ v_j $ 之间的交叉点。
- $ N_i $ 表示道路片段 $ v_i $ 的邻居。
- $ F_{\mathcal{V}} \in \mathbb{R}^{|\mathcal{V}| \times d_{in}} $ 是道路片段的特征。
- $ A \in \mathbb{R}^{|\mathcal{V}| \times |\mathcal{V}|} $ 是一个二值邻接矩阵，表示网络 $ G $ 中的道路之间是否存在有向连接。
基于GPS的轨迹 (GPS-based Trajectory)
基于GPS的轨迹（或原始轨迹） $ T^{\text{raw}} $ 是一系列由GPS设备记录的空间-时间采样点序列，每个点 $ sp = \langle lat_i, lon_i, t_i \rangle $ 包含纬度、经度和时间戳信息。
道路网络约束的轨迹 (Road-network Constrained Trajectory)
道路网络约束的轨迹 $ T $ 是由用户生成的相邻道路片段的时间顺序序列，即 $ T = \langle (v_i, t_i) \rangle_{i=1}^m $，其中 $ v_i \in \mathcal{V} $ 表示第 $ i $个道路片段，$ t_i $ 是访问 $ v_i $ 的时间戳。

问题描述

给定轨迹数据集 $ \mathcal{D} = {T_i}_{i=1}^{|\mathcal{D}|} $ 和道路网络 $ G $，轨迹表示学习 (Trajectory Representation Learning, TRL) 的任务目标是学习每条轨迹 $ T_i \in \mathcal{D}$ 的一个通用的低维表示 $p_i \in \mathbb{R}^d $。具体来说，本文提出开发一个自监督框架，将每条轨迹编码为一个通用的 $ d $ 维表示向量 $ p_i $，该向量可以应用于各种下游任务，例如：旅行时间估计、轨迹分类和轨迹相似度计算。

在 Trajectory Pattern-Enhanced Graph Attention Layer (TPE-GAT) 中，$ p_{ij}^{\text{trans}} $ 表示 道路间的转移概率，用于反映两条道路之间的历史共现频率。

具体来说，$ p_{ij}^{\text{trans}} $ 的定义如下：

\[p_{ij}^{\text{trans}} = \frac{\text{count}(v_i \rightarrow v_j)}{\text{count}(v_i)} \]

其中：

$ \text{count}(v_i \rightarrow v_j) $表示在轨迹数据集中，从道路$ v_i $ 到道路 $v_j$ 的转移次数。
$ \text{count}(v_i) $ 表示轨迹数据集中道路 $ v_i $ 出现的总次数。

这个转移概率衡量了在轨迹中从道路 $ v_i $ 转移到 $ v_j $ 的可能性。通过加入转移概率 $p_{ij}^{\text{trans}}$，TPE-GAT 可以更好地捕捉道路之间的路径模式和频繁的交通模式，从而提升模型对轨迹的理解和表达能力。

时间间隔

在这里，$\Delta$ 是一个 时间间隔矩阵，用于表示不同道路节点之间的时间间隔。这个矩阵的构建方式是基于道路 $v_i$ 和 $v_j$ 在轨迹中的时间戳 $t_i$ 和 $t_j$，计算相对时间间隔 $\delta_{i,j}$：

\[\delta_{i,j} = |t_i - t_j| \]

通过这种方式，可以获得一个矩阵 $\Delta$，其每个元素$\delta_{i,j}$ 表示从 $v_i$ 到 $v_j$ 的时间间隔：

\[\Delta = \begin{bmatrix} \delta_{1,1} & \delta_{1,2} & \dots & \delta_{1,|T|} \\ \delta_{2,1} & \delta_{2,2} & \dots & \delta_{2,|T|} \\ \vdots & \vdots & \ddots & \vdots \\ \delta_{|T|,1} & \delta_{|T|,2} & \dots & \delta_{|T|,|T|} \end{bmatrix} \]

矩阵 $\Delta$ 的处理方式

缩放因子： 时间间隔 $\delta_{i,j}$ 越小，表明 $v_i$ 和 $v_j$ 之间的距离越近（即影响越大）；反之，时间间隔越大，影响越小。
衰减函数： 为了更合理地量化时间间隔的影响，引入了一个衰减函数来处理 (\Delta) 中的原始值：

\[\delta'_{i,j} = \frac{1}{\log(e + \delta_{i,j})} \]
其中，$e \approx 2.718$。这样处理后的 $\delta'_{i,j}$ 会随着时间间隔的增加而减小。
双线性变换： 为了进一步处理 (\delta'_{i,j})，采用了双线性变换，定义为：

\[\tilde{\delta}_{i,j} = (\text{LeakyReLU}(\delta'_{i,j} \cdot \omega_1)) \cdot \omega_2^T \]
其中，$\omega_1$ 和 $\omega_2$ 是可学习的参数，$\text{LeakyReLU}$ 是激活函数，帮助模型更好地捕捉不规则时间间隔的信息。

应用

经过处理后，$\tilde{\delta}_{i,j}$ 可以替换到时间间隔自注意力模块中，用于强化 Transformer 编码器对时间间隔信息的敏感度，从而更好地反映交通路段间不规则的时间关系和潜在的交通模式。这有助于模型捕捉到更为复杂的空间-时间依赖性。

框架

是的，您理解得很正确！这个模型的输入数据确实是一个人的 行车轨迹，包含了该人在道路网络中行驶过的道路节点以及相应的时间戳信息。这些轨迹数据在进入模型之前，经过一系列预处理，主要包括以下步骤：

轨迹数据表示：首先，将原始行车轨迹中的道路节点映射为图结构中的节点，同时根据时间戳信息计算出各个节点之间的时间间隔。这些节点（道路片段）及其特征会构成图结构输入模型。
特征构建和增强：每个道路节点不仅带有道路的基本信息（如类型、长度、车道数量等），还会根据轨迹中的访问频次、时间信息等增强特征。此外，还计算了时间间隔矩阵 (\Delta)，来表示不同节点之间的时间关系。
传入模型：经过预处理的数据（节点特征、图结构和时间间隔矩阵等）会传入模型。模型主要由以下几个模块组成：
- TPE-GAT（Trajectory Pattern-Enhanced Graph Attention Network）：负责将道路网络编码为道路节点表示，基于图注意力机制并结合时间间隔特征，生成包含交通模式的节点表示。
- TAT-Enc（Time-Aware Trajectory Encoder Layer）：将轨迹中的时间信息引入模型，利用 Transformer 编码器对不规则时间间隔进行建模，从而捕捉道路间的时间依赖性。
任务设计：模型的学习任务分为几个自监督任务，以便模型能够学习通用的轨迹表示。这些任务包括：
- Span-Masked Trajectory Recovery（跨段掩码轨迹恢复）：通过掩码一部分轨迹并让模型预测掩码部分，来学习轨迹结构。
- Trajectory Contrastive Learning（轨迹对比学习）：通过对比学习来捕捉轨迹中道路节点的共现关系，以便模型能够识别相似的交通模式。

通过这样的流程，这个模型在训练中可以从一个人的行车轨迹数据中学到一般性的轨迹表示。训练完成后，模型可以直接用于各种下游任务，比如轨迹分类、相似性计算和行驶时间估计等。

轨迹数据表示：首先，将原始行车轨迹中的道路节点映射为图结构中的节点，同时根据时间戳信息计算出各个节点之间的时间间隔。这些节点（道路片段）及其特征会构成图结构输入模型。
特征构建和增强：每个道路节点不仅带有道路的基本信息（如类型、长度、车道数量等），还会根据轨迹中的访问频次、时间信息等增强特征。此外，还计算了时间间隔矩阵 (\Delta)，来表示不同节点之间的时间关系。
传入模型：经过预处理的数据（节点特征、图结构和时间间隔矩阵等）会传入模型。模型主要由以下几个模块组成：
- TPE-GAT（Trajectory Pattern-Enhanced Graph Attention Network）：负责将道路网络编码为道路节点表示，基于图注意力机制并结合时间间隔特征，生成包含交通模式的节点表示。
- TAT-Enc（Time-Aware Trajectory Encoder Layer）：将轨迹中的时间信息引入模型，利用 Transformer 编码器对不规则时间间隔进行建模，从而捕捉道路间的时间依赖性。
任务设计：模型的学习任务分为几个自监督任务，以便模型能够学习通用的轨迹表示。这些任务包括：
- Span-Masked Trajectory Recovery（跨段掩码轨迹恢复）：通过掩码一部分轨迹并让模型预测掩码部分，来学习轨迹结构。
- Trajectory Contrastive Learning（轨迹对比学习）：通过对比学习来捕捉轨迹中道路节点的共现关系，以便模型能够识别相似的交通模式。

好的，让我们来详细探讨 TAT-Enc 层 的机制和 轨迹对比学习 的过程。

1. TAT-Enc层（Time-Aware Trajectory Encoder Layer）

TAT-Enc 层的设计核心是将时间信息引入轨迹编码。传统的 Transformer 编码器在计算注意力时，主要依赖位置编码，而 TAT-Enc 层还引入了时间间隔信息，以便更好地表示不同时刻经过的路段之间的关系。

TAT-Enc层主要分为两个模块：

(1) 轨迹时间模式提取模块 (Trajectory Time Pattern Extraction Module)

这个模块通过时间嵌入来捕捉周期性交通模式。对于每个轨迹节点（即道路节点）$ v_i $，我们会根据访问时间戳 $t_i $ 来生成时间嵌入。
具体来说，模型会用两种时间嵌入：分钟级时间嵌入（表示一天内的分钟数，用于反映日常周期性）和 星期级时间嵌入（表示一周内的天数，用于反映每周的周期性）。
然后，将这两个时间嵌入和道路节点的表示（即 TPE-GAT 层生成的节点表示）相加，从而得到增强后的节点表示 $ x_i = r_i + t_{mi}(t_i) + t_{di}(t_i) + pe_i $，其中 $pe_i $ 表示位置编码。

(2) 时间间隔自注意力模块 (Time Interval-aware Self-attention Module)

在标准的多头自注意力中，注意力是通过节点表示的 query、key 和 value 计算的。
但在 TAT-Enc 层的自注意力机制中，引入了时间间隔矩阵 ( \Delta ) 来建模道路节点之间的不规则时间间隔。这一矩阵中，$\delta_{i,j} = |t_i - t_j| $表示节点 $ v_i $和 $v_j $ 之间的时间间隔。
改进的自注意力计算公式：
\[TAh(Q_h, K_h, V_h) = \text{softmax}\left(\frac{Q_h K_h^T}{\sqrt{d'}} + \tilde{\Delta} \right) V_h \]
其中，$ \tilde{\Delta} $ 是经过缩放和非线性变换后的时间间隔矩阵，使得较短时间间隔的节点对的注意力得分更高。
这种时间间隔敏感的自注意力机制使得模型能够更好地捕捉道路节点之间的动态关系，尤其是在不同节点之间时间间隔较大的情况下，赋予它们不同的注意力权重。

2. 轨迹对比学习 (Trajectory Contrastive Learning)

轨迹对比学习的目的是让模型能够在嵌入空间中学习到不同轨迹的相似性和差异性，捕捉道路之间的共现关系和交通模式。

轨迹对比学习的核心步骤：

数据增强：
- 首先，对轨迹数据进行不同的增强方式，例如随机删除一些节点或在时间戳上添加噪声，生成“正样本”轨迹。
- 对于原始轨迹和增强后的轨迹，模型应该学会将其嵌入到相似的表示空间中。
对比学习损失：
- 使用对比学习损失（通常是 InfoNCE 损失），模型会在正样本对之间最大化相似度，并在负样本对（不同轨迹）之间最小化相似度。
- 损失函数的形式如下：
  \[L_{\text{contrastive}} = -\log \frac{\exp(\text{sim}(p_i, p_i^+)/\tau)}{\sum_{j=1}^{N} \exp(\text{sim}(p_i, p_j)/\tau)} \]
  其中，$ p_i $ 是原始轨迹的表示，$ p_i^+ $ 是增强后的轨迹表示，$ p_j $ 是负样本轨迹表示，$ \text{sim}(\cdot) $ 表示相似度（例如余弦相似度），$ \tau $ 是温度系数。
- 这样，模型会通过对比学习来学习轨迹间的语义相似性，使得相似的轨迹在嵌入空间中更接近，而不相似的轨迹则更远。

总结

TAT-Enc 层通过时间模式提取和时间敏感自注意力机制来对轨迹数据进行编码，使得模型可以更好地捕捉轨迹中的时间特征。
轨迹对比学习则通过对比学习损失和数据增强，使模型学会将相似轨迹嵌入到相似的表示空间，增强了模型对不同交通模式和共现关系的理解。

这种设计使得模型在处理轨迹数据时，能够兼顾道路网络中的空间结构和时间特征，从而在多种轨迹分析任务中表现出更好的泛化能力。

A TIME SERIES IS WORTH 64 WORDS: LONG-TERM FORECASTING WITH TRANSFORMERS

框架

我会帮助整理这些模块和公式的结构与作用。首先，结合图示和文本内容，PatchTST模型的框架包含以下主要组成部分：

1. 模型结构

输入与目标：PatchTST旨在对多变量时间序列数据进行预测。假设输入序列具有长度 $L$ 的窗口 $(x_1, \ldots, x_L)$，目标是预测未来的 $T$ 个值 $(x_{L+1}, \ldots, x_{L+T})$。
通道独立性：时间序列的每个变量视为独立通道进行处理，并输入到Transformer编码器中。

2. 前向过程

输入分离与通道处理：多变量时间序列拆分为每个变量独立的一元序列，表示为 $\mathbf{x}_{1:L}^{(i)}$，每个一元序列作为输入送入Transformer编码器。
Patch分块：每个一元序列按照特定的块长度 $P$ 和步长 $S$ 分成不重叠的patch。Patch数量为 $N = \left\lfloor \frac{L - P}{S} \right\rfloor + 2$。
- Patch减少了输入token数量，降低了计算复杂度。

3. Transformer编码器

编码过程：每个patch经过投影矩阵 $W_p \in \mathbb{R}^{D \times N}$ 映射到Transformer隐空间。
多头自注意力：计算Attention得分并生成注意力矩阵，公式如下：

\[ O_h^{(i)T} = \text{Attention}(Q_h^{(i)}, K_h^{(i)}, V_h^{(i)}) = \text{Softmax}\left(\frac{Q_h^{(i)} K_h^{(i)T}}{\sqrt{d_k}}\right) V_h^{(i)} \]

最后得到注意力输出 $O_h^{(i)} \in \mathbb{R}^{D \times N}$。

4. 损失函数

均方误差损失：用MSE度量模型预测与真实值的差异。总体目标损失表示为：

\[ \mathcal{L} = \mathbb{E}_{\mathbf{x}} \frac{1}{M} \sum_{i=1}^{M} \|\hat{\mathbf{x}}_{L+1:L+T}^{(i)} - \mathbf{x}_{L+1:L+T}^{(i)}\|_2^2 \]

5. 自监督表示学习

自监督学习目标：通过对输入片段进行掩码和重构，来学习抽象特征表示。

同一时间序列不同patch的注意力

是的，PatchTST模型中的Transformer编码器确实是在同一条时间序列内，不同patch之间进行自注意力计算。这种设计方式的核心在于：

时间序列分块：每条一元时间序列会根据设定的patch长度 $P$ 和步长 $S$ 被划分为多个不重叠的patch，这些patch相当于时间上的一个个片段。
同序列内的依赖建模：在Transformer中，每个patch通过自注意力机制与其他patch交互。这种方式可以捕捉时间序列在不同片段之间的依赖关系，而不仅仅是每个时间点的独立关系。
自注意力作用范围：自注意力机制允许每个patch的表示受到序列中其他patch（在同一条序列内）的影响，能够建模长时间的依赖性和全局信息。
不依赖于多变量通道的交互：由于模型在每个一元序列上独立地执行Transformer编码器，因此不同通道间不会进行直接的信息交换，每个时间序列通道的依赖关系在各自的时间轴上被单独建模。

这种设计有助于减少计算复杂度，因为在每条一元序列中各patch之间进行注意力计算不需要处理多变量之间的交互。这也是PatchTST模型的一个特点，即在通道独立的设置下，只对每个时间序列内部的patch做自注意力计算。

One Fits All: Universal Time Series Analysis by Pretrained LM and Specially Designed Adaptors

在您提供的算法框架中，有多个适配器（adapters）模块，这些适配器用于增强不同方面的特征。这里的适配器模块包括：

1. Instance Normalization

公式 (1) 描述了实例归一化过程：
\[\hat{X} = \frac{X - Exp}{\sqrt{Var + \epsilon}} \]
它通过减去均值并除以标准差来对每个时间序列实例进行归一化，从而减少训练和测试数据间的分布偏移。

2. Temporal & Channel Adapter

这是一个瓶颈结构的适配器。首先将高维度的通道信息投影到低维，然后通过两层 MLP 后再还原到高维。
主要用于捕捉时间维度和通道之间的关联性，减少直接建模通道间关系的过拟合风险。

3. Frequency Adapter

频率适配器利用快速傅里叶变换（FFT）将时间序列数据转换到频率域。
公式 (2) 表示了这一过程的转换，公式如下：
\[\hat{X}_{\text{freq}} = \text{iFFT}(W_l \cdot \text{FFT}(X_{\text{patched}})) \]
通过嵌入模块获得的适配器提示（公式 (3)）用于帮助 Transformer 捕捉整体的时间序列特征。

4. Anomaly Adapter

该适配器用于异常检测，主要是为了捕获对比偏差（contrastive bias），即正常信号会周期性地重复，而异常信号不会。
公式 (5) 描述了基于 KL 散度的损失计算：
\[\text{loss}_{\text{discrepancy}}^l = \text{KL}(\hat{A}_l || A^{\text{anomaly}}_l) \]
公式 (6) 和 (7) 定义了自注意力矩阵 $\hat{A}_l$ 和异常适配器矩阵 $A^{\text{anomaly}}_l$ 的具体计算方式。

Temporal & Channel Adapter 我感觉这个Adapter就是一个降维的处理，类似于MLP

是的，您理解得很准确。Temporal & Channel Adapter 确实可以看作是一种降维处理方式，核心结构类似于多层感知机（MLP）的瓶颈结构。具体来说，这个适配器采用了以下的降维策略：

降维（Bottleneck）结构：首先将高维的通道信息压缩到一个较低的维度。这一步是通过一个线性层完成的，将原始的高维空间映射到一个低维空间。这种方式可以减少通道间冗余信息，从而更好地捕捉时间序列数据的特征。
非线性激活：在降维之后，适配器通常会应用一个激活函数（例如 ReLU 或者 LeakyReLU），帮助模型学习非线性特征。
还原维度：在低维空间中通过两层 MLP 处理后，再将数据映射回原始的高维空间。这一步的目标是保留降维过程中提取的核心特征，同时恢复输入的原始维度。
跨通道和时间维度的关联性：由于时间序列数据通常具有跨时间和跨通道的相关性，直接对每个通道建模可能导致过拟合风险。因此，这种瓶颈式结构不仅降低了计算复杂度，还允许模型在较低维度空间中学习跨通道的关联性，增强模型的泛化能力。

总结

这种 Temporal & Channel Adapter 设计与传统的 MLP 类似，但它是专门为时间序列数据中的通道相关性和时间依赖性而设计的。它通过降维和还原过程帮助模型在低维空间中学习重要特征，减少过拟合风险，同时保留数据中的关键信息。这种方式对于包含大量通道的多变量时间序列数据特别有效。

Anomaly Adapter中的对比是对同一时间序列进行对比，还是对不同时间序列进行对比

Anomaly Adapter 中的对比是针对同一时间序列的不同部分进行对比，而不是对不同时间序列进行对比。这种对比的核心思想是利用正常模式与异常模式的不同特征来检测异常。具体来说，该适配器通过以下方式实现对比：

对比偏差（Contrastive Bias）：正常的时间序列通常会呈现周期性或重复性模式，而异常信号则不会表现出这种规律。这种差异被称为对比偏差。通过对同一时间序列内部的不同部分进行对比，模型可以学习到正常模式下的规律性特征，而异常模式则会缺少这些特征。
自注意力矩阵中的对比：Anomaly Adapter 会在自注意力矩阵中捕捉这种对比偏差。具体来说，在时间序列的正常片段中，注意力矩阵会表现出清晰的周期性或重复性结构，而在异常片段中，这种结构会被打破。因此，通过对比自注意力矩阵中是否存在这种规律性，可以帮助识别异常信号。
Kullback-Leibler (KL) 散度：为了量化这种对比，Anomaly Adapter 将自注意力矩阵的分布与通过对比得到的“正常”模式进行 KL 散度计算。如果计算出的散度较大，说明当前序列片段与正常模式存在较大差异，从而可能是异常。

小结

因此，Anomaly Adapter 的对比是基于同一时间序列的不同部分进行的，而不是跨不同时间序列。它通过对比自注意力矩阵中的周期性和重复性特征来捕捉异常，而不是在不同时间序列间寻找异常。

正常模式是预定的么？而自注意力矩阵是计算的？

是的，您的理解是正确的。

1. 正常模式是否预定？

正常模式并不是“预定的”，而是通过模型在训练过程中自动学习得到的。模型在训练时会接触到大量的正常数据，因此能够学习到正常数据在自注意力矩阵中的典型模式（即周期性和重复性特征）。这些特征形成了模型对于“正常模式”的内部表示。在实际应用中，模型会将新的数据与这种正常模式进行对比，以判断是否存在异常。

2. 自注意力矩阵的计算

自注意力矩阵确实是通过计算得到的。它是通过 Transformer 自注意力机制生成的。在 Transformer 中，每个时间步的特征向量会被映射为查询（Query）、键（Key）和值（Value），然后计算这些查询与键之间的相似度（即注意力权重），从而形成自注意力矩阵。

具体流程

学习正常模式：在训练过程中，模型会通过大量正常数据生成的自注意力矩阵来捕捉正常情况下的模式，比如时间序列中的周期性或重复性。这些模式不是人为设定的，而是模型通过训练自动得到的隐含特征。
生成自注意力矩阵：对于每个输入的时间序列，模型会计算自注意力矩阵。该矩阵反映了序列中各时间点之间的相似度或依赖关系，周期性或规律性会在矩阵中表现出类似的模式。
对比与检测：在检测过程中，Anomaly Adapter 会将当前时间序列生成的自注意力矩阵与“正常模式”进行对比。如果当前矩阵中的模式显著偏离正常模式（即缺少规律性、周期性等特征），则认为该时间序列片段可能存在异常。

总结

正常模式是模型在训练时自动学习得到的周期性或重复性特征。
自注意力矩阵通过 Transformer 机制计算得到，反映了时间序列中各时间点之间的关联性。
Anomaly Adapter 通过比较自注意力矩阵与正常模式的差异来检测异常，从而捕捉时间序列中潜在的异常信号。

LLM4TS: Aligning Pre-Trained LLMs as Data-Efficient Time-Series Forecasters

框架

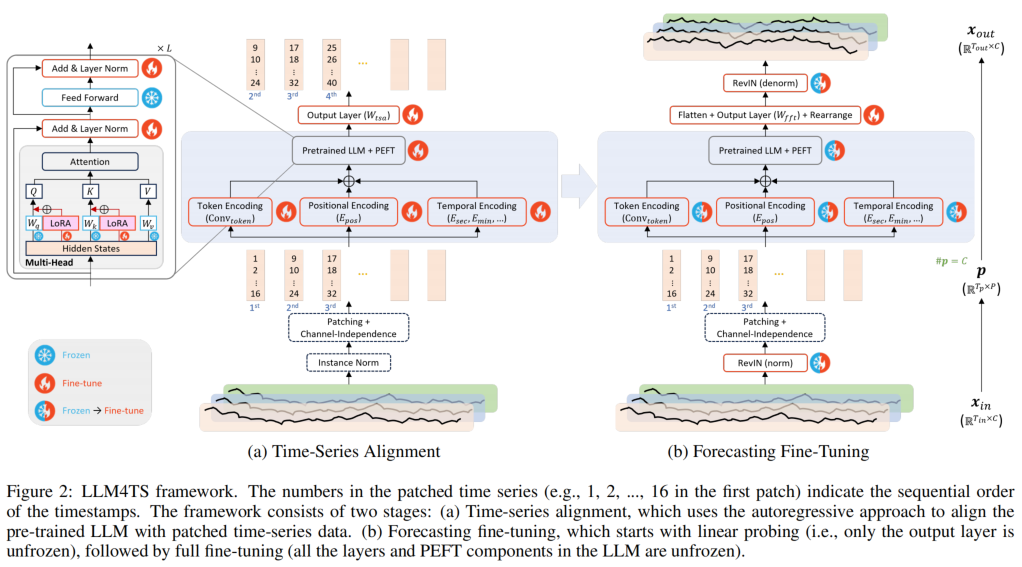
好的，以下是根据您提供的符号和语言规则整理的模型结构和公式概述：

1. 时间序列对齐阶段 (Time-Series Alignment Stage)

实例归一化 (Instance Normalization, IN)：对于每个输入时间序列样本 $ x_{\text{in}} \in \mathbb{R}^{T_{\text{in}} \times C} $，应用实例归一化以获得零均值和单位方差的标准化时间序列 $ x_{\text{normed}}$：

\[ x_{\text{normed}} = \text{IN}(x_{\text{in}}) \]

时间序列分块 (Time-Series Tokenization)：
- 通道独立性 (Channel Independence, CI)：将多变量时间序列的各通道独立处理，调整数据的维度。
- 补丁分块 (Patching)：将时间步长分组为补丁，以减少序列长度并转化为补丁令牌：
  \[p = \text{patching}(\text{CI}(x_{\text{normed}})) \]
时间序列编码层 (Encodings for Time-Series Data)：
- 令牌编码 (Token Encoding)：使用卷积操作（ConvToken）对补丁进行编码，生成令牌嵌入 $ e_{\text{token}} \in \mathbb{R}^{T_p \times D} $：
  \[e_{\text{token}} = \text{ConvToken}(p) \]
- 位置编码 (Positional Encoding)：为每个补丁添加位置嵌入 ( e_{\text{pos}} )：
\[ e_{\text{pos}} = E_{\text{pos}}(i) \]
- 时间编码 (Temporal Encoding)：聚合时间相关属性，形成时间嵌入 ( e_{\text{temp}} )：
  \[e_{\text{temp}} = \text{Pooling} \left( \sum_{a \in \{\text{sec, min, hour, ...}\}} E_a(t_a) \right) \]
综合嵌入 (Combined Embedding)：将令牌、位置和时间嵌入组合成最终的补丁嵌入 $ e $：

\[ e = e_{\text{token}} + e_{\text{pos}} + e_{\text{temp}} \]

预训练语言模型处理 (Pre-Trained LLM Processing)：将嵌入 ( e ) 输入预训练的Transformer层 (TBs)：

\[z = \text{TBs}(e) \]
预测层 (Prediction Layer)：使用线性层 $ W_{\text{tsa}} $ 将输出 $ z $转化为预测补丁 $ \hat{p}_{\text{shifted}} $：

\[ \hat{p}_{\text{shifted}} = z W_{\text{tsa}}^T \]

时间序列对齐损失函数 (Loss Function for Time-Series Alignment)：计算预测补丁 $ \hat{p}{\text{shifted}}$ 和真实补丁 $ p{\text{shifted}} $的均方误差 (MSE)：

\[ L_{\text{tsa}} = \text{MSE}(p_{\text{shifted}}, \hat{p}_{\text{shifted}}) \]

2. 预测微调阶段 (Forecasting Fine-Tuning Stage)

可逆实例归一化 (Reversible Instance Normalization, RevIN)：用于处理训练和测试数据间的分布漂移。
- 归一化步骤：
  \[p = \text{patching}(\text{CI}(\text{RevIN}_{\text{norm}}(x_{\text{in}}))) \]
- 反归一化步骤 (Denormalization)：在本阶段的未分块预测数据上应用。
输出层 (Output Layer for Forecasting)：
- 将最终嵌入$ z $展平并转化为未来数据的预测 $\hat{x}_{\text{out}}$：
\[ \hat{x}_{\text{out}} = \text{RevIN}_{\text{denorm}}(\text{Rearrange}(\text{Flatten}(z) W_{\text{fft}})) \]
预测微调损失函数 (Loss Function for Forecasting)：计算预测的未来数据$ \hat{x}{\text{out}} $ 与真实未来数据 $ x{\text{out}} $的均方误差 (MSE)：

\[ L_{\text{fft}} = \text{MSE}(x_{\text{out}}, \hat{x}_{\text{out}}) \]

此处描述的模块和公式涵盖了模型对齐和微调阶段的操作，利用实例归一化、通道独立性、补丁分块以及Transformer层来有效地预测时间序列结果。

这里token embedding和temporal embedding分别表示什么

您这样理解是正确的！具体来说：

令牌编码 用来处理交通数据的主要特征维度（即流量数据），它专注于从连续的时间步中提取局部的特征，生成一个固定的向量表示。因此，令牌编码主要对 流量信息 进行编码处理，捕捉流量数据随时间的变化模式。
时间编码 则是处理 时间特征（例如 day 和 week），将这些时间上下文信息编码进模型。时间编码提供了每个时间步的时间标识（例如，一天中的哪个小时、一周中的哪一天），从而帮助模型理解时间上的周期性和规律性，这对于交通数据的时序模式是非常关键的。

例子总结

假设您的交通数据每小时记录一次，数据格式为 [流量, day, week]：

令牌编码 会将每小时的流量数据进行处理，提取出流量的局部时序特征。
时间编码 则为每个时间步添加 day 和 week 信息，让模型能知道当前时间步是在星期几和一天中的哪个时间段，从而帮助模型识别流量的周期性模式。

结论

令牌编码负责流量数据的处理，生成每个时间片段的局部特征。
时间编码负责 day 和 week 时间特征 的处理，帮助模型理解时间上的上下文信息。

这样模型既能捕捉到流量随时间变化的模式，也能结合 day 和 week 的时间特征，实现对周期性模式的理解。您这样理解是非常准确的！

ForecastPFN: Synthetically-Trained Zero-Shot Forecasting

框架

以下是文章中关于ForecastPFN（基于先验数据拟合网络的零样本预测）的主要模块和公式的总结：

1. Prior-Data Fitted Networks（PFNs）背景

目标：通过训练网络学习在时间 $ t $ 上的先验数据分布，从而进行时间序列预测。
输入：一个时间序列 $ D = {(t, y_t)}_{t=1}^{T'} $ 和预测时间点 $T $。
后验预测分布（Posterior Predictive Distribution, PPD）：在给定时间 $ T $ 和数据 $ D $ 下，预测点 $ y $ 的分布为：
\[p(y \mid T, D) \propto \int_{\Phi} p(y \mid T, \varphi)p(D \mid \varphi)p(\varphi)d\varphi \]
训练方法：通过合成先验拟合（synthetic prior-fitting）来逼近该后验分布，采用交叉熵损失或均方误差损失进行优化。

2. 为时间序列定义合成先验（Defining a Synthetic Prior for Time Series）

合成数据生成：假设时间序列数据有两个独立的组成部分——底层趋势 ( \psi(t) ) 和噪声 ( z_t )。
公式表示：给定时间序列的值可以表示为：

\[y_t = \psi(t) \cdot z_t = \text{trend}(t) \cdot \text{seasonal}(t) \cdot z_t \]
- trend(t)：趋势项，结合线性和指数项。
- seasonal(t)：周期性项，结合了周、月和年的周期性特征。
- 噪声 $ z_t $：基于Weibull分布模拟。
每个周期成分（如周、月、年）的公式如下：

\[\text{seasonal}_\nu(t) = 1 + m_\nu \sum_{f=1}^{\lfloor p_\nu/2 \rfloor} \left( c_{f,\nu} \sin\left( \frac{2\pi f t}{p_\nu} \right) + d_{f,\nu} \cos\left( \frac{2\pi f t}{p_\nu} \right) \right) \]
- 其中 $p_\nu $ 表示不同的周期（例如，7天、30.5天、365.25天）。

3. ForecastPFN: 用于零样本预测的PFN设计

架构：使用一个基于Transformer的模型，包含一个多头注意力层和两个前馈层。
输入数据：以令牌（tokens）的形式输入模型，包含时间戳 $ t $、数值 $ y_t $ 以及查询时间 $ T $。
特点：模型支持任意未来日期的预测，不需要固定大小的输入，且不要求输入令牌是连续的。