luogu通道

ybt通道

1885：【14NOIP提高组】寻找道路


时间限制: 1000 ms         内存限制: 131072 KB
提交数: 180     通过数: 64

【题目描述】

在有向图G中，每条边的长度均为1，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2．在满足条件1的情况下使路径最短。

注意：图G中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

【输入】

第一行有两个用一个空格隔开的整数n和m，表示图有n个点和m条边。

接下来的m行每行2个整数x、y，之间用一个空格隔开，表示有一条边从点x指向点y。

最后一行有两个用一个空格隔开的整数s、t，表示起点为s，终点为t。

【输出】

输出只有一行，包含一个整数，表示满足题目描述的最短路径的长度。如果这样的路径不存在，输出-1。

【输入样例】

3 2
1 2
2 1
1 3

【输出样例】

-1

【提示】

【输入输出样例说明】

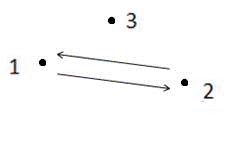
如上图所示，箭头表示有向道路，圆点表示城市。起点1与终点3不连通，所以满足题目描述的路径不存在，故输出-1。

【输入输出样例2】

输入：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出:

3

【输入输出样例说明】

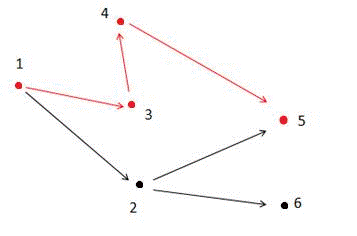
如上图所示，满足条件的路径为1->3->4->5。注意点2不能在答案路径中，因为点2连了一条边到点6，而点6不与终点 5 连通。

【数据说明】

对于30%的数据，0<n≤10，0<m≤ 20；

对于60%的数据，0 <n≤100，0<m≤2000；

对于100%的数据，0 <n≤10,000，0<m≤200,000，0< x，y，s，t≤n，x≠t。

 

*******************************************************************************************************************************************************

题解：题目有两个要求，其一：经过的点的出边要直接或间接到达终点，其二即为最小路

在第一个条件当中，要求我们这个出边不能到达无法经过终点的点

通过反向建图，从图2中，可以将    点6筛除；

通过6 找回它的出处即为2，将其标记；

最后正向建图，忽略掉标记的，然后暴力的正向SPFA下去，就AC了

上代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<queue>
#define mem(a,t) memset(a,t,sizeof(a))
using namespace std;
inline int read()
{
　　char ch=getchar();int x=0,f=1;
　　while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
　　while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
　　return x*f;
}
int n,m;
queue<int> p;
int head1[400010],head2[400010];
struct Edge
{
　　int to,from,next1,next2;
　　bool td;
}edge[400010];
int v2[10010],v1[10010];
int cnt;
inline void add_Edge(int from,int to)
{
　　edge[++cnt].to=to;
　　edge[cnt].from=from;
　　edge[cnt].next1=head1[from];//正向
　　edge[cnt].next2=head2[to];//反向
　　head2[to]=head1[from]=cnt;
}
bool bj[10010];
void SPFA2(int s)//反
{
　　int i;
　　for(i=1;i<=n;++i)
　　v2[i]=10100;
　　v2[s]=0,bj[s]=true,p.push(s);
　　while(p.size())
　　{
　　　　int q=p.front();p.pop();bj[q]=false;
　　　　for(i=head2[q];i;i=edge[i].next2)
　　　　{
　　　　　　int g=edge[i].from;//
　　　　　　if(v2[g]>v2[q]+1)
　　　　　　{
　　　　　　　　v2[g]=v2[q]+1;
　　　　　　　　if(!bj[g])
　　　　　　　　{
　　　　　　　　　　bj[g]=true;
　　　　　　　　　　p.push(g);
　　　　　　　　}
　　　　　　}
　　　　}
　　}
}
void SPFA1(int s)//反
{
　　int i;
　　v1[s]=0,bj[s]=true,p.push(s);
　　while(p.size())
　　{
　　　　int q=p.front();p.pop();bj[q]=false;
　　　　for(i=head1[q];i;i=edge[i].next1)
　　　　{
　　　　　　int g=edge[i].to;//
　　　　　　if(v1[g]>v1[q]+1&&v1[g]!=-1)
　　　　　　{
　　　　　　　　v1[g]=v1[q]+1;
　　　　　　　　if(!bj[g])
　　　　　　　　{
　　　　　　　　　　bj[g]=true;
　　　　　　　　　　p.push(g);
　　　　　　　　}
　　　　　　}
　　　　}
　　}
}
int main()
{
　　int i,j,k;
　　n=read(),m=read();
　　int from,to;
　　for(i=1;i<=m;++i)
　　{
　　　　from=read(),to=read();
　　　　add_Edge(from,to);
　　}
　　int st=read(),ed=read();
　　SPFA2(ed);//进入find_back
　　for(i=1;i<=n;++i)
　　if(v2[i]==10100)
　　v2[i]=-1;
　　// for(i=1;i<=n;++i)
　　// printf("%d ",v2[i]);
　　if(v2[st]==-1)
　　{
　　　　printf("-1");//不连通
　　}
　　for(i=1;i<=n;++i)//正向预处理
　　v1[i]=10100;
　　for(i=1;i<=m;++i)
　　{
　　　　if(v2[edge[i].to]==-1)
　　　　v1[edge[i].from]=v1[edge[i].to]=-1;
　　}
//******************************
　　SPFA1(st);
　　// for(i=1;i<=n;++i)
　　// printf("%d ",v1[i]);
　　//printf("%d",v1[ed]); 防作弊标识
　　return 0;

}

Writed by Gooyu

依旧是那句老话，自己打才是自己的，我这只是提供思路

推荐题目：最优贸易（一样都要正反建图）