深度剖析RQ-VAE：从向量量化到生成式推荐的语义ID技术

深度剖析RQ-VAE：从向量量化到生成式推荐的语义ID技术

引言

近年来，大规模推荐系统正经历一场深刻的范式演进，其趋势是从传统的双塔召回模型（Dual-Encoder + ANN）向更为灵活和强大的生成式检索（Generative Retrieval）范式迁移。后者借鉴了自然语言处理领域的成功经验，将推荐任务重塑为一个序列到序列的生成问题，例如，直接预测用户下一个将要交互的物品ID。

然而，这场演进面临一个核心的技术矛盾：生成模型（如Transformer）天然善于处理和生成离散的、有限的Token序列（如词汇），而现代推荐系统中的物品（Item）通常被表示为高维、连续的浮点数向量（Embedding）。如何在这两者之间架起一座高效的桥梁，成为了业界的关键挑战。

“语义ID”（Semantic ID）应运而生，它是一种将高维连续Embedding转换为离散整数序列的精妙解决方案。一个理想的语义ID不仅是紧凑的，更重要的是其本身蕴含了丰富的层次化语义信息。而残差量化变分自编码器（Residual-Quantized Variational AutoEncoder, RQ-VAE）正是当前生成高质量语义ID的核心技术之一。

本文旨在对RQ-VAE的工作原理、参数调优及工程实践进行一次全面的深度剖析。首先，我们将从其核心概念与数学背景出发，阐明其从VQ-VAE到RQ-VAE的演进逻辑。随后，在第二部分直观地展示其前向传播中数据的逐步量化，以及反向传播中基于STE（Straight-Through Estimator）和梯度解耦（detach）的精妙更新机制。最后，本文将提供一份详尽的超参数影响分析与实践中的问题诊断手册，为您在实际应用中可能遇到的问题提供清晰的指导。

一、 RQ-VAE核心原理与背景

1.1 从VQ-VAE到RQ-VAE

要理解RQ-VAE，我们必须先从其前身VQ-VAE谈起。

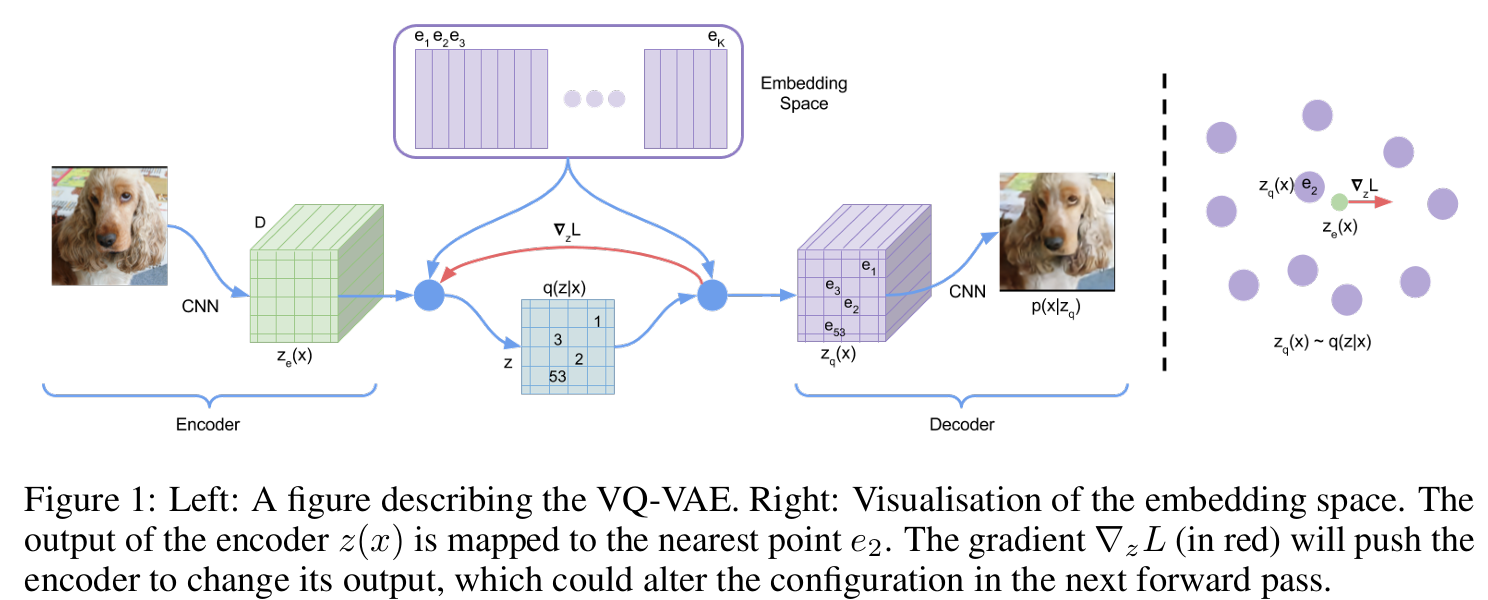
向量量化 (Vector Quantization, VQ) 的核心思想是将一个连续的、高维的向量空间，映射到一个离散的、有限的码本（Codebook）空间中。简单来说，就是为任意一个输入向量，在预设的“码本”字典里找到一个与之最相似的“码字”（Code Vector）来替代它。

VQ-VAE则将这一思想整合进了标准的自编码器（Auto-Encoder）架构中。它由三部分构成：

• 编码器 (Encoder)：将输入数据（如图片或Embedding x）压缩成一个低维的连续潜在向量zₑ。
• 量化器 (Quantizer)：通过查找码本，将zₑ替换为离它最近的码本向量z_q。这个查找操作是不可导的，因此VQ-VAE引入了梯度直通估计器（STE）来解决反向传播中的梯度中断问题。
• 解码器 (Decoder)：接收量化后的z_q，并尝试将其重建为原始输入x'。

VQ-VAE通过优化一个双重损失函数来进行训练：一是最小化x和x'之间的重建损失，以保证信息保真度；二是引入量化损失（包含码本损失和承诺损失），来让zₑ和z_q相互靠近。

然而，VQ-VAE在处理高保真度数据时面临一个瓶颈：若要精确表示复杂的输入，就需要一个极大的码本，这会带来巨大的计算和存储开销。

RQ-VAE 通过引入残差量化 (Residual Quantization) 机制完美地解决了这个问题。其核心思想是“由粗到精”的逐层逼近：

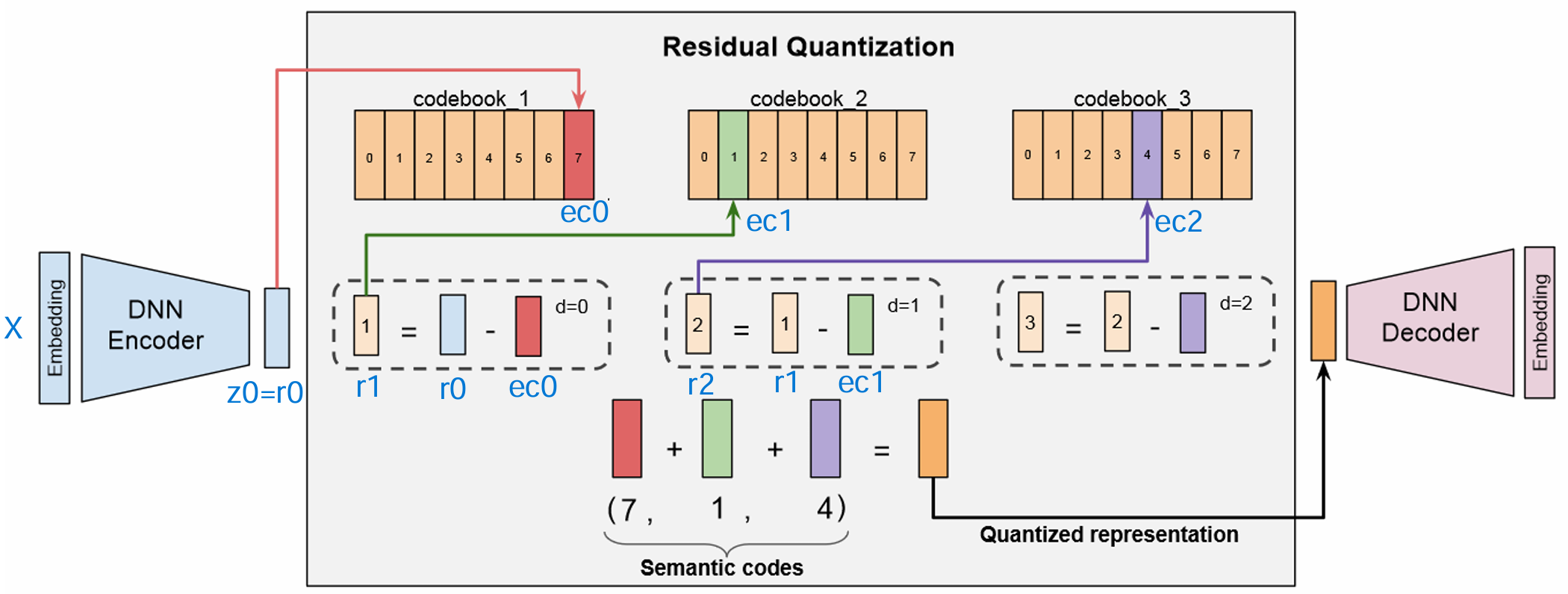
1. 第一层量化: 与VQ-VAE相同，对原始潜在向量zₑ进行一次“粗略”的量化，得到第一个码字e_c₀。
2. 计算残差: 计算原始向量与第一次量化结果之间的差值（残差）：r₁ = zₑ - e_c₀。
3. 第二层量化: 不再对原始向量进行操作，而是对残差r₁进行第二次量化，得到第二个码字e_c₁。
4. 迭代: 继续计算新的残差 r₂ = r₁ - e_c₁，并交给下一层处理。

通过这种方式，RQ-VAE将一个复杂的向量分解为一系列由粗到细的编码，极大地提升了量化精度，并自然地赋予了语义ID层次化的结构。

1.2 关键公式解析

RQ-VAE的训练目标由一个统一的损失函数来定义，该函数同样由重建损失和量化损失构成：

\[L = L_{\text{recon}} + L_{\text{vq}} \]

其中，\(L_{\text{recon}}\)通常是输入x与重建输出x_recon的均方误差（MSE）。而关键在于量化损失\(L_{\text{vq}}\)，它由每一层量化的损失累加而成。对于单层量化，其损失\(L_{\text{vq_layer}}\)定义为：

\[L_{\text{vq_layer}} = ||\text{sg}(z_e) - e||_2^2 + \beta \cdot ||z_e - \text{sg}(e)||_2^2 \]

这个公式包含了两个通过sg（stop-gradient，即代码中的.detach()）操作实现梯度解耦的关键部分：

• 码本损失 (Codebook Loss): 第一项 \(||\text{sg}(z_e) - e||_2^2\)。由于编码器输出zₑ的梯度被阻断，该项的梯度只会流向码本向量e。其作用是将码本向量e拉向它所代表的编码器输出zₑ的均值中心。

• 承诺损失 (Commitment Loss): 第二项 \(\beta \cdot ||z_e - \text{sg}(e)||_2^2\)。由于码本向量e的梯度被阻断，该项的梯度只会流向编码器输出zₑ。其作用是让编码器“承诺”其输出会靠近码本空间，以稳定训练过程。超参数β（commitment_cost）用于调节这份“承诺”的强度。

二、RQ-VAE计算图详解：前向传播与梯度流的深入剖析

前向传播图（图一）总结

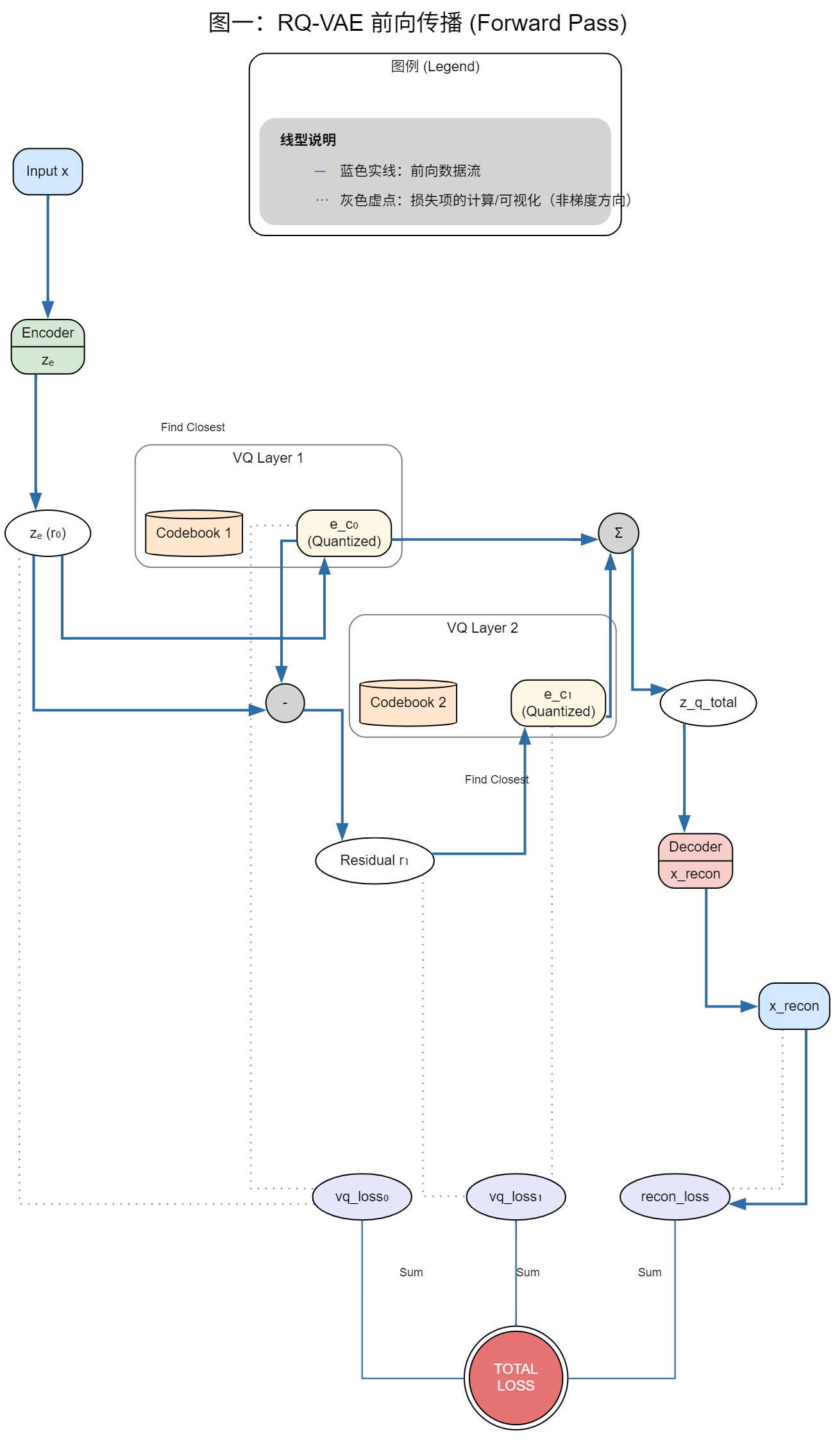
数据流向说明

前向传播遵循清晰的层级结构：

1. 输入处理：输入 x 经过 Encoder 编码得到连续表示 z_e (r₀)
2. 分层量化：
   • 第一层VQ：z_e 在 Codebook 1 中找到最近的量化向量 e_c₀
   • 残差计算：计算残差 r₁ = z_e - e_c₀
   • 第二层VQ：残差 r₁ 在 Codebook 2 中找到最近的量化向量 e_c₁
3. 重建过程：将两层量化结果聚合 z_q_total = e_c₀ + e_c₁，通过 Decoder 重建得到 x_recon
4. 损失计算：计算三种损失并求和得到总损失

反向传播图（图二）总结

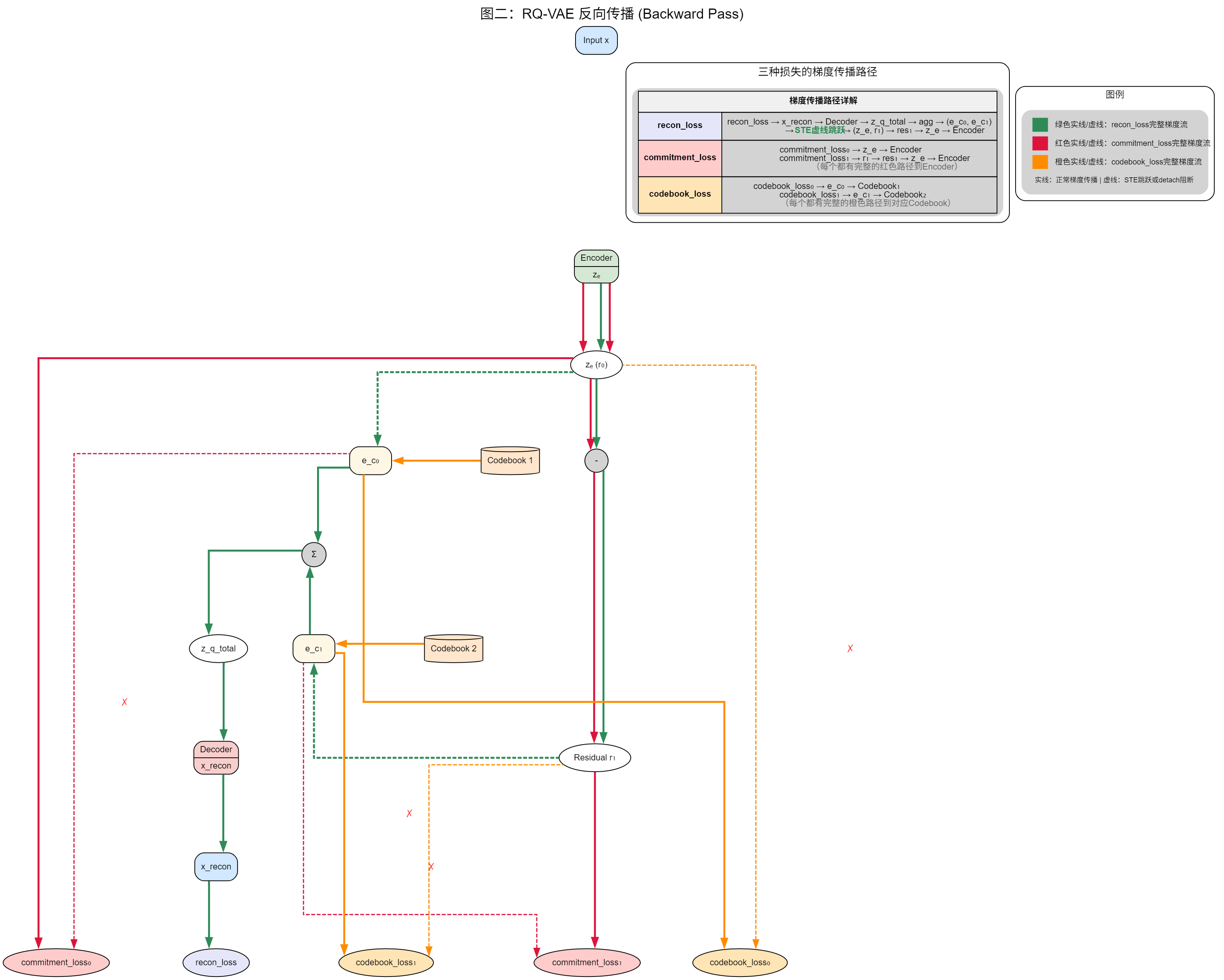
梯度流向详细说明

1. 重建损失 (recon_loss) 的梯度流

• 绿色实线路径：recon_loss → x_recon → Decoder → z_q_total → agg → (e_c₀, e_c₁)
• 绿色虚线路径（STE跳跃）：从量化向量直接跳跃到连续变量
  • e_c₀ → z_e（跳过量化操作）
  • e_c₁ → r₁（跳过量化操作）
• 绿色实线继续：r₁ → res₁ → z_e → Encoder
• 作用：这是主要的梯度流，通过STE机制使量化层可微分，最终更新Encoder和Decoder参数

2. 承诺损失 (commitment_loss) 的梯度流

• 红色实线路径：
  • commitment_loss₀ → z_e → Encoder
  • commitment_loss₁ → r₁ → res₁ → z_e → Encoder
• 红色虚线（detach阻断）：
  • commitment_loss₀ ✗→ e_c₀（被阻断）
  • commitment_loss₁ ✗→ e_c₁（被阻断）
• 作用：强制编码器输出接近量化向量，但不影响码本更新

3. 码本损失 (codebook_loss) 的梯度流

• 橙色实线路径：
  • codebook_loss₀ → e_c₀ → Codebook₁
  • codebook_loss₁ → e_c₁ → Codebook₂
• 橙色虚线（detach阻断）：
  • codebook_loss₀ ✗→ z_e（被阻断）
  • codebook_loss₁ ✗→ r₁（被阻断）
• 作用：更新码本向量接近编码器输出，但不影响编码器更新

损失对各组件的更新总结

编码器 (Encoder) 更新

• 唯二来源：recon_loss（绿色）+ commitment_loss（红色）
• 更新机制：
  • 重建损失通过STE机制传递梯度，优化重建质量
  • 承诺损失直接约束编码器输出，使其接近量化向量
• 不受影响：codebook_loss通过detach操作被阻断

解码器 (Decoder) 更新

• 唯一来源：recon_loss（绿色）
• 更新机制：直接的重建损失梯度，优化输出与输入的相似性
• 不受影响：commitment_loss和codebook_loss都不影响解码器

码本 (Codebook) 更新

• 唯一来源：codebook_loss（橙色）
• 更新机制：
  • codebook_loss₀ 更新 Codebook₁，使其向量接近对应的编码器输出
  • codebook_loss₁ 更新 Codebook₂，使其向量接近对应的残差
• 不受影响：recon_loss和commitment_loss通过detach操作被阻断

关键设计原理

1. STE机制：解决量化操作不可微的问题，使重建梯度能够传播到编码器
2. detach操作：实现梯度解耦，确保不同损失只更新特定组件
3. 分层量化：通过残差量化提高表示精度
4. 三重损失设计：重建损失保证质量，承诺损失稳定训练，码本损失优化离散表示

这种设计巧妙地解决了离散表示学习中的梯度传播问题，实现了端到端的可微分训练。

---

三、 超参数影响分析与调优指南

成功应用RQ-VAE的关键，在于理解并驾驭其众多超参数。调优过程并非简单的试错，而是在多个相互关联的目标——重建保真度、量化稳定性、和模型复杂度——之间进行权衡的艺术。本章将对核心超参数进行系统性分析，并提供实践指导。

3.1 码本相关参数

码本是量化过程的核心，其参数定义了语义ID的“词汇”体系。

• num_vq_layers (量化层数)

  • 作用: 控制残差量化的深度，即“由粗到精”的逼近过程一共进行多少轮。
  • 影响分析:
    • 增加层数: 理论上可以提升量化精度。每一附加层都致力于编码上一层的量化误差（残差），从而能够以更高的保真度表示原始潜在向量。
    • 减少层数: 降低模型复杂度和计算成本，加快训练和推理速度。
  • 调优指南: 对于多数应用场景，2至4层 提供了一个优秀的性价比平衡点。过少的层数（如1层）可能无法达到足够的表示精度，而过多的层数则会带来边际效益递减和过高的复杂性。

• num_embeddings_list (各层码本大小)

  • 作用: 定义了每一层量化“词典”的大小，即该层可供选择的码本向量（“码字”）的数量。
  • 影响分析:
    • 增大码本: 提供更丰富的“词汇量”，允许模型捕捉更细微、更多样的语义概念，拥有更高的理论表达上限。
    • 减小码本: 降低模型参数量，训练时更容易让所有码字得到充分利用。
  • 核心权衡: 主要的风险在于“码本坍塌” (Codebook Collapse)。一个过大的码本在不稳定的训练或不足的训练数据下，很容易导致编码器只学会使用其中一小部分“安全”的码字，造成大量参数浪费。
  • 调优指南: 码本大小应与特征的语义复杂度相匹配，而非物品总数。对于许多任务，每层256个码字是一个经过广泛验证的、鲁棒性很强的选择。如果特征较为简单，可以尝试128或64；如果特征极其复杂，可以探索512。

3.2 网络结构参数

编解码器是将数据在原始空间与潜在空间之间进行转换的桥梁。

• latent_dim (潜在向量维度)

  • 作用: 这是编码器的输出维度，也是量化操作发生的空间维度。它是模型中名副其实的“信息瓶颈”。
  • 影响分析:
    • 维度过小: 会导致严重的信息损失。编码器被迫丢弃过多细节，即使后续量化再完美，解码器也无法高质量地重建原始输入，最终导致重建损失过高。
    • 维度过大: 虽然能保留更多信息，但也可能让量化变得更困难（高维空间中的最近邻搜索问题），甚至使编码器“懒惰”，不对信息进行有效压缩。
  • 调优指南: latent_dim应与input_dim和数据复杂度相协调。一个8x到32x的压缩率是合理的探索起点。例如，相关研究中存在将768维输入压缩至32维的成功案例。

• Encoder/Decoder 结构 (层数与维度)

  • 作用: 定义了非线性映射函数的容量，即模型能学习多复杂的特征变换。
  • 影响分析: 更深、更宽的网络能拟合更复杂的函数。容量不足会导致欠拟合；容量过剩则会增加过拟合风险和计算成本。
  • 调优指南: 编解码器结构应保持对称，并确保维度是渐进式变化（编码器如漏斗，解码器如反向漏斗），避免维度“断崖式”升降。通常2-4个隐藏层足以应对多数任务。

3.3 训练过程参数

这些参数直接控制着模型优化的动态过程。

• learning_rate (学习率) 与 优化器

  • 作用: 控制参数更新的步长，是影响训练稳定性的最关键因素。
  • 影响分析: 过高的学习率会导致损失爆炸和码本坍塌；过低则收敛缓慢。
  • 调优指南: 对于AdamW等现代优化器，建议从一个较小的值开始，如 1e-4 到 1e-3。强烈推荐配合学习率调度器（如OneCycleLR或CosineAnnealingLR）以实现最佳性能。需要注意的是，不同的优化器（如论文中提到的Adagrad）其适用的学习率范围差异巨大，例如Adagrad可以使用高达0.4的学习率。

• commitment_cost (β, 承诺系数)

  • 作用: 这是调节编码器与码本之间“互动关系”的核心旋钮。它作为承诺损失（Commitment Loss）的权重，回答了这样一个问题：“当编码器输出zₑ与码本向量z_q不一致时，应该主要由谁来负责靠近对方？”
  • 影响分析:
    • β较低 (如 < 0.25): 对编码器的约束力较弱。编码器有更大的“自由”去学习如何映射输入，这可能有利于降低重建损失。但如果编码器输出过于“随心所欲”，可能会与码本整体疏远，导致量化困难和码本坍塌。
    • β较高 (如 > 0.25): 对编码器的约束力很强。它会产生一股强大的梯度“拉力”，迫使编码器的输出zₑ必须紧密地“吸附”到码本z_q的网格上。这通常能有效提升码本利用率，防止坍塌。但如果约束过强，可能会限制编码器的表达能力，牺牲一部分重建质量。
  • 调优指南: 0.25 是一个非常经典且鲁棒的默认值，被广泛应用于各类VQ-VAE模型中。采用从一个较低值（如0.1）“预热”到0.25的动态调度策略，是一种在实践中行之有效的进阶技巧，它允许编码器在训练初期自由探索，在后期则加强对齐约束。

• batch_size (批次大小) 与 num_epochs (训练轮数)

  • 作用: batch_size影响单次梯度更新的稳定性；num_epochs决定模型看完整份数据的总次数。
  • 影响分析: 在硬件允许的前提下，更大的批次通常能提供更稳定的梯度估计，使训练过程更平滑。训练轮数则需要足够多，以保证模型在设定的学习率下有充分的时间收敛。
  • 调优指南: 建议使用硬件显存所能支持的最大batch_size（如1024）。训练轮数不应是一个固定值，而应通过观察验证集损失是否收敛来决定。

四、 常见问题诊断与调参手册

理论的优雅最终要落地于实践的稳定。在训练RQ-VAE的过程中，几乎总会遇到各种挑战。本章旨在提供一份清晰的实践手册，帮助您诊断和解决最常见的几类问题。

4.1 问题：码本坍塌 (Codebook Collapse)

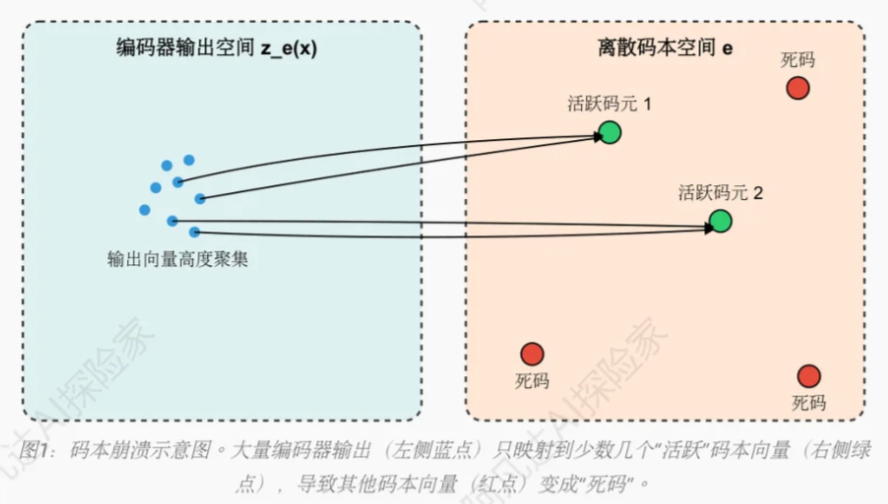
这是训练VQ-VAE/RQ-VAE时最臭名昭著的问题，必须高度警惕。

• 现象: 训练结束后，通过分析脚本发现码本利用率（Codebook Usage）极低。例如，设定的码本大小为256，但最终只有不到10%（甚至只有个位数）的码字被使用过。同时，vq_loss可能会收敛到一个异常低的值。

• 深层次原因： 码本更新机制的缺陷，每次只有一个被选中的码字能得到更新，其他的梯度都为零，就会导致其他码字得不到更新，且在码本初始化利用率就很少的情况下，就会导致码本坍塌。

• 诊断:

  1. 初始化不佳: K-Means初始化步骤未能提供一个良好的码本起始分布。
  2. 训练过程不稳定: 过高的学习率是首要元凶。它导致模型在优化过程中发生“抖动”或“崩溃”，最终收敛到一个“懒惰”的局部最优点，即编码器只输出少数几种潜在向量，因为这样做最容易降低损失。

• 解决方案:

  1. 大幅降低学习率: 这是解决训练不稳定的第一步，也是最有效的一步。将学习率调整至1e-4到1e-3的常规范围，并配合学习率调度器使用。
  2. 指数移动平均 (EMA) 更新: 通过编码器输出的移动平均值来更新码本，绕过直接的梯度下降。
  3. 引入码本重置 (Codebook Resetting): 一种更高级的技巧。在训练中周期性地检测并重置那些长期未被使用的“死亡”码字，例如，将它们重新初始化到高密度数据簇的中心附近。
  4. 减少嵌入维度，增加码本容量: 降低维度，能够减小潜在向量空间的体积来缩短“潜在向量分布”与“码本向量分布”之间的平均距离，从而让更多的码本向量有机会成为某个潜在向量的最近邻，从而进行码字更新

4.2 问题：重建损失 (Reconstruction Loss) 过高

• 现象: recon_loss在训练后期依然维持在较高的水平，无法有效降低，导致重建出的向量与原始向量差异巨大。

• 诊断: 模型在“编码-量化-解码”的完整链路中丢失了过多关键信息。

  1. 信息瓶颈过窄: latent_dim设置得太小，在量化前就已经造成了不可逆的信息损失。
  2. 模型容量不足: 编码器/解码器的网络层数太少或维度太低，不足以学习到从原始空间到潜在空间的复杂映射。
  3. 承诺系数β过高: 过强的约束力迫使编码器过度关注于对齐码本，而牺牲了对原始信息细节的保留。

• 解决方案:

  1. 增大潜在向量维度 latent_dim: 这是最直接的解决方式，拓宽了信息瓶颈。
  2. 加深/加宽编解码器网络: 增加模型的参数量和拟合能力。
  3. 降低承诺系数β: 适当减小commitment_cost，降低编码器对对齐码本的关注度，保留原始细节。

4.3 问题：量化损失 (Quantization Loss) 过高

• 现象: vq_loss（尤其是其中的commitment_loss部分）居高不下。

• 诊断: 编码器的输出分布与码本的分布始终存在较大差异，两者未能有效“会合”。

  1. 承诺系数β过低: 对编码器的“拉力”不足，无法有效引导其输出向码本靠近。
  2. 码本容量不足: 码本的“词汇量”不足以覆盖编码器输出的潜在向量分布。
  3. 初始化不佳: K-Means初始化阶段未能给码本一个良好的起点。

• 解决方案:

  1. 增大承诺系数β: 这是最直接的对策，增强编码器向码本对齐的激励。
  2. 增大码本容量: 提供更多、更丰富的码字供编码器选择。
  3. 检查并优化初始化: 确保用于K-Means初始化的数据量足够且具有代表性。

4.4 问题：训练过程不稳定

• 现象: 损失函数值在训练过程中剧烈震荡，或者突然爆炸变为一个极大的数值（或NaN）。

• 诊断:

  1. 学习率过高: 这是90%以上不稳定问题的根源。过大的更新步长使得优化过程无法稳定地走向损失函数的谷底。
  2. 梯度爆炸: 在深层网络中，梯度在反向传播过程中累积，可能变得极大。

• 解决方案:

  1. 降低学习率: 学习率股过大导致更新过于激进。
  2. 应用梯度裁剪 (Gradient Clipping): 这是一种鲁棒的技术，用于限制梯度的最大范数，防止其爆炸。
  3. 使用学习率预热 (Warm-up): 学习率调度器（如OneCycleLR）中的预热阶段，可以在训练初期使用一个很小的学习率，帮助模型稳定地“启动”，然后再逐渐增加到正常水平。
  4. 指数移动平均（EMA）更新梯度

4. 指数移动平均（EMA）更新码本

说明

EMA（Exponential Moving Average）更新是一种替代标准梯度下降来更新码本的“软更新”策略。其核心思想是让码本向量的更新过程变得极其平滑和稳定。

1. 它解决了什么问题？
在标准的梯度更新中，码本向量的位置完全由当前批次（batch）计算出的codebook_loss梯度和全局学习率决定。如果某个批次的数据分布有偏差，就可能导致码本向量发生剧烈“跳跃”。这就造成了您引文中描述的“编码器和码本互相‘追着跑’”的不稳定问题。

2. EMA是如何工作的？
EMA更新完全抛弃了codebook_loss的梯度。取而代之的是，它在每次前向传播时，都按照一个平滑的滑动平均公式来“温柔地”移动码本向量：

码本向量_新 = decay * 码本向量_旧 + (1 - decay) * 映射到该码本的zₑ向量的均值

这里的decay（衰减因子，通常设为0.99）是关键。一个高的decay值意味着码本向量极度“信任”自己过去的位置，每次只朝着新来的zₑ均值方向移动一小步。这就像一艘巨轮调整航向，缓慢而稳定，完全不受单批次数据波浪的剧烈影响。

3. 核心优势：解耦与稳定

• 解耦 (Decoupling): 码本的更新不再与全局优化器（AdamW）及其复杂的学习率调度策略（OneCycleLR）耦合。它有了自己独立的、极其简单的更新规则。
• 稳定 (Stability): 通过滑动平均，码本的演进变得非常平滑，为编码器提供了一个稳定、可预测的“靶子”，让编码器可以更安心地学习如何映射潜在空间，从而有效避免“来回拉扯”，是解决码本坍塌和训练不稳定的强大武器。

---

实现

要实现EMA更新，我们需要修改VQEmbedding类。下面是一个增加了EMA更新逻辑的新版本，我们可以称之为VQEmbeddingEMA。

class VQEmbedding(nn.Module):
    """
    单层向量量化模块，使用EMA（指数移动平均）方式更新码本。
    """
    def __init__(self, num_embeddings: int, embedding_dim: int, 
                 commitment_cost: float = 0.25, decay: float = 0.99, epsilon: float = 1e-5):
        """
        Args:
            num_embeddings: 码本中向量的数量。
            embedding_dim: 每个码本向量的维度。
            commitment_cost: commitment loss的权重。
            decay: EMA更新的衰减率，接近1.0会使更新更平滑。
            epsilon: 用于防止除以零的小常数。
        """
        super().__init__()
        self.embedding_dim = embedding_dim
        self.num_embeddings = num_embeddings
        self.commitment_cost = commitment_cost
        self.decay = decay
        self.epsilon = epsilon

        # 将码本注册为buffer，它不是一个可学习的参数，而是由EMA手动更新
        self.register_buffer('embeddings', torch.randn(num_embeddings, embedding_dim))
        
        # 用于EMA更新的缓存
        self.register_buffer('ema_cluster_size', torch.zeros(num_embeddings))
        self.register_buffer('ema_dw', torch.zeros(num_embeddings, embedding_dim))
        
        self.initialized_with_data = False

    def initialize_from_data(self, data: torch.Tensor):
        """使用K-Means对码本进行一次性初始化，避免随机初始化陷阱。"""
        if self.initialized_with_data:
            return
            
        data_np = data.detach().cpu().numpy()
        n_samples = data_np.shape[0]
        
        if n_samples < self.num_embeddings:
            # 样本不足时，有放回地抽样
            indices = np.random.choice(n_samples, self.num_embeddings, replace=True)
            centroids = data_np[indices]
        else:
            kmeans = KMeans(n_clusters=self.num_embeddings, n_init='auto', max_iter=100)
            kmeans.fit(data_np)
            centroids = kmeans.cluster_centers_
        
        # 初始化码本和EMA的向量和
        self.embeddings.data.copy_(torch.from_numpy(centroids))
        self.ema_dw.data.copy_(torch.from_numpy(centroids))
        self.initialized_with_data = True

    def forward(self, inputs: torch.Tensor):
        # 计算输入向量与码本中所有向量的欧氏距离的平方
        # inputs shape: (B, D)
        distances = (
            torch.sum(inputs**2, dim=1, keepdim=True) +
            torch.sum(self.embeddings**2, dim=1) -
            2 * torch.matmul(inputs, self.embeddings.t())
        )
        
        # 找到距离最近的码本向量的索引
        # indices shape: (B,)
        indices = torch.argmin(distances, dim=1)
        
        # 根据索引从码本中取出量化后的向量
        # quantized shape: (B, D)
        quantized = F.embedding(indices, self.embeddings)
        
        # --- EMA码本更新逻辑 (仅在训练模式下执行) ---
        if self.training:
            # 将索引转换为one-hot编码，方便进行聚合操作
            # indices_one_hot shape: (B, N), N 是 num_embeddings
            indices_one_hot = F.one_hot(indices, self.num_embeddings).to(inputs.dtype)
            
            # 1. 计算当前批次每个聚类的样本数
            # dw shape: (N,)
            dw = torch.sum(indices_one_hot, dim=0)
            
            # 2. 使用EMA更新聚类样本数
            self.ema_cluster_size.data.mul_(self.decay).add_(dw, alpha=1 - self.decay)
            
            # 3. 计算当前批次每个聚类的向量和
            # dw_sum shape: (N, D)
            dw_sum = torch.matmul(indices_one_hot.t(), inputs)
            
            # 4. 使用EMA更新聚类的向量和
            self.ema_dw.data.mul_(self.decay).add_(dw_sum, alpha=1 - self.decay)
            
            # 5. 计算更新后的码本 (加入epsilon防止除零)
            # 使用拉普拉斯平滑，避免因某个码本向量长时间未使用导致ema_cluster_size过小
            n = torch.sum(self.ema_cluster_size)
            updated_cluster_size = (
                (self.ema_cluster_size + self.epsilon) / (n + self.num_embeddings * self.epsilon) * n
            )
            
            # 标准化向量和，得到新的码本向量
            updated_embeddings = self.ema_dw / updated_cluster_size.unsqueeze(1)
            
            # 6. 将更新后的码本复制回 self.embeddings
            self.embeddings.data.copy_(updated_embeddings)

        # --- 损失计算 ---
        # EMA更新方式下，损失函数只包含commitment loss
        loss = self.commitment_cost * F.mse_loss(inputs, quantized.detach())
        
        # --- 梯度直通 (Straight-Through Estimator) ---
        # 将量化后向量的梯度直接传递给编码器的输出
        quantized = inputs + (quantized - inputs).detach()
        
        return quantized, indices, loss

完整的RQ-VAE实现代码

```python
import os
import torch
import numpy as np
import torch.nn as nn
from pathlib import Path
import torch.nn.functional as F
from sklearn.cluster import KMeans
from torch.utils.data import DataLoader
from tqdm import tqdm
import pickle
import json

# ===================================================================
# --- 1. 基础组件 (Building Blocks) ---
# 我们首先定义构成完整模型的所有独立、可复用的模块。
# ===================================================================

class RQEncoder(nn.Module):
    """
    编码器模块：
    负责将高维输入向量压缩为低维潜在表示。
    """
    def __init__(self, input_dim: int, hidden_dims: list, latent_dim: int):
        super().__init__()
        layers = []
        in_dim = input_dim
        for hidden_dim in hidden_dims:
            layers.extend([
                nn.Linear(in_dim, hidden_dim),
                nn.BatchNorm1d(hidden_dim),
                nn.ReLU()
            ])
            in_dim = hidden_dim
        layers.append(nn.Linear(in_dim, latent_dim))
        self.encoder = nn.Sequential(*layers)

    def forward(self, x):
        return self.encoder(x)

class RQDecoder(nn.Module):
    """
    解码器模块：
    负责将量化后的低维向量重建为原始维度。
    """
    def __init__(self, latent_dim: int, hidden_dims: list, output_dim: int):
        super().__init__()
        layers = []
        in_dim = latent_dim
        for hidden_dim in reversed(hidden_dims):
            layers.extend([
                nn.Linear(in_dim, hidden_dim),
                nn.BatchNorm1d(hidden_dim),
                nn.ReLU()
            ])
            in_dim = hidden_dim
        layers.append(nn.Linear(in_dim, output_dim))
        self.decoder = nn.Sequential(*layers)

    def forward(self, x):
        return self.decoder(x)

class VQEmbedding(nn.Module):
    """
    单层向量量化模块 (Vector Quantization Embedding)。
    包含一个码本 (codebook)，负责将输入向量映射到码本中最接近的向量。
    """
    def __init__(self, num_embeddings: int, embedding_dim: int, commitment_cost: float = 0.25):
        super().__init__()
        self.num_embeddings = num_embeddings
        self.embedding_dim = embedding_dim
        self.commitment_cost = commitment_cost
        
        # 将码本注册为可学习的参数
        self.embeddings = nn.Parameter(torch.randn(num_embeddings, embedding_dim))
        self.initialized_with_data = False
        
    def initialize_from_data(self, data: torch.Tensor):
        """使用K-Means对码本进行一次性初始化，避免随机初始化陷阱。"""
        if self.initialized_with_data:
            return
            
        data_np = data.detach().cpu().numpy()
        n_samples = data_np.shape[0]
        
        if n_samples < self.num_embeddings:
            # 样本不足时，有放回地抽样
            indices = np.random.choice(n_samples, self.num_embeddings, replace=True)
            centroids = data_np[indices]
        else:
            kmeans = KMeans(n_clusters=self.num_embeddings, n_init='auto', max_iter=100)
            kmeans.fit(data_np)
            centroids = kmeans.cluster_centers_
        
        self.embeddings.data.copy_(torch.from_numpy(centroids))
        self.initialized_with_data = True

    def forward(self, inputs: torch.Tensor):
        distances = (
            torch.sum(inputs**2, dim=1, keepdim=True) +
            torch.sum(self.embeddings**2, dim=1) -
            2 * torch.matmul(inputs, self.embeddings.t())
        )
        
        indices = torch.argmin(distances, dim=1)
        quantized = F.embedding(indices, self.embeddings)
        
        # 计算损失
        codebook_loss = F.mse_loss(quantized, inputs.detach())
        commitment_loss = F.mse_loss(inputs, quantized.detach()) * self.commitment_cost
        total_loss = codebook_loss + commitment_loss
        
        # Straight-Through Estimator (梯度直通)
        quantized = inputs + (quantized - inputs).detach()
        
        return quantized, indices, total_loss

class ResidualVQ(nn.Module):
    """
    残差向量量化 (Residual Vector Quantization)。
    包含多个VQEmbedding层，对前一层的残差进行逐层量化。
    """
    def __init__(self, num_layers: int, num_embeddings_list: list, embedding_dim: int, commitment_cost: float = 0.25):
        super().__init__()
        self.num_layers = num_layers
        self.vq_layers = nn.ModuleList([
            VQEmbedding(num_embeddings_list[i], embedding_dim, commitment_cost)
            for i in range(num_layers)
        ])
        
    def initialize_from_data(self, data: torch.Tensor):
        """逐层初始化所有码本。"""
        residual = data.clone()
        for i, vq_layer in enumerate(self.vq_layers):
            print(f"[INFO] Initializing codebook layer {i+1}/{self.num_layers}...")
            vq_layer.initialize_from_data(residual)
            with torch.no_grad():
                quantized, _, _ = vq_layer(residual)
                residual -= quantized
                
    def forward(self, inputs: torch.Tensor, commitment_cost: float = None):
        residual = inputs
        quantized_total = torch.zeros_like(inputs)
        indices_list = []
        loss_total = 0.0
        
        for vq_layer in self.vq_layers:
            # 支持动态传入commitment_cost
            if commitment_cost is not None:
                vq_layer.commitment_cost = commitment_cost
            
            quantized, indices, loss = vq_layer(residual)
            residual = residual - quantized             # 会创建新张量,反向传播需要用到未被修改前的值
            quantized_total = quantized_total + quantized
            indices_list.append(indices)
            loss_total += loss
            
        return quantized_total, torch.stack(indices_list, dim=1), loss_total

# ===================================================================
# --- 2. 整合模型 (The Main Model) ---
# 使用上面定义的基础组件，拼装成完整的RQ-VAE模型。
# ===================================================================

class RQVAE(nn.Module):
    """
    完整的残差量化变分自编码器 (RQ-VAE) 模型。
    通过组合RQEncoder, ResidualVQ, 和RQDecoder模块构建。
    """
    def __init__(self, input_dim: int, hidden_dims: list, latent_dim: int,
                 num_vq_layers: int, num_embeddings_list: list, commitment_cost: float = 0.25):
        super().__init__()
        
        self.encoder = RQEncoder(input_dim, hidden_dims, latent_dim) 
        self.vq = ResidualVQ(num_vq_layers, num_embeddings_list, latent_dim, commitment_cost)
        self.decoder = RQDecoder(latent_dim, hidden_dims, output_dim=input_dim)
        
    def encode(self, x: torch.Tensor) -> torch.Tensor:
        """编码输入到潜在空间。"""
        return self.encoder(x)
        
    def decode(self, z_q: torch.Tensor) -> torch.Tensor:
        """从量化后的潜在表示解码。"""
        return self.decoder(z_q)
        
    def forward(self, x: torch.Tensor, commitment_cost: float = None):
        """完整的前向传播过程。"""
        z_e = self.encode(x)
        z_q, indices, vq_loss = self.vq(z_e, commitment_cost)
        x_recon = self.decode(z_q)
        
        recon_loss = F.mse_loss(x_recon, x)
        total_loss = recon_loss + vq_loss

        loss_dict = {
            'total': total_loss,
            'recon': recon_loss,
            'vq': vq_loss
        }
        
        return x_recon, indices, loss_dict
        
    @torch.no_grad()
    def get_semantic_ids(self, x: torch.Tensor) -> torch.Tensor:
        """(推理时使用) 获取输入的语义ID。"""
        self.eval()
        z_e = self.encode(x)
        _, indices, _ = self.vq(z_e)
        return indices
        
    def initialize_codebooks(self, dataloader, device, max_samples=100000):
        """使用数据集初始化所有码本，这是训练前的关键步骤。"""
        print("\n[IMPORTANT] Collecting data for codebook initialization...")
        init_data_list = []
        total_samples = 0
        
        # 切换到评估模式，关闭BN等层的训练行为
        self.encoder.eval()
        with torch.no_grad():
            for batch in tqdm(dataloader, desc="Collecting data"):
                # 兼容多种DataLoader输出格式
                emb_batch = batch[1] if isinstance(batch, (list, tuple)) else batch
                emb_batch = emb_batch.to(device)
                
                z_e = self.encoder(emb_batch)
                init_data_list.append(z_e.cpu())
                
                total_samples += z_e.shape[0]
                if total_samples >= max_samples:
                    break
        
        init_data = torch.cat(init_data_list, dim=0)
        init_data = init_data.to(device)
        self.vq.initialize_from_data(init_data)
        print("[SUCCESS] All codebooks initialized with data.")