中国剩余定理

中国剩余定理

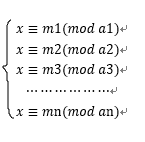
中国剩余定理，求的是模线性方程组的通解

例题

人有体力、情商、智商的高峰日子，它们分别每隔23天、28天和
33天出现一次。对于每个人，我们想知道何时三个高峰落在同一
天。给定三个高峰出现的日子p,e和i（不一定是第一次高峰出现
的日子）,再给定另一个指定的日子d，你的任务是输出日子d
之后，下一次三个高峰落在同一天的日子（用距离d的天数表示
）。例如：给定日子为10，下次出现三个高峰同一天的日子是12
，则输出2。

输入：
输入四个整数：p, e, i和d。 p, e, i分别表示体力、情感和智力
高峰出现的日子。d是给定的日子，可能小于p, e或 i。所有给
定日子是非负的并且小于或等于365，所求的日子小于或等于
21252。

输出：
从给定日子起，下一次三个高峰同一天的日子（距离给定日子
的天数）

样例：
输入样例
0 0 0 0
0 0 0 100
5 20 34 325
4 5 6 7
283 102 23 320
203 301 203 40
-1 -1 -1 -1
输出样例
Case 1: the next triple peak occurs in 21252 days.
Case 2: the next triple peak occurs in 21152 days.
Case 3: the next triple peak occurs in 19575 days.
Case 4: the next triple peak occurs in 16994 days.
Case 5: the next triple peak occurs in 8910 days.
Case 6: the next triple peak occurs in 10789 days.

思路：

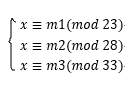
模板：

#include <iostream>
using namespace std;

int exgcd(int a, int b, int &x, int &y)
{
    if(b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    int r = exgcd(b, a%b, x, y);
    int t = x;
    x = y;
    y = t - a / b * y;
    return r;
}

int CRT(int a[], int m[], int n)
{
    int M = 1;
    for(int i=1; i<=n; i++)
    {
        M *= m[i];
    }
    for(int i=1; i<=n; i++)
    {
        int x, y;
        int Mi = M / m[i];
        exgcd(Mi, m[i], x, y);
        x = (x % b[i] + b[i]) % b[i];
        ans = (ans + a[i] * x * Mi) % M;
    }
    return (ans % M + M) % M;
}

int main()
{
    return 0;
}