题解-Ehab's REAL Number Theory Problem
Ehab's REAL Number Theory Problem
前置知识
质数
分解质因数
无向无权图最小环<讲>
给 \(n\) 个数 \(a_i\)（\(a_i\) 的因数个数不超过 \(7\)），求最少选出多少个数，使得乘积为完全平方。无解输出 \(-1\)。
数据范围：\(1\le n\le 10^5\)，\(1\le a_i\le 10^6\)。
没想到一场普通的 \(\texttt{CF}\) 比赛能出出这么毒瘤好的题！
很明显，把每个 \(a_i\) 的平方因子除尽后对答案没有影响，所以可以把每个 \(a_i\) 的平方因子除尽。
如果某个 \(a_i\) 的质因子除尽后为 \(1\)，直接选它便解决了问题。
然后剩下的质因子的幂次肯定为 \(1\)。
而且最多只有两个质因子，因为如果 \(a_i\) 有三个质因子，按照约数个数定理，\(d(a_i)=(1+1)^3=8>7\)，矛盾。
最后问题简化为，选最少的数，使乘积包含的质因子幂次都为 2（可以自己想为什么不需要选幂次为 \(4\)）。
过程：
\[18=2\times 3^2\to 2 \]
有一个极其巧妙的方法是建一个图，节点是质数，然后把每个数转换为它的两个质因子之间的一条边，求最小环。
如果某个数 \(a_i\) 质因数个数为 \(1\)（不存在为 \(0\) 的，因为已经满足方案），把 \(1\) 也看做质数节点，连 \(1\) 和 \(a_i\)。
根据环的性质，每个点的度为 \(2\)，所以边对应的数的乘积每个质因子幂次都为 \(2\)。
边没有长度，是无向边，所以问题又简化为了求无向无权图最小环。
过程：
\(a_i\)：2 3 6 15。
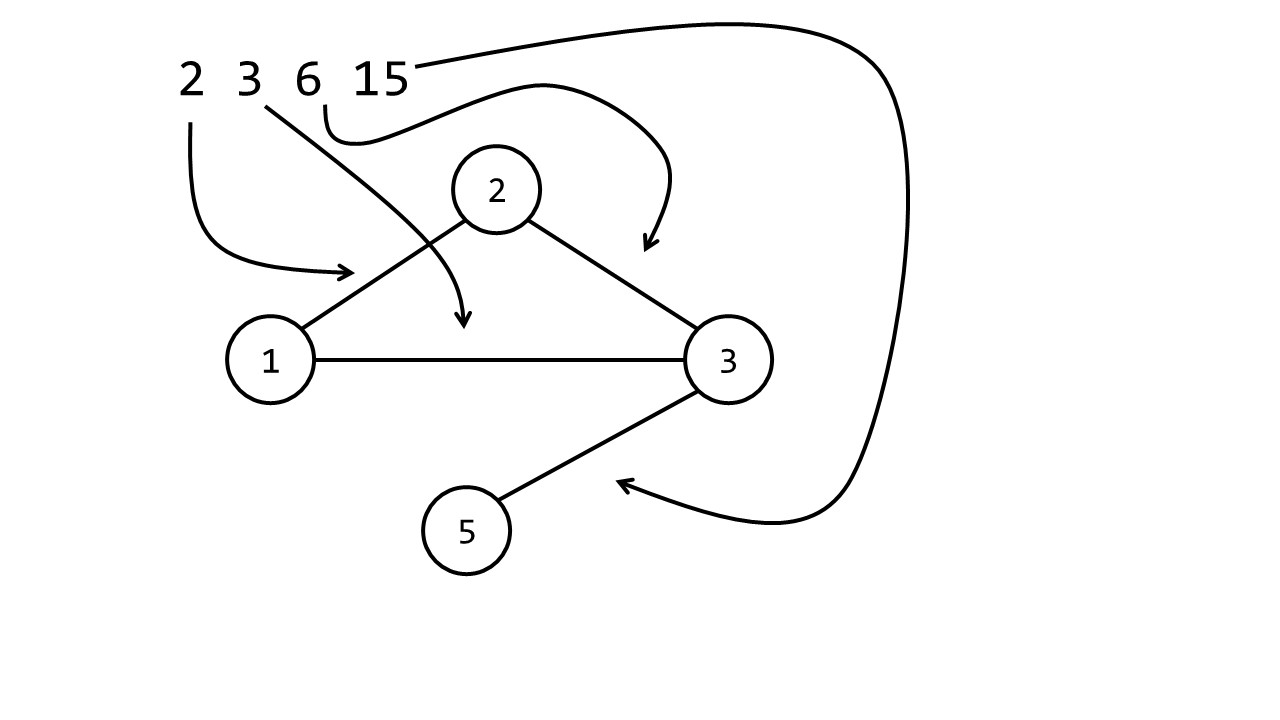
最小环为 \((1,2,3)\)。
无向无权图最小环使不得 \(\texttt{Floyd}\)！这里的点数最大约是 \(78500\)，\(\Theta(n^3)\) 能跑到射手座去了。
可以枚举起点，然后 \(\texttt{Bfs}\)，因为问题特殊，所以可以有很大优化。
因为 \(1\le a_i\le 10^6\)，所以每个 \(a_i\) 对应的边不可能连接两个 \(>1000\) 的质数。
所以如果有环，那么环必然有一个起点对应的质数 \(\in[1,1000]\)。
所以可以枚举这个起点 \(s\)，然后 \(\texttt{Bfs}\)。
设 \(dep_x\) 表示节点 \(x\) 的深度，所以 \(dep_s=0\)。每次 \(Bfs\) 前清空。
然后沿着队列顶的点 \(x\) 连的边走如果走到一个 \(dep\) 未赋值的节点 \(to\)，就令 \(dep_{to}=dep_x+1\)。
如果走到一个已经遍历过的点，那么说明这里有一个环，令 \(ans=\min\{ans,dep_{to}+dep_x+1\}\)。
\(\texttt{Bfs}\) 过程中可以走重复的点，不能走重复的边。
这里有一个问题：如何知道这个环是否以 \(s\) 为其中一个起点呢？
答案是不需要知道，无论 \(s\) 在不在环上都直接 \(ans=\min\{ans,dep_{to}+dep_x+1\}\)。
因为如果 \(s\) 不在环上，\(dep_{to}+dep_x+1\) 肯定比 \(s\) 在环上大（别忘了每个 \(s\) 都要枚举过去的啊！）。
时间复杂度 \(\Theta(n \sqrt n)\)。
过程：
只展示 \(s=1\) 的 \(\texttt{Bfs}\) 过程：
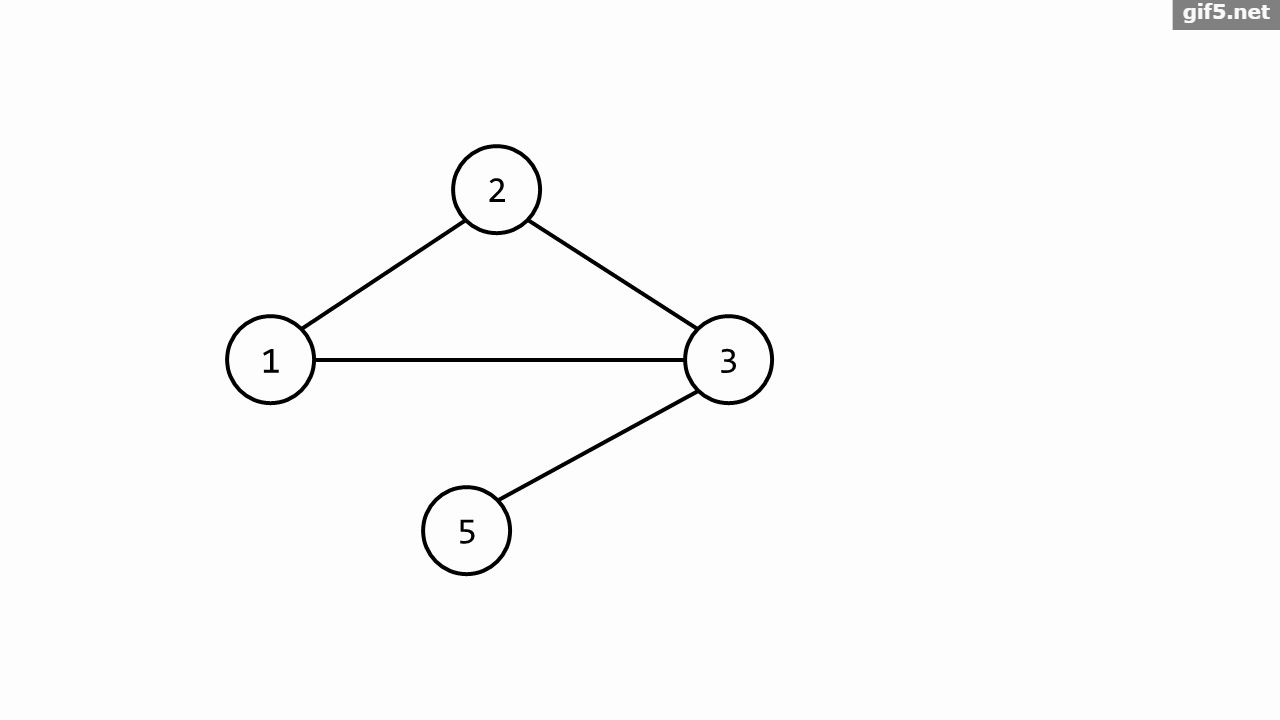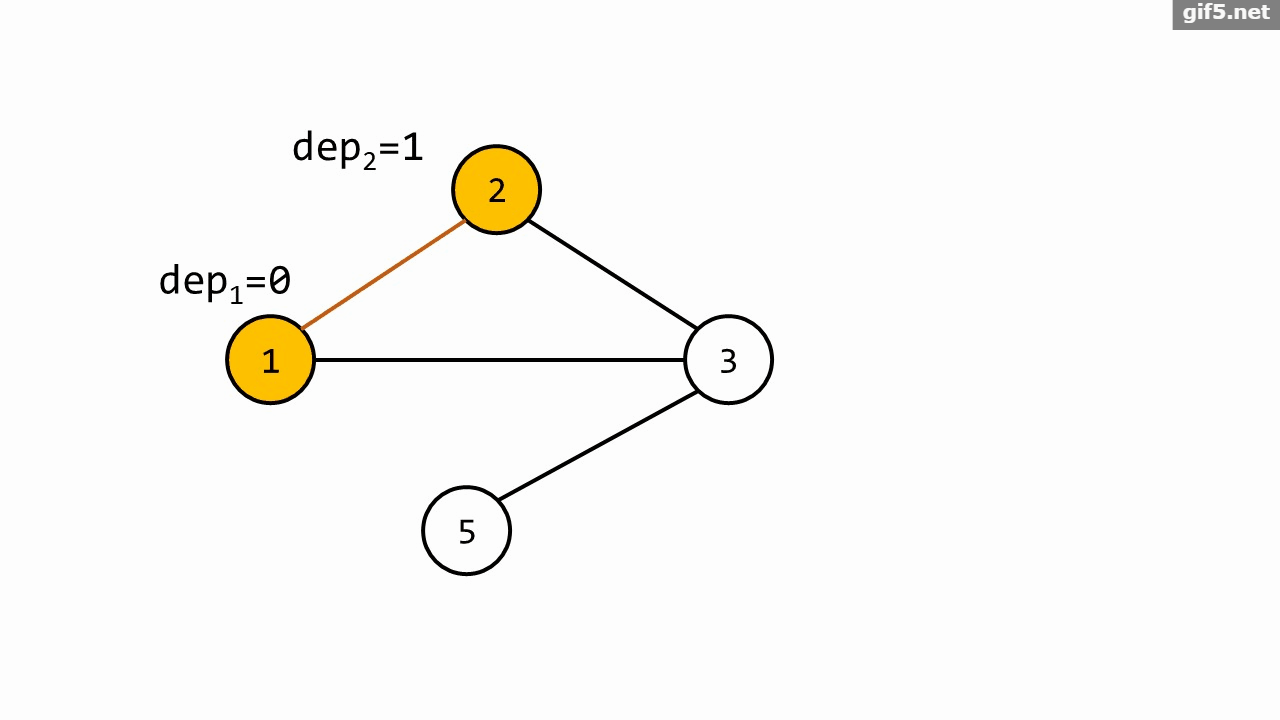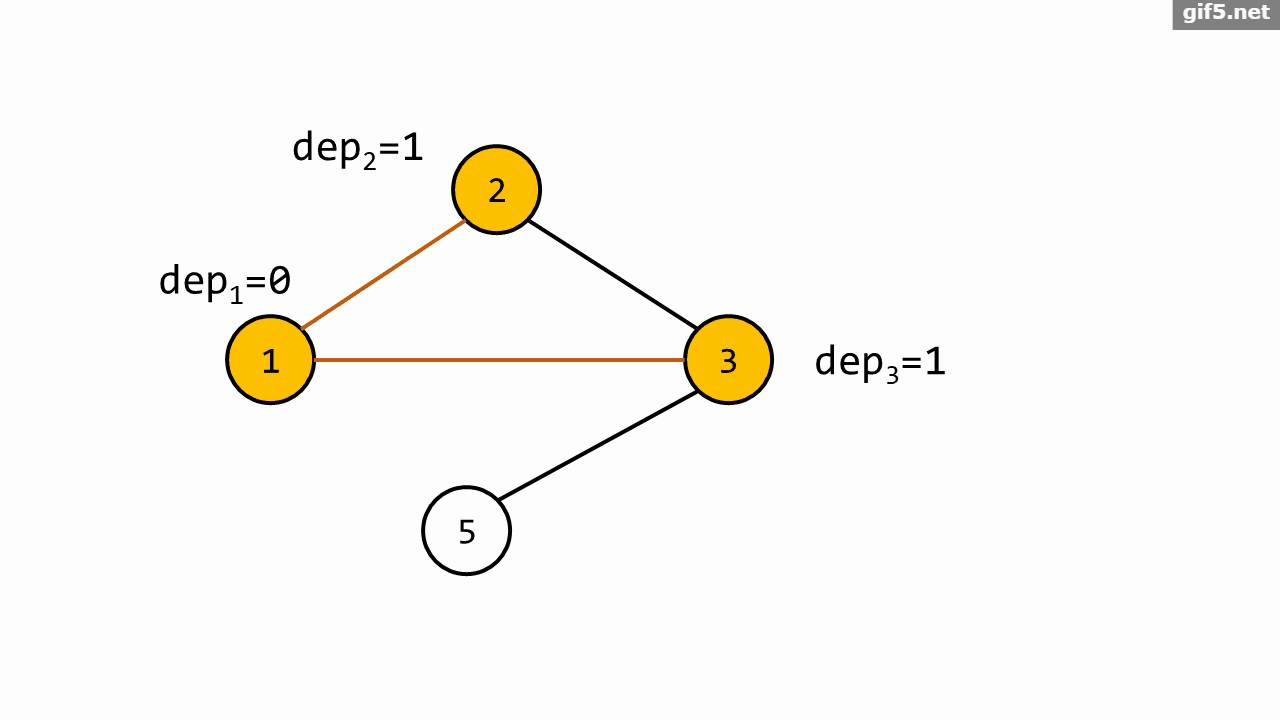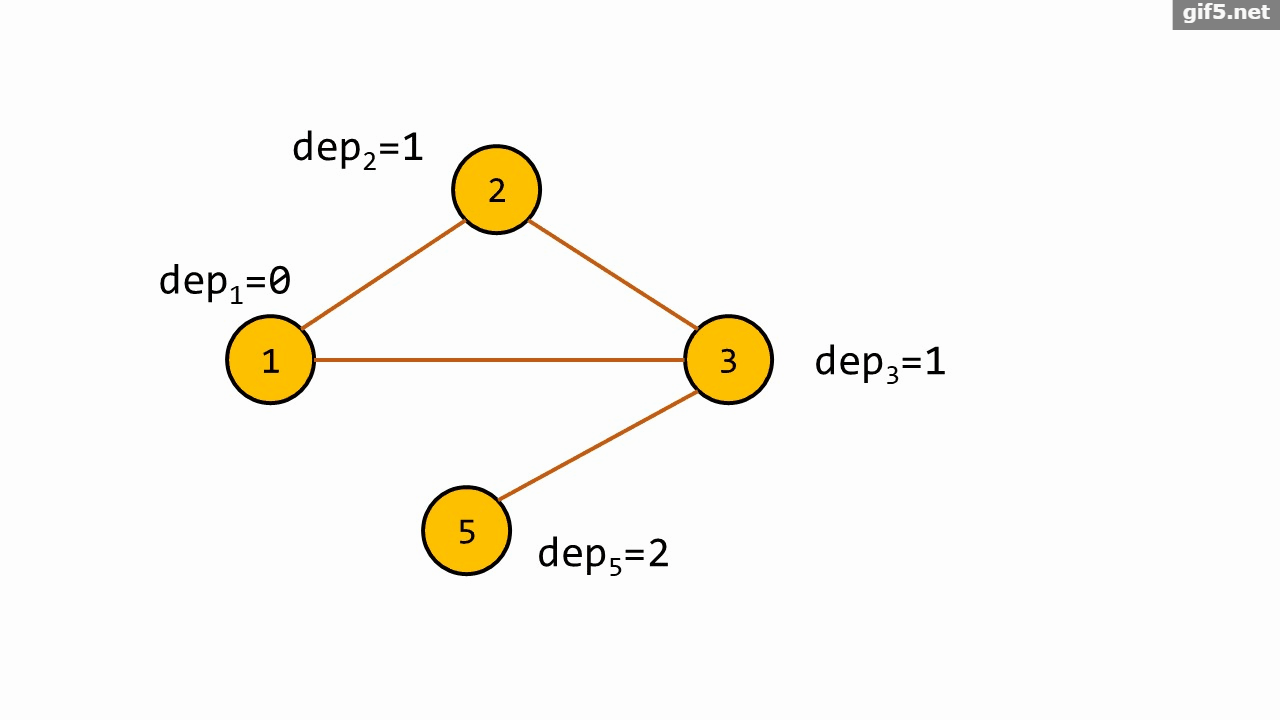
代码实现的时候，可以把质数离散化一下。
\(\texttt{code}\)
#include <bits/stdc++.h>
using namespace std;
//&Start
#define inf 0x3f3f3f3f
#define re register
#define il inline
typedef long long lng;
typedef vector<int> veci;
//&Data
#define N 100000
#define MX 1000000
#define P 78500--->1000000内质数数量
int n,a[N+10];
//&Prime--->筛质数
bitset<MX+10> np;
int p[P+10],ip[MX+10],pcnt,S;
il void Prime(){
np[1]=true,ip[1]=p[++pcnt]=S=1;
for(re int i=2;i<=MX;i++){
if(!np[i]) p[++pcnt]=i,ip[i]=pcnt,S+=(i<=999);
for(re int j=1;j<=pcnt&&i*p[j]<=MX;j++)
np[i*p[j]]=1;
}
}
//&Graph
veci e[P+10];
int E=1,to[(N<<1)+10];//---->同网络流思想，使互为反边的两条边通过^1可得
il void add(re int x,re int y){ //加双向边
e[x].push_back(++E),to[E]=y;
e[y].push_back(++E),to[E]=x;
}
il void Add(re int x){ // 把数转换为边
re int dcnt=0,div[4];
for(re int j=2;j<=pcnt&&p[j]*p[j]<=x;j++)
if(x%p[j]==0){
while(x%(p[j]*p[j])==0) x/=(p[j]*p[j]);
if(x%p[j]==0) div[++dcnt]=j,x/=p[j];
}
if(x>1) div[++dcnt]=ip[x],x=1;
if(dcnt==0) puts("1"),exit(0);
else if(dcnt==1) add(1,div[1]);
else add(div[1],div[2]);
}
int sz=inf,q[P+10][2],dep[P+10];
il void Bfs(re int s){ //以s为起点Bfs
fill(dep+1,dep+P+1,inf);
re int qcnt=0;
q[++qcnt][1]=s,dep[s]=0;
for(re int ft=1;ft<=qcnt;ft++){
re int x=q[ft][1],f=q[ft][0];
for(re int i:e[x])if(i!=(f^1)){
if(dep[to[i]]==inf){
dep[to[i]]=dep[x]+1;
q[++qcnt][1]=to[i];
q[qcnt][0]=i;
} else sz=min(sz,dep[x]+dep[to[i]]+1); //找到环
}
}
}
//&Main
int main(){
Prime();
scanf("%d",&n);
for(re int i=1;i<=n;i++)
scanf("%d",a+i),Add(a[i]);
for(re int i=1;i<=S;i++) Bfs(i); //枚举起点
if(sz==inf) puts("-1");
else printf("%d\n",sz);
return 0;
}
祝大家学习愉快！
