随笔分类 - 题解
题解
摘要：$Q$ 组测试数据。给一棵树大小为 $n$，求有多少个子树与其重心相同。重心可能有多个。
数据范围：$1\le Q\le 50$，$1\le n\le 200$。
阅读全文
摘要：给 $n$ 点 $m$ 边的带权有向图，边 $i$ 为 $(u_i,v_i,w_i)$。$q$ 次询问，每次给 $x_i$，问修改一些边使整张图的边权和增加 $x_i$ 后最短路最大值（可以把边权修改为浮点数）。
数据范围：$2\le n\le 50$，$1\le m\le n\cdot (n-1)$，$1\le u_i,v_i\le n$，$1\le w_i\le 10^6$，$1\le q\le 10^5$，$0\le x_i\le 10^5$。
阅读全文
摘要：给树 $T=(V,E)(|V|=n)$，树高为 $h$，$w_u(u\in V)$。求 $x\in V,y\in V:\left(\sum_{u\in V}w_u\cdot \min(dis_{u,x},dis_{u,y})\right)_{\min}$。
数据范围：$1\le n\le 50000$，$1\le h\le 100$。
阅读全文
摘要：CF643G Choosing Ads \(n\) 和 \(m\) 和 \(p\) 和序列 \(a_i(1\le i\le n)\)。\(m\) 种如下操作： 1 l r id 令 \(i\in[l,r]:a_i=id\)。 2 l r 输出至多 \(\lfloor\frac{100}{p}\rfl
阅读全文
摘要：$n$ 和 $m$ 和 $k$ 和序列 $b_i(1\le i\le m,1\le b_i\le b_{i+1}\le \frac n2)$。对于字符串 $s$，如果选其 $b_i$ 前缀和 $b_i$ 后缀翻转并交换能变成字符串 $s'$，则 $s,s'$ 是相等的。求有多少个长度为 $n$ 的字符串，字符集大小为 $k$，互不相等。答案 $\bmod 998244353$。
数据范围：$2\le n\le 10^9$，$1\le m\le \min(\frac n2,2\cdot 10^5)$，$1\le k\le 10^9$。
阅读全文
摘要：$n$ 和 $k$ 和 $n$ 个数的序列 $a$。把 $a$ 中的 $-1$ 替换成 $[1,k]$ 之间的整数。求使 $a$ 中不存在长度为奇数的回文串的方案数。
数据范围：$2\le n,k\le 2\cdot 10^5$，$a_i=-1{\rm~or~}a_i\in[1,k]$。
阅读全文
摘要：有一个 $n\times m$ 的矩阵 $a(1\le a_{i,j}\le p)$，求从起点 $(1,1)$ 出发依次遍历值为 $1\to p$ 的矩阵单元的最短路径曼哈顿距离。保证满足 $a_{i,j}=p$ 的 $(i,j)$ 唯一。
数据范围：$1\le n,m\le 300$，$1\le p\le n\cdot m$。
阅读全文
摘要：字符串 $s$ 和 $t$ 和 $k$。如果 $t=0$，不同位置的相同子串算 $1$ 个；如果 $t=1$，不同位置的相同子串算多个。求 $k$ 小子串，如果不存在输出 $-1$。
数据范围：$1\le n\le 5\cdot 10^5$，$t\in\{0,1\}$，$1\le k\le 10^9$。
阅读全文
摘要：$T$ 组测试数据。求字符串 $s$ 的所有子串拆成 $AABB$ 形式的方案总和。
数据范围：$1\le T\le 10$，$1\le n\le 3\cdot 10^4$。
阅读全文
摘要：https://www.luogu.com.cn/problem/CF1239D
阅读全文
摘要：给定长度为 $n$ 的初始文本 $s$，有 $m$ 个如下操作：
1. $\texttt{I x c}$，在第 $x$ 个字母后面插入一个 $c$。
2. $\texttt{D x}$，删除第 $x$ 个字母。
3. $\texttt{R x y}$，反转当前文本中的区间 $[x,y]$。
4. $\texttt{P x}$，输出初始文本中第 $x$ 个字母在当前文本中的位置。特别地，若不存在，输出 $0$。
5. $\texttt{T x}$，输出当前文本中第 $x$ 个字母。
6. $\texttt{Q x y}$，输出当前文本中区间 $[x,y]$ 内出现过的字母的种类数。
数据范围：$1\le n,m\le 10^5$。
阅读全文
摘要：$T$ 组数据，每次给定 $p$，求
$$\left(2^{\left(2^{\left(2^{\cdots}\right)}\right)}\right)\bmod p$$
数据范围：$1\le T\le 1000$，$1\le p\le 10^7$。
阅读全文
摘要：
Quantifier Question
https://www.luogu.com.cn/problem/CF1344C
阅读全文
Quantifier Question
https://www.luogu.com.cn/problem/CF1344C
阅读全文
摘要：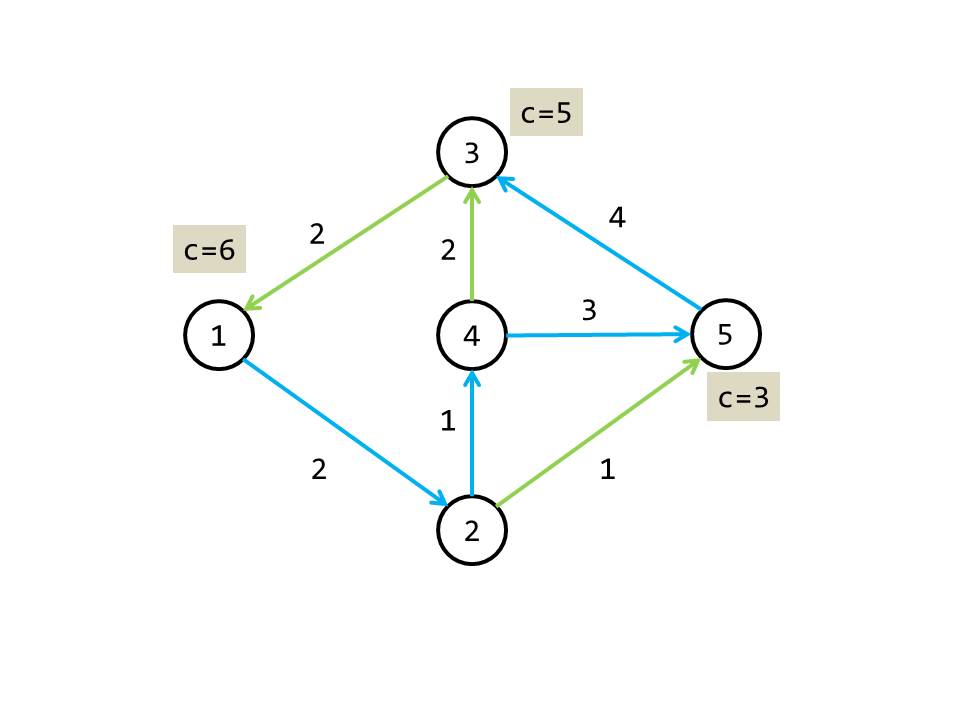
给一个 $n$ 个点 $m$ 条边（权值为 $d_i$）的无向有权图，可能有重边和子环。可以多次经过一条边，求 $1\to n$ 的路径的最大边权异或和。
数据范围：$1\le n\le 5\cdot 10^4$，$1\le m\le 10^5,0\le d_i\le 10^{18}$。
阅读全文
给一个 $n$ 个点 $m$ 条边（权值为 $d_i$）的无向有权图，可能有重边和子环。可以多次经过一条边，求 $1\to n$ 的路径的最大边权异或和。
数据范围：$1\le n\le 5\cdot 10^4$，$1\le m\le 10^5,0\le d_i\le 10^{18}$。
阅读全文
摘要：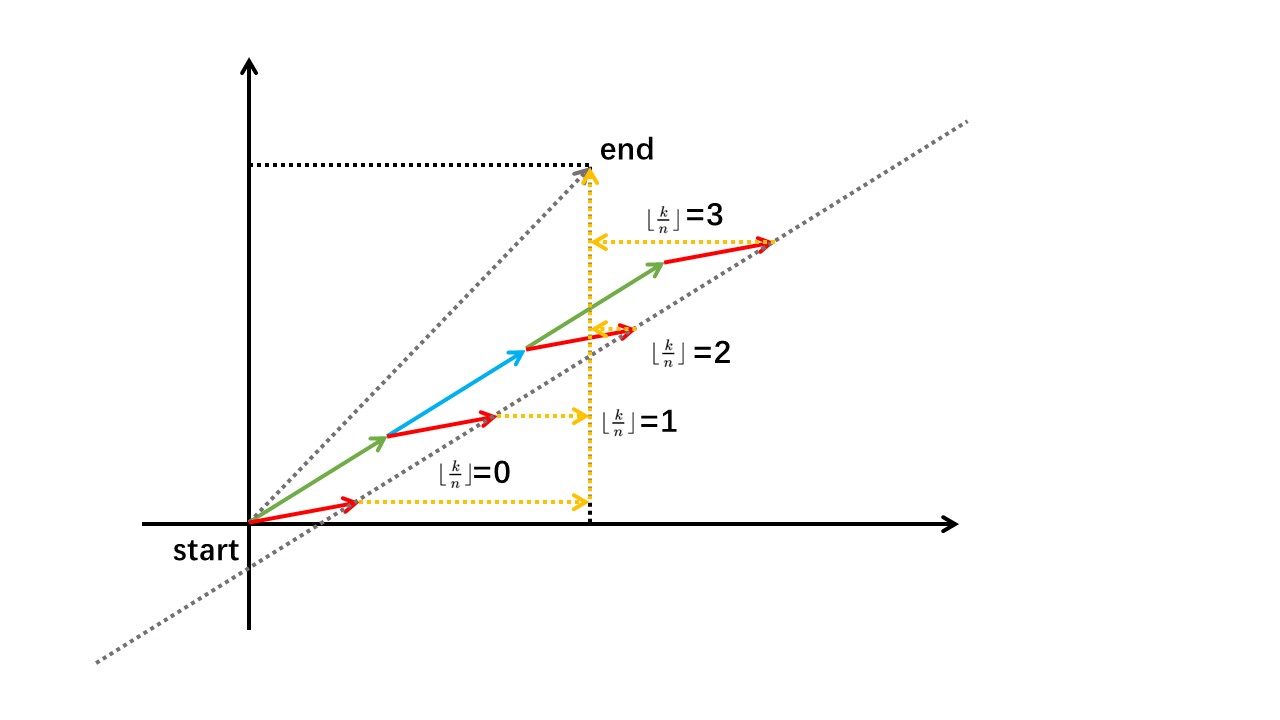
你在 $(x_1,y_1)$，要到点 $(x_2,y_2)$。风向周期为 $n$，一个字符串 $s\{n\}$ 表示风向（每轮上下左右），每轮你都会被风向吹走一格。你可以在被风吹得被动移动的基础上选择每轮移动一格或不移动。求最少几轮可以到达终点。
数据范围：$0\le x_1,y_1,x_2,y_2\le 10^9$，$1\le n\le 10^5$。
阅读全文
你在 $(x_1,y_1)$，要到点 $(x_2,y_2)$。风向周期为 $n$，一个字符串 $s\{n\}$ 表示风向（每轮上下左右），每轮你都会被风向吹走一格。你可以在被风吹得被动移动的基础上选择每轮移动一格或不移动。求最少几轮可以到达终点。
数据范围：$0\le x_1,y_1,x_2,y_2\le 10^9$，$1\le n\le 10^5$。
阅读全文
摘要：
求序列 $a\{n\}$ 中的三元逆序对数量。
数据范围：$3\le n\le 1e6$。
阅读全文
求序列 $a\{n\}$ 中的三元逆序对数量。
数据范围：$3\le n\le 1e6$。
阅读全文
摘要：
有 $n$ 个桥墩，高 $h_i$ 重 $w_i$。连接 $i$ 和 $j$ 消耗代价 $(h_i-h_j)^2$，用不到的桥墩被拆除，代价为 $w_i$。求使 $1$ 与 $n$ 联通的最小代价。
数据范围：$2\le n\le 10^5$，$0\le h_i,|w_i|\le 10^6$。
阅读全文
有 $n$ 个桥墩，高 $h_i$ 重 $w_i$。连接 $i$ 和 $j$ 消耗代价 $(h_i-h_j)^2$，用不到的桥墩被拆除，代价为 $w_i$。求使 $1$ 与 $n$ 联通的最小代价。
数据范围：$2\le n\le 10^5$，$0\le h_i,|w_i|\le 10^6$。
阅读全文
摘要：
FFT 的第一道练习题。蒟蒻祝自己变强。
阅读全文
FFT 的第一道练习题。蒟蒻祝自己变强。
阅读全文
摘要：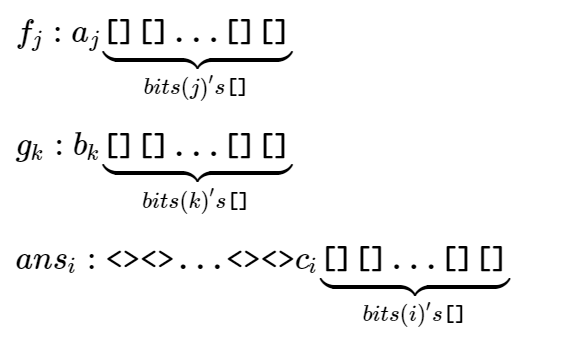
给定 $n$ 和序列 $a_0,a_1,\dots,a_{2^n-1}$ 和 $b_0,b_1,\dots,b_{2^n-1}$，求序列 $c_0,c_1,\dots,c_{2^n-1}$ 满足 $$c_i=\left(\sum_{j|k=i,j\&k=0} a_j\cdot b_k\right)\bmod 4$$ 数据范围：$a_i,b_i\in[0,3]$，$0\le n\le 21$。
阅读全文
给定 $n$ 和序列 $a_0,a_1,\dots,a_{2^n-1}$ 和 $b_0,b_1,\dots,b_{2^n-1}$，求序列 $c_0,c_1,\dots,c_{2^n-1}$ 满足 $$c_i=\left(\sum_{j|k=i,j\&k=0} a_j\cdot b_k\right)\bmod 4$$ 数据范围：$a_i,b_i\in[0,3]$，$0\le n\le 21$。
阅读全文
摘要：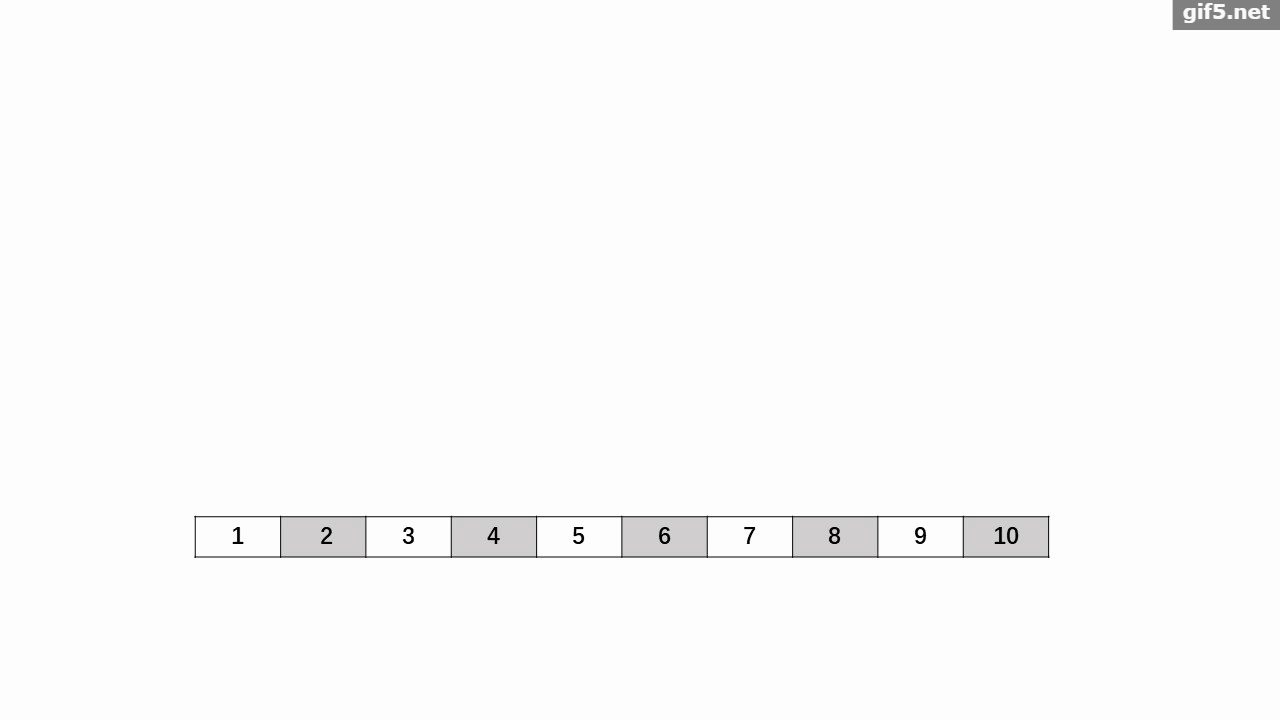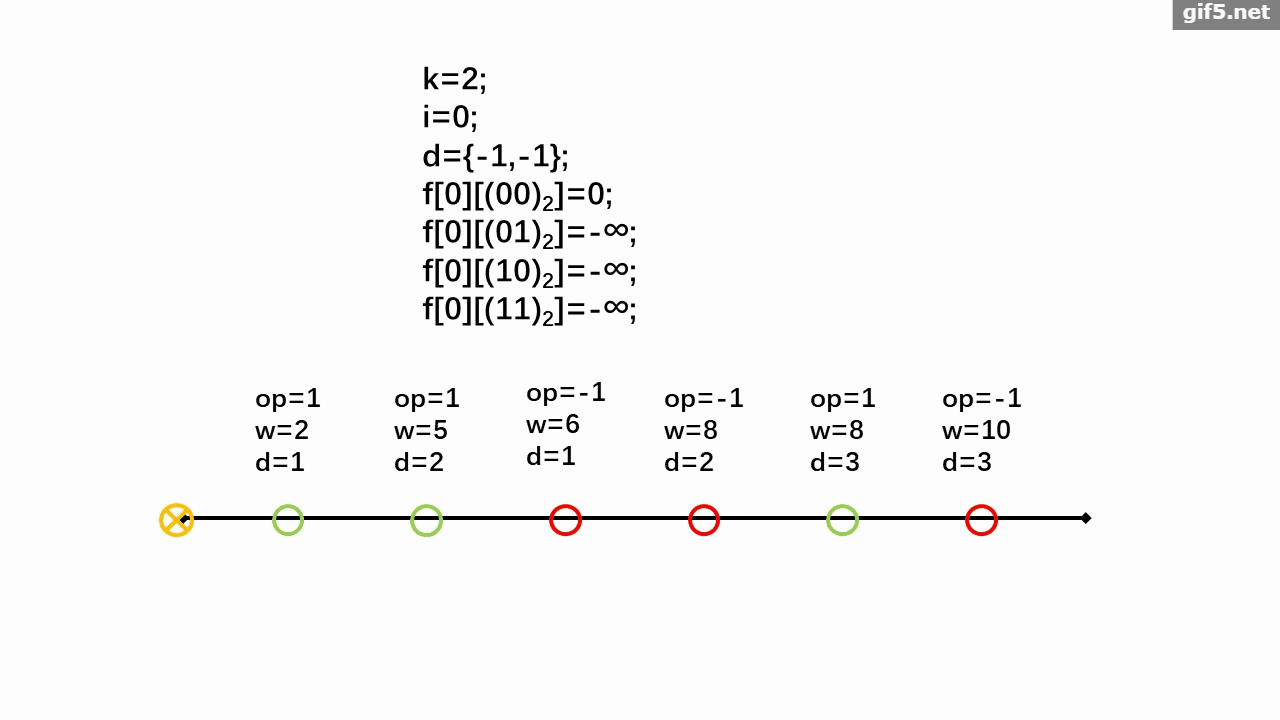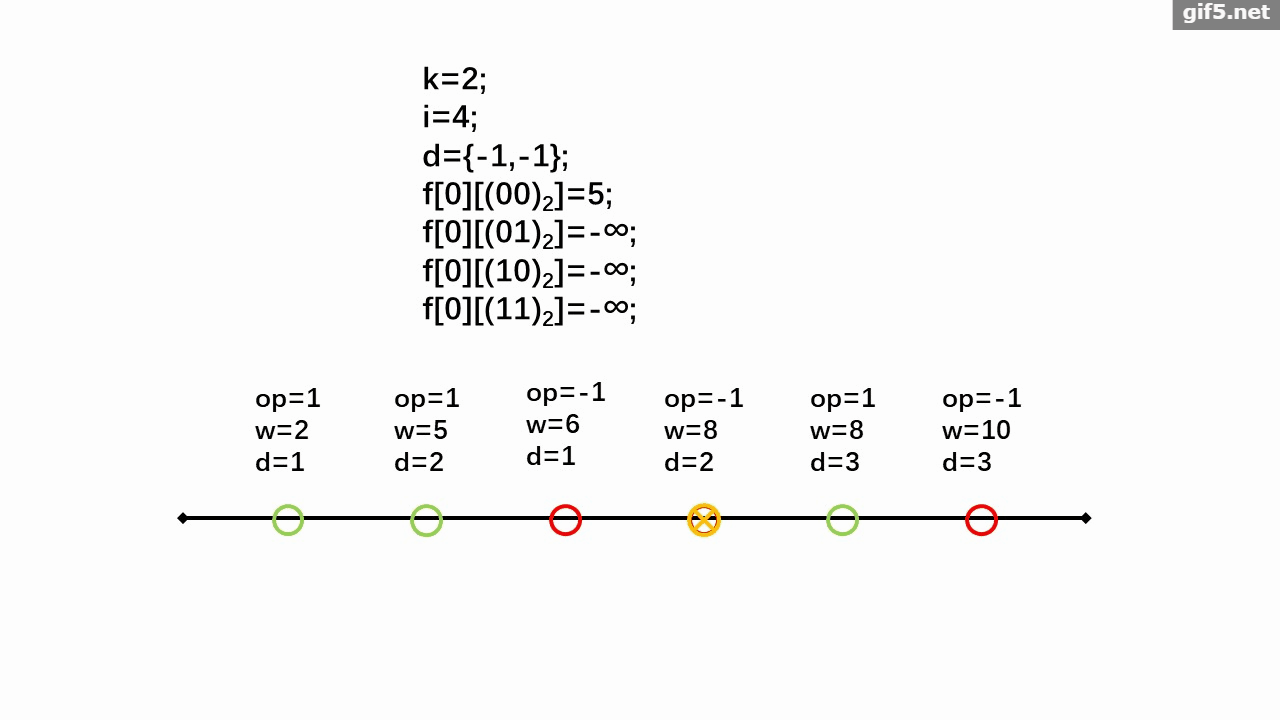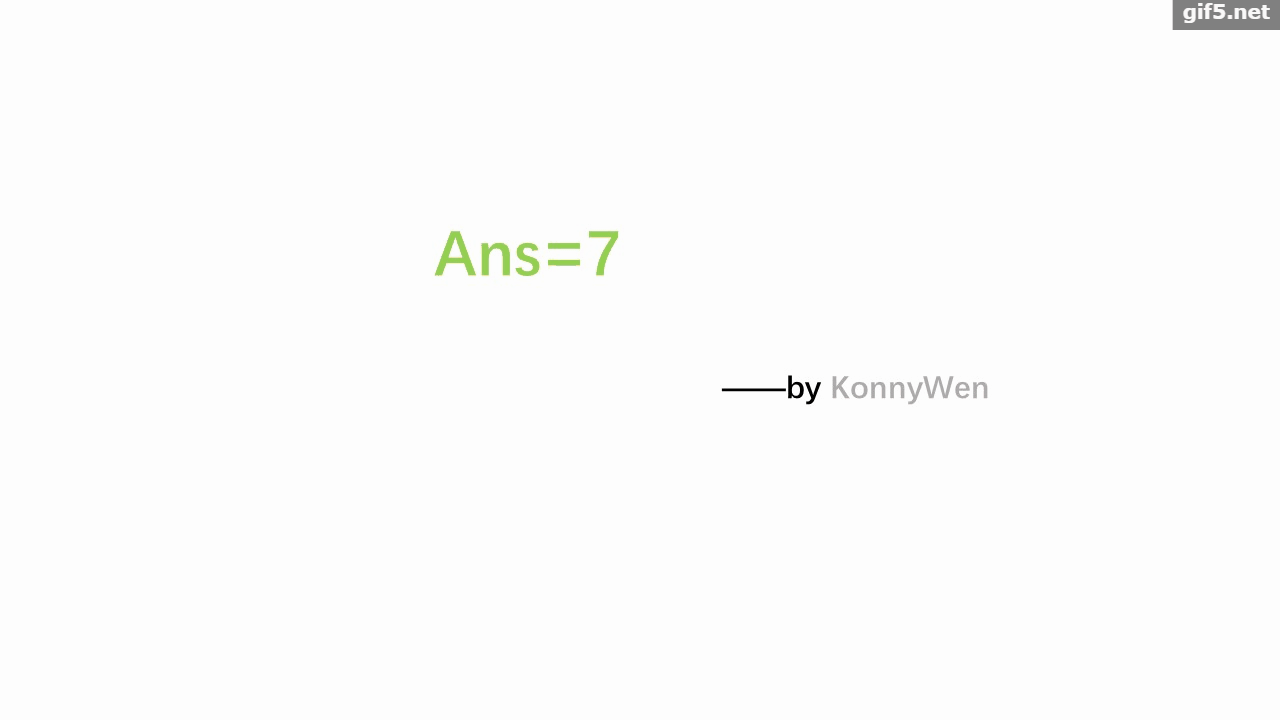
给定 $n$，$m$ 和 $k$。有一个序列 $a\{m\}$ 初始值为 $0$。有 $n$ 种操作，每种可以使 $[L_i,R_i]$ 区间序列值 $+1$。每个操作最多用 $1$ 次（可以不用）。保证对于每个 $i(1\le i\le n)$ 最多存在 $k$ 个不同的 $j$ 满足 $i\in[L_j,R_j]$。求最后的序列中奇数最多个数。
数据范围：$1\le n\le 10^5$，$1\le m\le 10^9$，$1\le k\le 8$。
阅读全文
给定 $n$，$m$ 和 $k$。有一个序列 $a\{m\}$ 初始值为 $0$。有 $n$ 种操作，每种可以使 $[L_i,R_i]$ 区间序列值 $+1$。每个操作最多用 $1$ 次（可以不用）。保证对于每个 $i(1\le i\le n)$ 最多存在 $k$ 个不同的 $j$ 满足 $i\in[L_j,R_j]$。求最后的序列中奇数最多个数。
数据范围：$1\le n\le 10^5$，$1\le m\le 10^9$，$1\le k\le 8$。
阅读全文
浙公网安备 33010602011771号