算法刷题 Day 27 | ● 39. 组合总和 ● 40.组合总和II ● 131.分割回文串

今日任务

• 组合总和
• 组合总和II
• 分割回文串

详细布置

39. 组合总和

本题是 集合里元素可以用无数次，那么和组合问题的差别 其实仅在于 startIndex上的控制

题目链接/文章讲解：https://programmercarl.com/0039.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C.html

视频讲解：https://www.bilibili.com/video/BV1KT4y1M7HJ

Tips：本题只需要控制pos不要+1即可

我的题解：

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    int sum = 0;
    void backtracking(vector<int>&candidates, int target,int pos){
        if(sum == target){
            result.push_back(path);
            return;
        }
        else if(sum > target){
            return;
        }

        for(int i = pos; i<candidates.size(); i++){
            sum+=candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates,target,i);
            path.pop_back();
            sum-=candidates[i];
        }
    }   
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtracking(candidates,target,0);
        return result;
    }
};

40.组合总和II

本题开始涉及到一个问题了：去重。

注意题目中给我们 集合是有重复元素的，那么求出来的 组合有可能重复，但题目要求不能有重复组合。

题目链接/文章讲解：https://programmercarl.com/0040.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8CII.html

视频讲解：https://www.bilibili.com/video/BV12V4y1V73A

Tips：为了去重，要先对数组进行排序，并新建一个flag数组用于记录是否访问过之前数值相同的元素。

前面我们提到：要去重的是“同一树层上的使用过”，如何判断同一树层上元素（相同的元素）是否使用过了呢。

如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。

此时for循环里就应该做continue的操作。

这块比较抽象，如图：

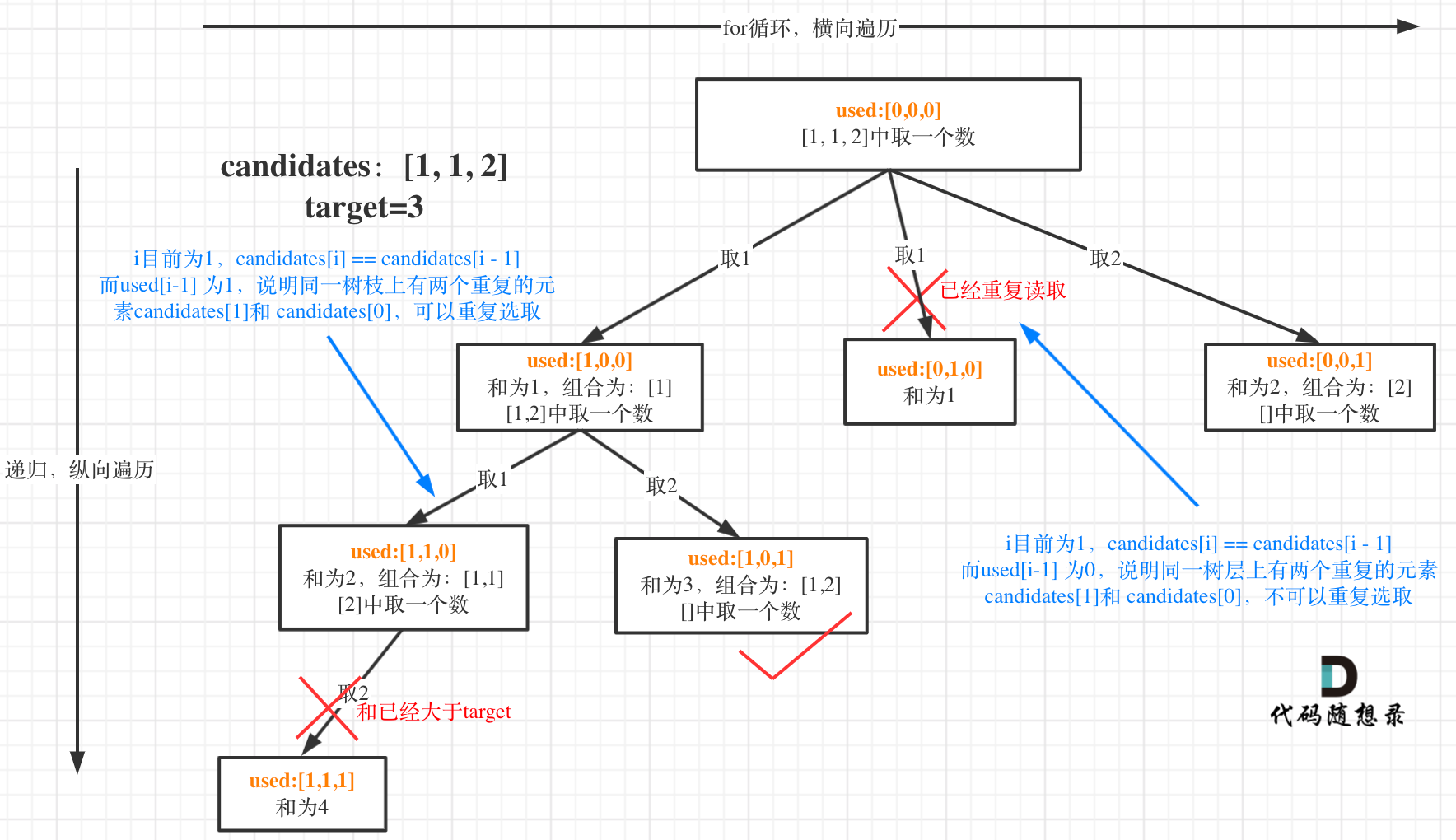
我在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：

• used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
• used[i - 1] == false，说明同一树层candidates[i - 1]使用过

可能有的录友想，为什么 used[i - 1] == false 就是同一树层呢，因为同一树层，used[i - 1] == false 才能表示，当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。

而 used[i - 1] == true，说明是进入下一层递归，去下一个数，所以是树枝上，如图所示：

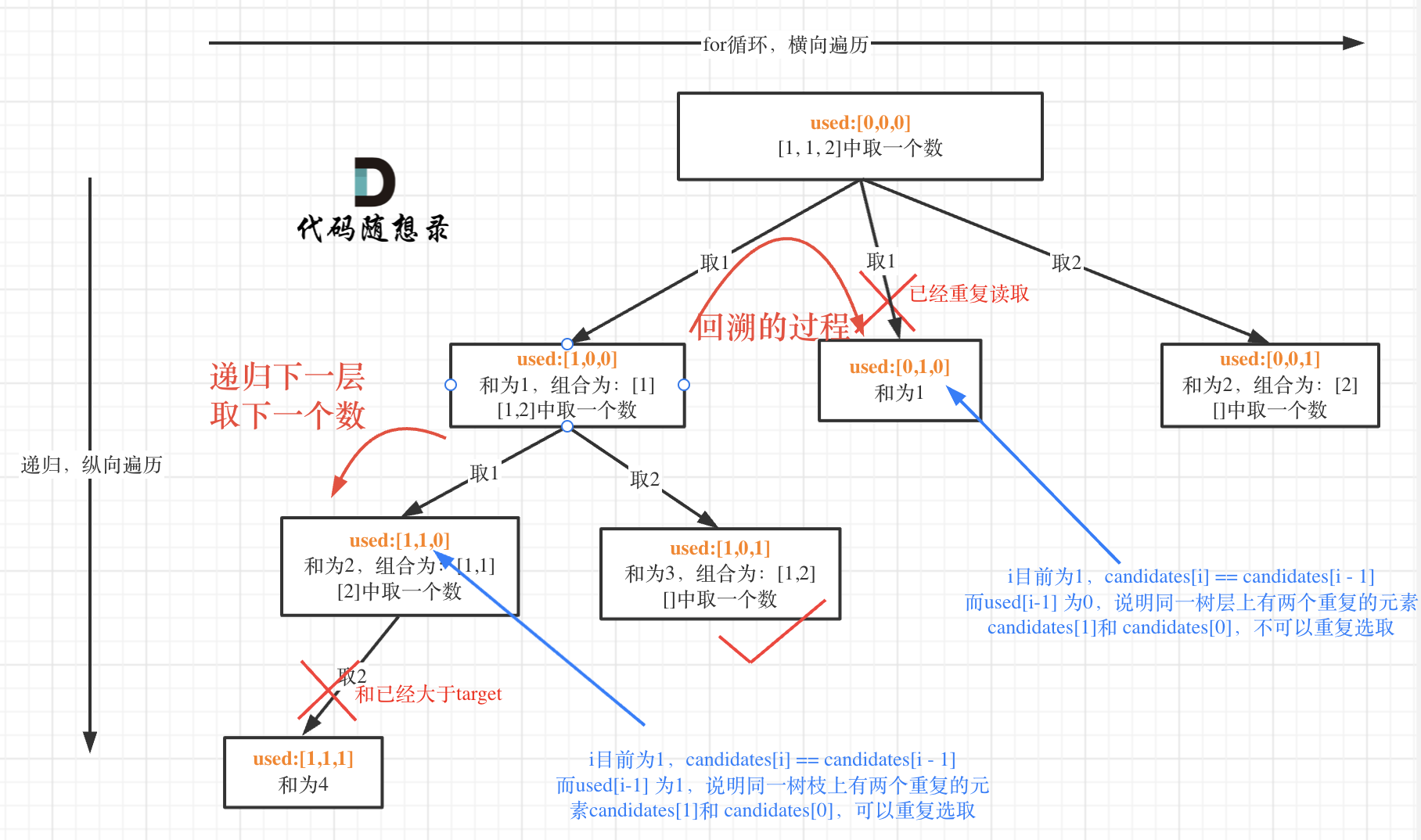
我的题解：

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    int sum = 0;

    void backtracking(vector<int>& candidates, int target, int pos, vector<bool>& flag){
        if(sum == target){
            result.push_back(path);
            return;
        }
        if(sum > target){
            return;
        }

        for(int i = pos;i<candidates.size();i++){
            if(i > 0 && candidates[i] == candidates[i-1] && flag[i-1] == false){
                continue;
            }
            sum+=candidates[i];
            path.push_back(candidates[i]);
            flag[i] = true;
            backtracking(candidates,target,i+1,flag);
            flag[i] = false;
            path.pop_back();
            sum-=candidates[i];
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> flag(candidates.size(),false);
        sort(candidates.begin(),candidates.end());
        backtracking(candidates,target,0,flag);
        return result;
    }
};

131.分割回文串

本题较难，大家先看视频来理解 分割问题，明天还会有一道分割问题，先打打基础。

https://programmercarl.com/0131.%E5%88%86%E5%89%B2%E5%9B%9E%E6%96%87%E4%B8%B2.html

视频讲解：https://www.bilibili.com/video/BV1c54y1e7k6

Tips：其实就是把组合问题倒过来想，但是要注意，在回溯过程中进入下一层是应该用 i + 1 而不是startpos + 1

我的题解：

class Solution {
public:
    vector<vector<string>> result;
    vector<string> path;

    void backtracking(string s, int startPos){
        if(startPos >= s.size()){
            result.push_back(path);
            return;
        }

        for(int i = startPos; i<s.size();i++){
            string front = s.substr(startPos,i - startPos + 1);
            if(judge(front)){
                path.push_back(front);
                //注意这里应该是i+1,而不是startpos+1
                backtracking(s,i+1);
                path.pop_back();
            }
        }
    }

    bool judge(string str){
        int i = 0;
        int j = str.size() - 1;
        while(i <= j){
            if(str[i]!=str[j]){
                return false;
            }
            i++;
            j--;
        }
        return true;
    }

    vector<vector<string>> partition(string s) {
        backtracking(s,0);
        return result;
    }
};