算法刷题 Day 22 | 235. 二叉搜索树的最近公共祖先 701.二叉搜索树中的插入操作 450.删除二叉搜索树中的节点

今日内容：

• 二叉搜索树的最近公共祖先
• 二叉搜索树中的插入操作
• 删除二叉搜索树中的节点

详细布置

235. 二叉搜索树的最近公共祖先

相对于 二叉树的最近公共祖先 本题就简单一些了，因为 可以利用二叉搜索树的特性。

题目链接/文章讲解：https://programmercarl.com/0235.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B1%E7%A5%96%E5%85%88.html

视频讲解：https://www.bilibili.com/video/BV1Zt4y1F7ww

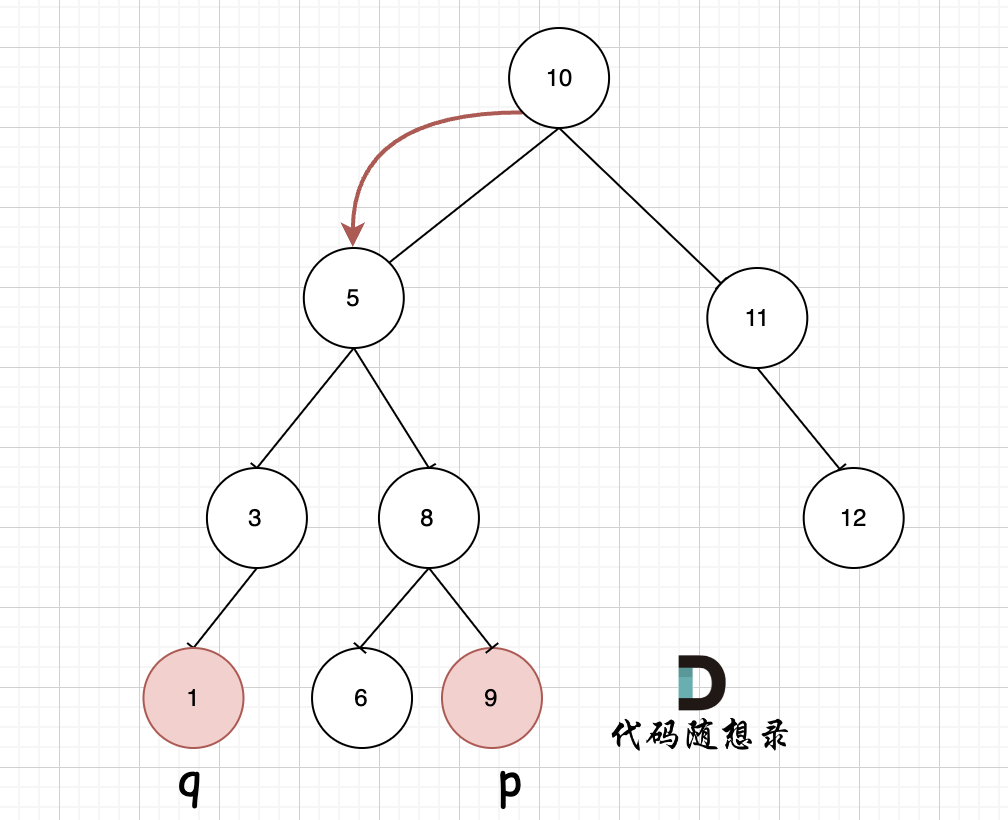
Tips：当我们从上向下去递归遍历，第一次遇到 cur节点是数值在[p, q]区间中，那么cur就是 p和q的最近公共祖先。

我的题解：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL){
            return NULL;
        }

        if(root->val > p->val && root->val > q->val){
            TreeNode* left = lowestCommonAncestor(root->left, p, q);
            if(left){
                return left;
            }
        }

        if(root->val < p->val && root->val < q->val){
            TreeNode* right = lowestCommonAncestor(root->right, p, q);
            if(right){
                return right;
            }
        }
        //剩下的情况，就是cur节点在区间
        //（p->val <= cur->val && cur->val <= q->val）或者 
        //（q->val <= cur->val && cur->val <= p->val）中，
        // 那么cur就是最近公共祖先了，直接返回cur。
        return root;

    }
};

701.二叉搜索树中的插入操作

本题比想象中的简单，大家可以先自己想一想应该怎么做，然后看视频讲解，就发现 本题为什么比较简单了。

题目链接/文章讲解：https://programmercarl.com/0701.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E6%8F%92%E5%85%A5%E6%93%8D%E4%BD%9C.html

视频讲解：https://www.bilibili.com/video/BV1Et4y1c78Y

Tips：

这道题目其实是一道简单题目，但是题目中的提示：有多种有效的插入方式，还可以重构二叉搜索树，一下子吓退了不少人，瞬间感觉题目复杂了很多。

其实可以不考虑题目中提示所说的改变树的结构的插入方式。只要按照二叉搜索树的规则去遍历，遇到空节点就插入节点就可以了。

本题通过递归函数返回值完成新加入节点的父子关系赋值操作，下一层将加入节点返回，本层用root->left或者root->right将其接住。

我的题解：

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root == NULL){
            TreeNode* node = new TreeNode(val);
            return node;
        }

        if(val > root->val){
            root->right = insertIntoBST(root->right, val);
        }
        else{
            root->left = insertIntoBST(root->left, val);
        }
        return root;
    }
};

450.删除二叉搜索树中的节点

相对于 插入操作，本题就有难度了，涉及到改树的结构

题目链接/文章讲解：https://programmercarl.com/0450.%E5%88%A0%E9%99%A4%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B9.html

视频讲解：https://www.bilibili.com/video/BV1tP41177us

Tips：

递归三部曲：

• 确定递归函数参数以及返回值

说到递归函数的返回值，在二叉树：搜索树中的插入操作 (opens new window)中通过递归返回值来加入新节点， 这里也可以通过递归返回值删除节点。

代码如下：

TreeNode* deleteNode(TreeNode* root, int key)

• 确定终止条件

遇到空返回，其实这也说明没找到删除的节点，遍历到空节点直接返回了

if (root == nullptr) return root;

• 确定单层递归的逻辑

这里就把二叉搜索树中删除节点遇到的情况都搞清楚。

有以下五种情况：

• 第一种情况：没找到删除的节点，遍历到空节点直接返回了
• 找到删除的节点
  • 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
  • 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
  • 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
  • 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

第五种情况有点难以理解，看下面动画：

动画中的二叉搜索树中，删除元素7， 那么删除节点（元素7）的左孩子就是5，删除节点（元素7）的右子树的最左面节点是元素8。

将删除节点（元素7）的左孩子放到删除节点（元素7）的右子树的最左面节点（元素8）的左孩子上，就是把5为根节点的子树移到了8的左孩子的位置。

要删除的节点（元素7）的右孩子（元素9）为新的根节点。

我的题解：

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root == NULL){
            return NULL;
        }
        if(root->val == key){
            if(root->left == NULL && root->right == NULL){
                return NULL;
            }
            else if(root->left == NULL && root->right!=NULL){
                return root->right;
            }
            else if(root->left != NULL && root->right == NULL){
                return root->left;
            }
            else{
                TreeNode* cur = root->right;
                while(cur->left!=NULL){
                    cur = cur->left;
                }
                cur->left = root->left;
                return root->right;
            }            
        }
        
        // 这里相当于把新的节点返回给上一层，上一层就要用 root->left 或者 root->right接住，代码如下：
        if(root->val > key){
            root->left = deleteNode(root->left,key);
        }
        else{
            root->right = deleteNode(root->right,key);
        }
        return root;

    }
};