202507 贪心杂题(模拟费用流)笔记
一、模拟费用流
有的贪心可以用费用流建模解决,但是直接跑费用流会 T 飞,分析增广路的形式,可以用其它方式表示并快速解决。
じゃ、始めます。
1. CF865D Buy Low Sell High
建出如下费用流模型,跑最大费用流,逗号前是流量限制,逗号后是费用。
第一种增广路如下,就是在当前 \(a_i\) 往前找一个最小的 \(-a_j\) 配对,费用是 \(-a_j+a_i\)。
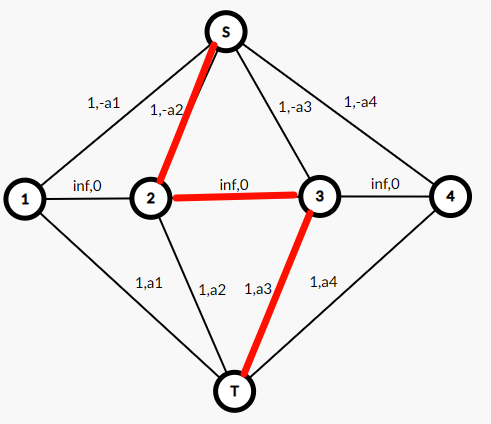
第二种增广路如下(红色)。
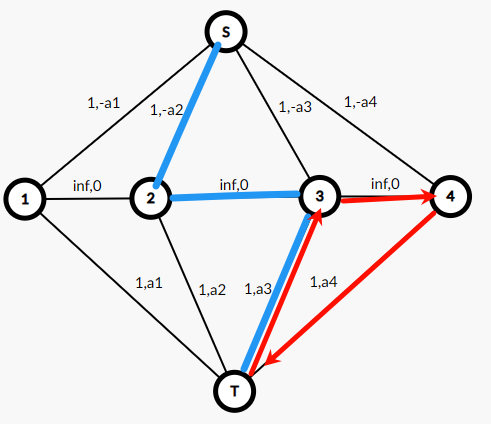
其等价于 Day 3 不卖,留到 Day 4 卖,原因是 \(-a_3+a_4\ge 0\)。
上述两种增广路使用优先队列维护即可,这就是反悔贪心。
点击查看代码
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> x;
q.push(-x);
if (x + q.top() >= 0) {
ans += x + q.top();
q.pop();
q.push(-x);
}
}
cout << ans;
2. CF730I Olympiad in Programming and Sports
先贪心地给 \(a\) 队全选最大,那么接下来一队要么就选 \(b\) 前几大的;要么就已经选了的 \(a\) 吐一个出来选 \(b\),再选一个 \(a\),表示成费用流如红色所示(每个点连汇点 \(T\) 其实都有两条 \(a,b\),这个画图软件画不出来)。
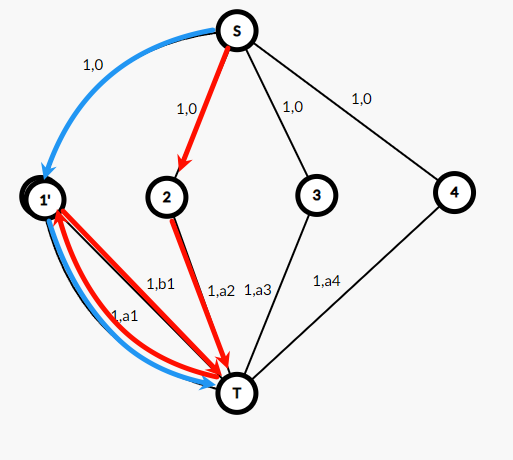
也是整个堆就好了。
点击查看代码
cin >> n >> p >> s;
for (int i = 1; i <= n; i++) {
cin >> a[i];
qa.push({a[i], i});
}
while (p--) {
auto [x, i] = qa.top();
qa.pop();
ans += x;
visa[i] = true;
}
for (int i = 1; i <= n; i++) {
cin >> b[i];
if (visa[i])
qab.push({b[i] - a[i], i});
else
qb.push({b[i], i});
}
while (s--) {
while (!qa.empty() and (visa[qa.top().second] or visb[qa.top().second]))
qa.pop();
while (!qb.empty() and (visa[qb.top().second] or visb[qb.top().second]))
qb.pop();
if (qa.empty()) {
ans += qb.top().first;
visb[qb.top().second] = true;
qb.pop();
continue;
}
auto [xa, ia] = qa.top();
auto [xb, ib] = qb.top();
auto [xab, iab] = qab.top();
int s = xab + xa;
if (s > xb) {
ans += s;
visa[iab] = false;
visb[iab] = true;
visa[ia] = true;
qa.pop(), qab.pop();
qab.push({b[ia] - a[ia], ia});
} else {
ans += xb;
visb[ib] = true;
qb.pop();
}
}
cout << ans << "\n";
3. P4694 [PA 2013] Raper
费用流的费用随着流量增长而有凸性,假如当前流量越多花的钱反而比之前还少,那么显然可以交换现在和之前。对于这个限制汇点流量的问题,可以想到 WQS 二分。
WQS 加权费用后,求最小费用就会导致有的光盘绝对不优从而不造,转换成了上面类似的问题。
下图图源 YYC。
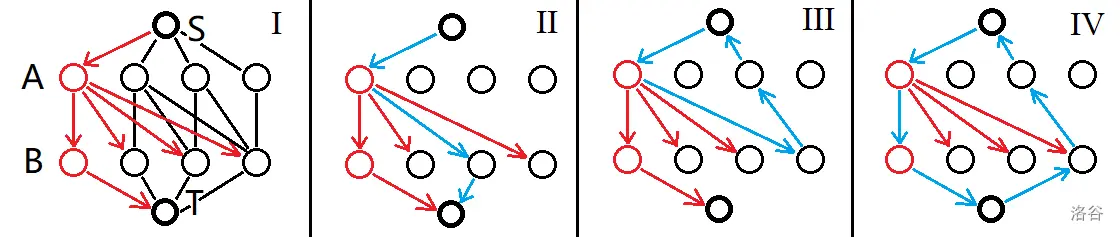
- I. 枚举到当前红色的工厂。
- II. 一种普通的增广路,光盘个数增加。
- III. 一种退流的增广路,相当于不用第三个 \(A\) 厂改用第一个 \(A\) 厂,\(B\) 厂保持不变,这说明费用减小而光盘个数不变。
- IV. 另一种退流的增广路,相当于完全用新厂造光盘,光盘个数不变,可是明显被退掉的旧厂在当前 WQS 加权下是优的,否则不会被选取,这种情况不合法。
所以只有 II,III 两种情况,和上面是一样的,用堆做即可。
4. P3826 [NOI2017] 蔬菜
去掉一些蔬菜的操作不好处理,那么就从最后一天时光倒流,不断地添加蔬菜。
费用流建模,其实同 T3,只是每过一天有的边的流量上限会增加。
那么实现就是堆里只放蔬菜类型不放蔬菜个数,每次把最贵的蔬菜拎出来卖,卖完了就看看能不能补货,不能直接扔了,特殊处理一下第一次卖的加权。
处理出如果只卖 \(x\) 个蔬菜,可以卖出的蔬菜个数 \(ans_x\),离线回答问题即可。
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define pii pair<int, int>
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
const int N = 1e6 + 10;
int n, m, k, tmx, A[N], S[N], C[N], X[N], t[N];
int st[N], top;
int sell[N], ans[N], na;
vector<int> vec[N];
bool cmp(int x, int y) {
return x > y;
}
signed main() {
IOS;
cin >> n >> m >> k;
for (int i = 1; i <= n; i++)
cin >> A[i] >> S[i] >> C[i] >> X[i];
for (int i = 1; i <= k; i++) {
cin >> t[i];
tmx = max(tmx, t[i]);
}
for (int i = 1; i <= n; i++)
if (!X[i])
vec[tmx].push_back(i);
else
vec[min(tmx, (C[i] + X[i] - 1) / X[i])].push_back(i);
priority_queue<pii> q;
for (int i = tmx; i; i--) {
for (int j : vec[i])
st[++top] = j;
for (int j = 1; j <= top; j++)
q.push({sell[st[j]] ? A[st[j]] : A[st[j]] + S[st[j]], st[j]});
top = 0;
for (int j = 1; j <= m and !q.empty();) {
auto [v, x] = q.top();
if (!sell[x]) {
sell[x] = 1;
q.pop();
j++;
if (C[x] - X[x] * (i - 1) - sell[x] > 0)
q.push({A[x], x});
else if (X[x])
st[++top] = x;
} else {
int c = min(C[x] - X[x] * (i - 1) - sell[x], m - j + 1);
sell[x] += c;
j += c;
if (C[x] - X[x] * (i - 1) - sell[x] == 0) {
q.pop();
if (X[x])
st[++top] = x;
}
}
}
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= sell[i]; j++) {
ans[++na] = A[i];
if (j == 1)
ans[na] += S[i];
}
sort(ans + 1, ans + na + 1, cmp);
for (int i = 1; i <= na; i++)
ans[i] += ans[i - 1];
for (int i = 1; i <= k; i++)
cout << ans[min(na, t[i] * m)] << "\n";
return 0;
}
5. P5470 [NOI2019] 序列
费用流建模方式也同 T3,而对于相同个数的限制,转换为不同个数的限制,让不同的必须经过一条流量上限为 \(m-k\) 的特殊边即可。
那么就有如下的五种情况:
- 直接选一对相同的。
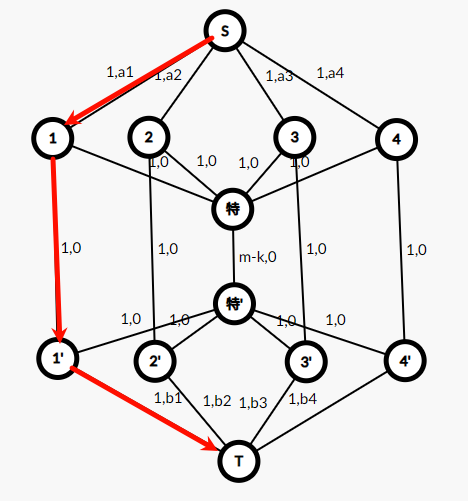
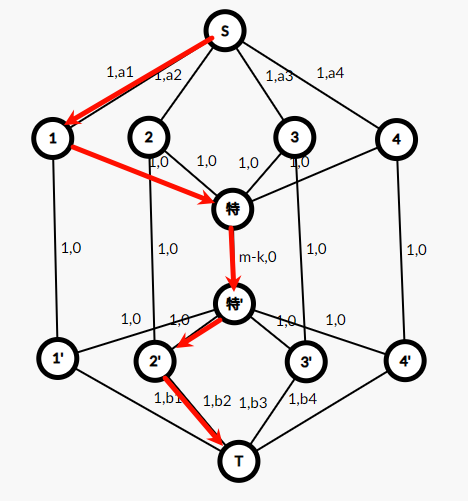
- 选一对不同的,且 \(a,b\) 均未被选的,特殊边流量增加。
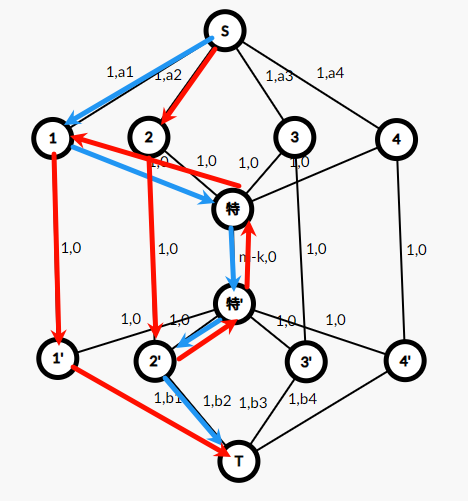
- 选一对不同的 \(a_i,b_j\),且 \(a_j,b_i\) 已经被选,如红色,特殊边流量减少
-
选一对不同的 \(a_i,b_j\),且 \(a_j\) 未被选,\(b_i\) 已被选。
-
选一对不同的 \(a_i,b_j\),且 \(b_i\) 未被选,\(a_j\) 已被选,如红色。
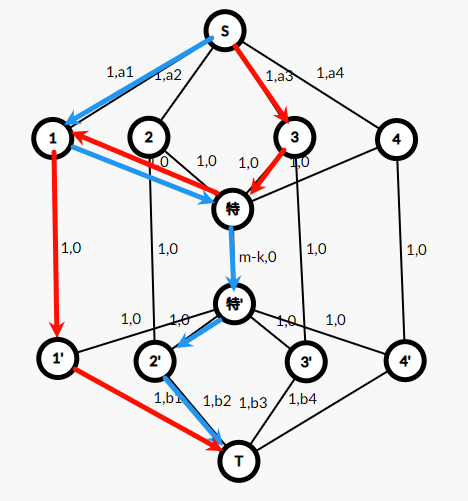
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define pii pair<int, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e5 + 10;
int T, n, k, l, a[N], b[N], ans;
bool visa[N], visb[N];
void clear() {
memset(visa, 0, sizeof visa);
memset(visb, 0, sizeof visb);
ans = 0;
}
void solve() {
clear();
cin >> n >> k >> l;
l = k - l;
priority_queue<pii> qs, qa, qb, qa2, qb2;
for (int i = 1; i <= n; i++) {
cin >> a[i];
qa.push({a[i], i});
}
for (int i = 1; i <= n; i++) {
cin >> b[i];
qb.push({b[i], i});
qs.push({a[i] + b[i], i});
}
while (k--) {
while (!qs.empty() and (visa[qs.top().se] or visb[qs.top().se]))
qs.pop();
while (!qa.empty() and (visa[qa.top().se] or visb[qa.top().se]))
qa.pop();
while (!qb.empty() and (visa[qb.top().se] or visb[qb.top().se]))
qb.pop();
while (!qa2.empty() and visa[qa2.top().se])
qa2.pop();
while (!qb2.empty() and visb[qb2.top().se])
qb2.pop();
int chs = 0, ret = 0;
if (!qs.empty() and ret < qs.top().fi) {
ret = qs.top().fi;
chs = 1;
}
if (!qa.empty() and !qb.empty() and qa.top().se != qb.top().se and ret < qa.top().fi + qb.top().fi and l) {
ret = qa.top().fi + qb.top().fi;
chs = 2;
}
if (!qa2.empty() and !qb2.empty() and ret < qa2.top().fi + qb2.top().fi) {
ret = qa2.top().fi + qb2.top().fi;
chs = 3;
}
if (!qa2.empty() and !qb.empty() and ret < qa2.top().fi + qb.top().fi) {
ret = qa2.top().fi + qb.top().fi;
chs = 4;
}
if (!qa.empty() and !qb2.empty() and ret < qa.top().fi + qb2.top().fi) {
ret = qa.top().fi + qb2.top().fi;
chs = 5;
}
ans += ret;
if (chs == 1) {
auto [v, i] = qs.top();
qs.pop();
visa[i] = visb[i] = true;
}
if (chs == 2) {
auto [va, ia] = qa.top();
auto [vb, ib] = qb.top();
qa.pop(), qb.pop();
visa[ia] = visb[ib] = true;
qa2.push({a[ib], ib});
qb2.push({b[ia], ia});
l--;
}
if (chs == 3) {
auto [va2, ia2] = qa2.top();
auto [vb2, ib2] = qb2.top();
qa2.pop(), qb2.pop();
visa[ia2] = visb[ib2] = true;
l++;
}
if (chs == 4) {
auto [va2, ia2] = qa2.top();
auto [vb, ib] = qb.top();
qa2.pop(), qb.pop();
visa[ia2] = visb[ib] = true;
qa2.push({a[ib], ib});
}
if (chs == 5) {
auto [va, ia] = qa.top();
auto [vb2, ib2] = qb2.top();
qa.pop(), qb2.pop();
visa[ia] = visb[ib2] = true;
qb2.push({b[ia], ia});
}
}
cout << ans << "\n";
}
signed main() {
IOS;
cin >> T;
while (T--)
solve();
return 0;
}
6. CF2029I Variance Challenge
答案要求的东西等价于
\(nx\) 就是序列的和,记作 \(s\)。
显然,修改序列后 \(s'\) 的结果不会超过 \(nm\) 个,且 \(k\mid(s'-s)\),直接枚举 \(s'\)。
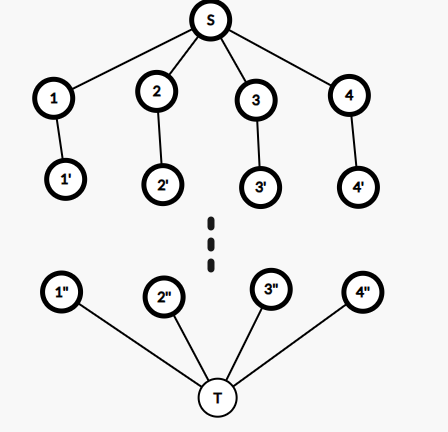
建出如图所示的费用流,一次操作就相当于操作一些竖边的流量,这就是一个最小子段和,正流和退流都做一次即可。
费用就是修改前后,对所求式子影响的差值,可以 \(O(1)\) 计算。
点击查看代码
cin >> n >> m >> k;
int ave = 0;
for (int i = 1; i <= n; i++) {
cin >> a[i];
ave += a[i];
}
for (int i = 1; i <= m; i++)
ans[i] = oo;
for (int av = ave; av <= ave + n * m * k; av += k) {
i128 RET = 0;
for (int i = 1; i <= n; i++) {
ps[i] = pw((a[i] + k) * n - av) - pw(a[i] * n - av);
ng[i] = oo;
cnt[i] = 0;
RET += pw(a[i] * n - av);
}
for (int i = 1; i <= m; i++) {
i128 s = 0, mx = 0, ret = 0;
int l, r, mxp = 0, op = 0;
for (int j = 1; j <= n; j++) {
s += ps[j];
if (ret > s - mx) {
ret = (j == 1 ? s : s - mx);
l = mxp + 1, r = j;
op = 1;
}
if (mx < s) {
mx = s;
mxp = j;
}
}
s = 0, mx = 0, mxp = n + 1;
for (int j = n; j; j--) {
s += ng[j];
if ((j == n and ret > s) or (j != n and ret > s - mx)) {
ret = (j == n ? s : s - mx);
l = j, r = mxp - 1;
op = 2;
}
if (mx < s) {
mx = s;
mxp = j;
}
}
RET += ret;
ans[i] = min(ans[i], RET);
if (op == 1) {
for (int j = l; j <= r; j++) {
cnt[j]++;
ng[j] = pw((a[j] + (cnt[j] - 1) * k) * n - av) - pw((a[j] + cnt[j] * k) * n - av);
ps[j] = pw((a[j] + (cnt[j] + 1) * k) * n - av) - pw((a[j] + cnt[j] * k) * n - av);
}
} else if (op == 2) {
for (int j = l; j <= r; j++) {
cnt[j]--;
ps[j] = pw((a[j] + (cnt[j] + 1) * k) * n - av) - pw((a[j] + cnt[j] * k) * n - av);
if (!cnt[j])
ng[j] = oo;
else
ng[j] = pw((a[j] + (cnt[j] - 1) * k) * n - av) - pw((a[j] + cnt[j] * k) * n - av);
}
}
}
}
for (int i = 1; i <= m; i++)
write(ans[i] / n), cout << " ";
cout << "\n";
二、Exchange Argument
1. AT_agc023_f [AGC023F] 01 on Tree
假设某个节点点权为 \(0\),那么选完它的父亲就要立即选它,所以可以把它和它的父亲“绑定”。
假如某个节点的儿子 \(A\) 中有 \(a_0\) 个 \(0\) 和 \(a_1\) 个 \(1\),儿子 \(B\) 中有 \(b_0\) 个 \(0\) 和 \(b_1\) 个 \(1\),先绑定 \(A\) 的条件是 \(a_1b_0\le a_0b_1\),移项得
小根堆贪心做即可。
三、杂题
1. P7417 [USACO21FEB] Minimizing Edges P
容易观察到 \(f\) 取决于最小的同奇偶最短路,因为假如 \(f(a,b)\) 可以,那么反复横跳 \(k\) 步,\(f(a,b+2k)\) 也可以。
求出原图的奇偶最短路,没有边权 BFS 即可。
假如一个点同时有奇最短路和偶最短路,那么所有点显然都有两种最短路。
因此,当 \(1\) 号点没有偶最短路时,奇偶最短路构成一棵树,答案为 \(n-1\)。
当 \(1\) 号点的奇偶最短路是 \((0,1)\) 时,只需要在树上 \(1\) 点加一个自环,答案为 \(n\)。
假设一个点的奇数最短路和偶数最短路组成一个二元组 \((x,y)\)(其中 \(x<y\)),那么为了得到 \((x,y)\),可以:
- 向 \((x-1,y-1)\) 代表的点连边。
- 向 \((x-1,y+1)\),\((x+1,y-1)\) 代表的点连边。
- 当 \(x+1=y\) 时,\(c\) 个剩余的 \((x,y)\) 间两两配对连 \(\left\lceil\frac{c}{2}\right\rceil\) 条边。
分析一下这个连边,两两恰好配对肯定最优,若不能恰好配对才考虑很多个点搭到一个点上。
实现的时候,按 \(x+y\) 从小到大为第一维(越大称之为“下”),\(x\) 从小到大为第二维操作(越大称之为“右”)。
对于第一种情况,如果一个点有上面的点,那肯定是往上连最好,因为第一种情况只需花费一条边。
但通常,左边可能有 \(x\) 个点不得不往右连,那么分 \(x\) 个点给左边显然更优,原因就是上面的“分析”。
分了 \(x\) 个点后,当前的剩下点就直接往上或往右连,可以知道往右连的一定是分出去的 \(x\) 个点,加上这部分往右连的贡献,并统计这个点要向右边拿多少点。
最后特判情况三。
点击查看代码
// vec:排序后点集
// mp:(x, y) 点个数
// lf:(x, y) 要向右边要多少个点
for (auto [x, y] : vec) {
if (!x)
continue;
int nw = mp[x][y];
int up = mp[x - 1][y - 1];
int l = lf[x - 1][y + 1];
ans += max(0ll, nw - l); // 分出去 l 个点,剩下的点向上或向右
if (up)
nw = min(nw, l);
// 如果有上面的点,那么 nw - l 可以向上连,可能只有 l 个点要向右
// 否则所有点都只能向右
ans += (x + 1 != y ? lf[x][y] = nw : (nw + 1) / 2);
}
2. CF1566F Points Movement
初始被点覆盖的区间不用管,包含了小区间的大区间不用管,因为为了删掉小区间,一定会先把大区间删了。
设 \(f_{i,0/1}\) 表示考虑到第 \(i\) 个点,第 \(i\) 个点向左 / 右走,消完 \(i\) 点左侧 所有区间的最小价值。
那么枚举 \(i\) 点和 \(i-1\) 点之间的区间,肯定是 \(i\) 点到一个,\(i-1\) 点到相邻的另一个,那么就有转移方程
其中 \(L=l_{j-1}-a_{i-1},R=a_i-r_j\)。
注意处理边界,DP 线性,瓶颈在对区间的预处理,复杂度 \(O(n+m+m\log m)\)。
3. CF1592F1 Alice and Recoloring 1
第二,三种操作一定不优,因为两次一操作就能达成同样的效果。
第四种操作只有在操作一次时最优,如果操作两次第四种操作,显然可以被这样替代
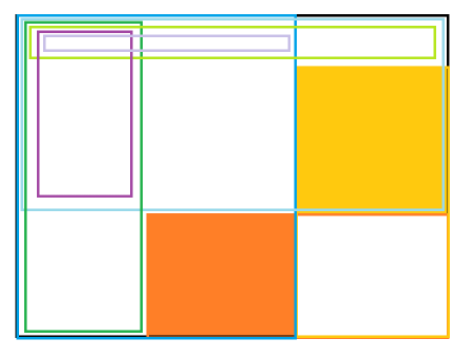
橙+黄要 \(6'\),其他所有一操作加起来也恰好是 \(6\) 次。
因此第一种比第四种优的只有这种情况,即存在一个右下角的矩形它的四角都要一操作:
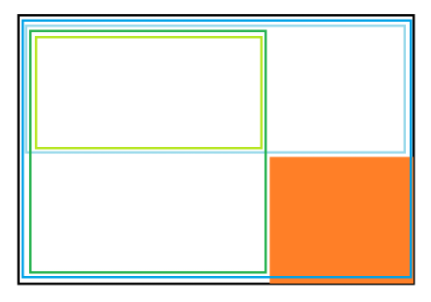
当只有操作一的时候,可以从右下角往左上角差分,即 \(s_{i,j}=a_{i,j}\oplus a_{i+1,j}\oplus a_{i,j+1} \oplus a_{i+1,j+1}\),可以发现,一次操作一就是改变 \(s\) 中的一个数,\(a\) 全白就是 \(s\) 全为 \(1\)(令黑色是 \(1\))。
数一下并找是否存在操作四即可,时间复杂度 \(O(nm)\)。
4. CF1592F2 Alice and Recoloring 2
此时操作四更优,观察发现,对于所有进行了操作四的 \((x,y)\to (n,m)\) 矩形,每个 \(x\) 只会出现一次,每个 \(y\) 只会出现一次。
假设有一个 \(x\) 出现了两次:

被操作一替代了。
这个问题就变成了经典的二分图匹配问题。
5. CF1753E N Machines
首先,乘法一定丢最后,加法一定丢最前面,这样能够贡献更大。
其次,初始答案不超过 \(2\times 10^9\),排除掉无用的 \(\times 1\) 操作,至多只会有 \(30\) 个乘法操作。并且最劣情况下,答案最多变为平方,不会超过 long long 范围。
考虑 \(a_i\) 相同的乘法,\(i\) 小的显然后移后能够惠及更多加法,更加优,故以此为剪枝状态对选择哪些乘法进行爆搜,据说状态数很少,不超过 \(2^{11}\)。
确定了乘法操作后,如何确定加法呢?两个乘法操作之间的加法操作,受到的“倍率”是相同的,故可以一起考虑。先二分出加法操作中最小的贡献值 \(x\),check 中对每段加法二分,数出最小贡献值达到 \(x\) 需要多少次加法操作。
二分贡献最小值的值域是 \(a^2\) 而不是 \(a\);二分时,有可能包含恰好等于 \(x\) 的贡献后,代价超出,也有可能去除恰好等于 \(x\) 的贡献后,代价有余。需要注意如何正确且完全利用代价,我的做法是做包含和去除的两次二分。
6. CF1446D1 Frequency Problem (Easy Version)
首先,如果整个序列不止一个众数,那么答案就是整个序列。
其次,答案区间的众数一定包含原区间的众数。假设答案区间的众数 \(x'\) 不包含原区间的众数 \(x\),那么在答案区间中,\(x'\) 的个数大于 \(x\) 的个数。不断拓展区间,最后整个序列中 \(x'\) 的个数小于 \(x\) 的个数,则必然存在某个时刻,\(x'\) 的个数等于 \(x\) 的个数,此时区间大于答案区间。
所以枚举哪一个数是答案区间的第二个众数,问题变为在序列中找一段区间,使两种数个数相等。
利用传奇题目鸡蛋的思想,将一种数设为 \(1\),另一种数设为 \(-1\),做前缀和,区间 \([i,j]\) 合法,说明 \(s_{i-1}=s_j\),由于 \(s\) 的取值只有 \(2n\) 种,直接记录每种取值最早的出现位置即可解决问题。
时间复杂度 \(O(na)\)。
7. CF1446D2 Frequency Problem (Hard Version)
值域扩大后,这种和值域相关的复杂度通常采用根号分治解决。
对于出现次数 \(\ge \sqrt n\) 的数,个数 \(<\sqrt n\) 个,直接采用上面的做法,时间复杂度 \(O(n\sqrt n)\)。
对于出现次数 \(<\sqrt n\) 的数,直接枚举答案区间众数的出现次数 \(t\),接着双指针扫一遍区间,限制答案区间内数的出现次数不超过 \(t\),当出现次数为 \(t\) 的数超过 \(2\) 个时,\([l,r]\) 就是一个合法的答案。
维护区间内个数,和个数的个数,只需要用莫队一样的方法解决即可,时间复杂度 \(O(n\sqrt n)\)。
8. AT_agc016_e [AGC016E] Poor Turkeys
原来火鸡也是鳥吗(虽说有鳥焼き是烧鸡这种词)。
删的不好做,直接时光倒流,设 \(f_{i,x}=0/1\) 表示为了保住 \(i\),是否要吃了 \(x\)。初始时 \(f_{i,i}\gets1\)。
如果倒流到有一次操作要吃 \((x,y)\),而 \(f_{i,x}=1\),那么为了保住 \(x\) 后面给保 \(i\) 用,必须吃掉 \(y\);为了有 \(y\) 吃,在此之前必须保住 \(y\),\(f_{i,y}\gets1\)。
如果出现了一次 \(x,y\) 都必须要保住,但是必须选一个吃,那 \(i\) 肯定死翘翘了。
如果两只鸟 \((i,j)\),都需要靠吃 \(k\) 来保住,那么 \((i,j)\) 总有一个得死,不能成为答案。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号