线性基 笔记

异或空间线性基，和向量空间线性基对于向量空间一样，异或空间线性基内的元素针对一个集合 \(A\)。对于 \(A\) 内任意的一种异或结果，线性基内都有且只有一种组合方式异或出这种结果。

一、基本操作

1. 插入

定义 \(a_i\) 为线性基，其中 \(a_i\) 里放的数最高位只能为第 \(i\) 位。

当插入一个 \(x\) 时，从高往低考虑，如果 \(a_i\) 没有数，放进去，否则令 \(x\) 异或 \(a_i\)，继续往下走。

首先，\(x\) 异或 \(a_i\) 去掉了最高位，其次 \(a_i\) 本身就表示了一些数的异或结果，\(x\) 异或上 \(a_i\) 就是异或上那些数，可以发现总能异或回来原本有的那些数。

2. 判断是否存在一个数 / 查询异或最大值

同理从高到低位找即可。

3. 查询异或最小值

可以证明，线性基中不存在异或出来为 \(0\)。假如 \(a_{i1}\oplus a_{i2}\oplus \dots \oplus a_j=0\)，则 \(\oplus_{p} a_{ip}=a_j,a_j=a_j\)，与线性基的唯一性冲突。

所以最小值就是线性基里的最小值。

4. 模板代码

P3812 【模板】线性基。

点击查看代码

void insert(int x) {
    for (int i = M; i >= 0; i--)
        if (x >> i & 1) {
            if (!a[i]) {
                a[i] = x;
                return;
            } else
                x ^= a[i];
        }
}
int query() {
    int ret = 0;
    for (int i = M; i >= 0; i--)
        ret = max(ret, ret ^ a[i]);
    return ret;
}

二、一些定理

定理 1

\[\mathsf{\text{线性基异或值个数为 }} 2^n\mathsf{\text{。}} \]

证明：由于不生成重复元素，那么就是选或不选问题。

三、刷题总结

类 1：图上路径问题类

(1). P4151 [WC2011] 最大XOR和路径

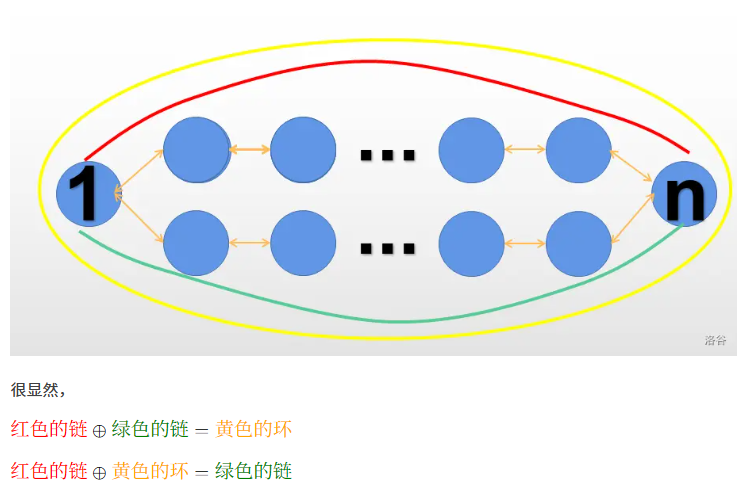
答案一定是一条 \(1\to n\) 的路径异或上若干个环，因为折返的路径都抵消掉了。

借用线性基的思想，两条 \(1\to n\) 路径异或出一个环，那么用所有的环去异或一条路径即可。

图源洛谷 @jun头吉吉：