后缀数组（SA） 笔记

过于困难了。

用于解决一个字符串 \(s\) 所有后缀的排名，一个后缀 \(s[i\dots n]\) 的编号定义为 \(i\)。

一、求 sa 数组

swap 前的数组意义：

• \(sa_i\)：排名为 \(i\)，长度为 \(k\) 的子串的编号。
• \(x_i\)：起点为 \(i\)，长度为 \(k\) 的子串的排名。
• \(y_i\)：第二关键字排名为 \(i\)，长度为 \(k\) 的子串的起点。

swap 后的数组意义：

• \(x_i\)：起点为 \(i\)，长度为 \(2k\) 的子串的排名。
• \(y_i\)：swap 前的 \(x_i\)。

算法流程是：先倍增枚举一个 \(k\)，每次只求出长度为 \(2k\) 的子串（即第一关键字和第二关键字长度都为 \(k\)）的三个数组，然后将后面的合并到前面。

预处理一个字符
s:  |  a  |  b  |  a  |  b  |  a  |
x:  | 97  | 98  | 97  | 98  | 97  |

sa: |  5  |  3  |  1  |  4  |  2  |

k = 1
s:   | a+b | b+a | a+b | b+a | a+_ |
oldx:|  1  |  2  |  1  |  2  |  1  |

y:   |  5  |  2  |  4  |  1  |  3  |
sa:  |  5  |  1  |  3  |  2  |  4  |

x:   |  2  |  3  |  2  |  3  |  1  |

k = 2
s:   |ab+ab|ba+ba|ab+a_|ba+__|a_+__|
oldx:|  2  |  3  |  2  |  3  |  1  |

y:   |  4  |  5  |  3  |  1  |  2  |
sa:  |  5  |  3  |  1  |  4  |  2  |

（\(oldx\) 是上一次的 \(x\)，那么也就是第一关键字的排名）。

由于只有两个关键字，所以可以用基数排序，比较难理解的是代码，可结合注释理解。

点击查看代码

void build() {
    for (int i = 1; i <= n; i++)
        c[x[i] = s[i]]++;
    // 初始只有一个字符时，每个子串的排名就是它的 ascii 码。
    for (int i = 2; i <= m; i++)
        c[i] += c[i - 1];
    // 根据计数排序，求前缀和后，值 x 的排名是 c[x-1]+1 ~ c[x]。
    for (int i = n; i; i--)
        sa[c[x[i]]--] = i;
    // 计数排序倒出来。
    for (int k = 1;; k <<= 1) {
        int num = 0;
        for (int i = n - k + 1; i <= n; i++)
            y[++num] = i;
        // 这些以 i 开头的子串没有第二关键字，排名最先。
        for (int i = 1; i <= n; i++)
            if (sa[i] > k)
                y[++num] = sa[i] - k;
        // 如果排名为 i 的长度为 k 的子串，前面还至少有 k 个字母，那么就可以成为第二关键字接上去。
        // 由于 sa 的定义，这样加入的排名是正确的。
        for (int i = 1; i <= m; i++)
            c[i] = 0;
        for (int i = 1; i <= n; i++)
            c[x[i]]++;
        for (int i = 2; i <= m; i++)
            c[i] += c[i - 1];
        // 将第一关键字丢进数组计数并做前缀和，和前面是同理的。
        for (int i = n; i; i--)
            sa[c[x[y[i]]]--] = y[i];
        // 同理
        swap(x, y);
        // 交换后，y[i] 的定义变为了第一关键字的起始点为 i 的排名。
        x[sa[1]] = num = 1;
        // 初始化，排名为 1 的子串的排名是 1。
        for (int i = 2; i <= n; i++)
            x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] and y[sa[i] + k] == y[sa[i - 1] + k] ? num : ++num);
        // 如果排名为 i 的子串的第一关键字和第二关键字（即排名为 i 的子串后面 k 个字母的子串）的排名都
        // 和前一个子串一样，那么就说明这两个子串相同，无需增加排名。
        m = num;
        // 还有多少个不同的子串。
        if (n == m)
            break;
        // 没有相同的，结束。
    }
}

二、求 height 数组

\(h_i=\operatorname{lcp}(s[sa_i\dots n],s[sa_{i-1}\dots n])\)，就是排名相邻的两个后缀，的最长公共前缀（LCP，Longest Common Prefix）。

定理

\[h_{x_i}\ge h_{x_{i-1}}-1 \]

证明：当 \(h_{x_{i-1}}\le 1\) 时，右边 \(\le 0\)，成立。

否则，由于 \(sa_{x_i}=i\)，那么可以得到后缀 \(i-1\) 和后缀 \(sa_{x_{i-1}-1}\) 有长度大于 \(1\) 的 LCP，假设这个 LCP 表示为 \(aA\)（\(a\) 是 \(s[i-1]\)，\(A\) 是一个 \(s[i\dots ?]\) 的串）。

那么后缀 \(i-1\) 就是 \(aAB\)，\(sa_{x_{i-1}-1}\) 就是 \(aAC\)，后缀 \(i\) 就是 \(AB\)，根据 \(sa\) 定义，有 \(B>C\)。

由于 \(sa_{x_i-1}\) 仅比后缀 \(i\) 排名小一位，而已经存在 \(AC<AB\)，所以 \(s[sa_{x_i-1}\dots n]\) 的开头也一定会是 \(A\)。

所以 \(h_{x_i}\) 的大小至少是 \(A\)，也就是 \(h_{x_{i-1}}-1\)。

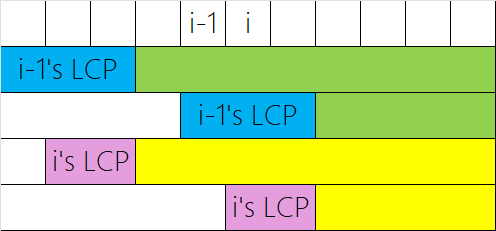
这里有一个感性理解图片。

所以至少是上一步减一。

然后对着定理暴力求即可。\(h_i\) 最多减小 \(n\) 次，最大为 \(n\)，故变化次数线性。

应用

求两个后缀的 LCP

\[\operatorname{lcp}(s[i\dots n],s[j\dots n])=\min_{k\in [i+1,j]}h_{x_k} \]

搞个 ST 表即可。