卡特兰数 & 题解：P3830 [SHOI2012] 随机树

第一问简单不说了，设 \(f_i\) 表示有 \(i\) 个叶子节点时的期望，直接转移即可。

有关第二问转移方程中 \(\frac{1}{i-1}\) 的证明，似乎没有看到卡特兰数方法的。

卡特兰数

\[C_n=\frac{1}{n+1}\binom{2n}{n} \]

公式一

通过拆式子，容易得到公式一：

\[C_n=\binom{2n}{n}-\binom{2n}{n-1}=\binom{2n}{n}-\binom{2n}{n+1} \]

穿越对角线问题

这个问题解释了卡特兰数的组合意义。

考虑这样一个问题：在平面直角坐标系中，从 \((0,0)\) 向上或向右走，走到 \((n,n)\)，不跨过直线 \(y=x\)，求方案数？

正难则反：用所有方案数减去跨过直线的方案数，可以得到从 \((0,0)\to (n,n)\) 要走 \(2n\) 步，其中选择 \(n\) 步向上走，故所有方案数是 \(\binom{2n}{n}\)。

接着考虑跨过直线的，把第一次跨过直线后的路径沿 \(y=x+1\) 对折，显然最后会到达 \((n+1,n-1)\)，对折前后的路径一一对应，方案数是 \(\binom{2n}{n-1}\)。

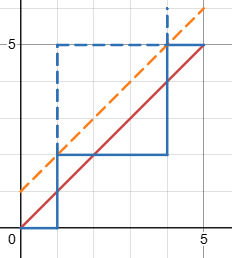
0/1 序列问题

组合意义一，可以把向右走看作 \(0\)，向上走看作 \(1\)，那么问题等价于求一个 \(01\) 序列，包含 \(n\) 个 \(0\) 和 \(n\) 个 \(1\)，且满足任意前缀 \(0\) 的数量不少于 \(1\) 的数量。那么这个问题的答案也是卡特兰数。

括号序列问题

求一个长度为 \(2n\) 的合法括号序列。一个右括号可以和前面出现过的一个左括号配对，因此这也是一个 \(0/1\) 序列问题，答案是卡特兰数。

公式二

\[C_n=\sum_{i=0}^{n-1}C_iC_{n-i-1},C_0=1 \]

这个公式可以由“二叉树问题”直观证明。

二叉树问题

求 \(n\) 个节点的二叉树有多少种方案数。

以下是 \(n=3\) 的情况，\(A\) 字头的是原树上的点，\(B\) 字头的是添加的点，令每个 \(A\) 字头的点都有两个儿子，除去根节点以外，新树共有 \(2n\) 个节点，并且一定有一半的节点是父亲的左子树，另一半是父亲的右子树，那么令位于左子树位置的是 \(\texttt{(}\)，右子树位置的是 \(\texttt{)}\)，先序遍历二叉树，显然有了左括号才能有右括号，转化为括号序列问题，这个问题的答案是 \(C_n\)。

设 \(F_x\) 表示新树有 \(x\) 个叶子节点时的方案数，其中 \(F_0=F_1=1\)，显然这棵树有 \((n+1)\) 个叶子节点，答案为 \(F_{n+1}\)。

可以枚举在根节点的左子树放 \(i\) 个叶子节点，右子树放 \((n-i)\) 个叶子节点，则有

\[F_n=\sum_{i=1}^{n-1}F_iF_{n-i} \]

故有 \(C_0=F_1,C_n=F_{n+1}\)，递推公式证明完成。

回到本题

本题证明 \(\frac{1}{i-1}\) 的难点，在于不知道每种二叉树生成的概率是否相同，而题目生成的二叉树就相当于上面的“新树”，由卡特兰数即可得知随机生成新树恰好只有 \(C_n\) 种情况，每种情况互不相同，故概率时相同的。