FHQ Treap 笔记

一、介绍

FHQ Treap 是一种 Treap，即对于一棵二叉树，每个节点存在

• 键值 \(key\)：点权大小，满足二叉搜索树性质；
• 随机值 \(rnd\)：满足小 / 大根堆性质。
• 此外还需维护字数大小 \(sz\)。

可以发现，对于任意的 \(key\) 和 \(rnd\) 值，总有一棵满足性质的 Treap。

FHQ Treap 的核心操作是分裂和合并。

1. 分裂

指的是给定一个 \(key\) 值 \(v\)，将 Treap 按 \(key\le v\) 还是 \(key>v\) 分成两棵 Treap，假设称作“小 Treap”和“大 Treap”。

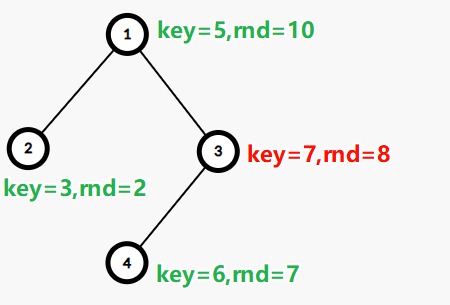
如对于这样一棵 Treap，按 \(v=6\) 分裂成两棵树，首先从根节点 \(1\) 开始递归，\(key_1=5\le 6\)，根据二叉搜索树性质，节点 \(1\) 及其左子树均应该属于“小 Treap”，因此让 \(1\) 成为“小 Treap”的根 \(L\)。

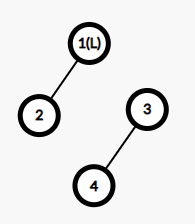
但是 \(1\) 的右子树内可能还存在满足 \(key\le 6\) 的（即上面的节点 \(4\)），这样的节点显然应该被挂在 \(1\) 的右子树，所以函数的写法就出来了。

void split(int rt, int v, int &l, int &r) { 
    // l 是如果当前节点属于小 Treap，应该位于哪里，r 同理。
    if (!rt) { // 分裂完了。
        l = r = 0;
        return;
    }
    if (t[rt].key <= v) { // rt 属于小 Treap。
        l = rt;
        split(t[rt].rs, v, t[rt].rs, r);
        // 如果 rt 在原 Treap 中的右子树内还有属于小 Treap 的 u，
        // u 在小 Treap 中应该被放在 rt 的右儿子。
    } else { // rt 属于大 Treap，同理。
        r = rt;
        split(t[rt].ls, v, l, t[rt].ls);
    }
    push_up(rt); // 下面会讲
}

2. 合并

有分裂才有合并，而分裂的定义使得两棵即将合并的 Treap 一定满足小 Treap 的 \(key\) 全部小于大 Treap 的，这使得合并时可以不考虑 \(key\)，只考虑 \(rnd\) 的大根堆性质。

具体地，对于一次合并，如果小 Treap 的优先级高，则小 Treap 的当前节点和左子树留下来，整个大 Treap 去和小 Treap 的右子树合并；如果大 Treap 的优先级高则相反。

int merge(int r1, int r2) {
    if (!r1 or !r2) // 其中一棵树合并完了。
        return r1 | r2; // 返回还剩下的那棵树。
    if (t[r1].rnd > t[r2].rnd) { // 小 Treap 优先级更高。
        t[r1].rs = merge(t[r1].rs, r2);
        push_up(r1);
        return r1;
    } else { // 大 Treap 优先级更高。
        t[r2].ls = merge(r1, t[r2].ls);
        push_up(r2);
        return r2;
    }
}

3. 维护 \(sz\)

这种近似线段树的对子树进行操作，维护 \(sz\) 只要写个 push_up 即可，split 和 merge 完都要 push_up。需注意根节点本身也有 \(1\) 大小。

void push_up(int rt) {
    t[rt].sz = t[t[rt].ls].sz + t[t[rt].rs].sz + 1;
}

4. 插入

假设插入一个节点满足 \(key=v\)，只需按 \(v\) 分裂，将小 Treap 和这个节点合并，再合并小 Treap 和大 Treap 即可。

void insert(int v) {
    split(root, v, x, y);
    root = merge(merge(x, newnode(v)), y);
}

5. 删除

假设删除一个节点满足 \(key=v\)，只需按 \(v\) 分裂得到小 Treap 和大 Treap，再按 \(v-1\) 分裂小 Treap 得到小小 Treap 和中 Treap。可以发现，中 Treap 的根就是要删除的节点，那么直接合并中 Treap 的根的左右子树，就可以得到删除节点后的中 Treap。接着再依次合并三个 Treap 即可。

void del(int v) {
    split(root, v, x, y);
    split(x, v - 1, x, z);
    root = merge(merge(x, merge(t[z].ls, t[z].rs)), y);
}

6. 求排名

假设求一个节点满足 \(key=v\) 的排名，只需按 \(v-1\) 分裂为小 Treap 和大 Treap，小 Treap 的 \(sz\) 加一就是排名。

int query_rk(int v) {
    split(root, v - 1, x, y);
    int ret = t[x].sz + 1;
    root = merge(x, y);
    return ret;
}

7. 给排名求值

类似值域线段树找第 \(k\) 小的操作。

int query_val(int rt, int rk) {
    if (t[t[rt].ls].sz + 1 == rk)
        return t[rt].key;
    if (t[t[rt].ls].sz >= rk)
        return query_val(t[rt].ls, rk);
    else
        return query_val(t[rt].rs, rk - t[t[rt].ls].sz - 1);
}

8. 求前驱

按 \(v-1\) 分裂，小 Treap 内排名最大的数就是前驱。

int query_pre(int v) {
    split(root, v - 1, x, y);
    int ret = query_val(x, t[x].sz);
    root = merge(x, y);
    return ret;
}

9. 求后继

按 \(v\) 分裂，大 Treap 内排名最小的数就是后继。

int query_nxt(int v) {
    split(root, v, x, y);
    int ret = query_val(y, 1);
    root = merge(x, y);
    return ret;
}

10. 完整代码

namespace FHQ {
    struct TREE {
        int ls, rs, sz, key, rnd;
    } t[N];
    int idx, root, x, y, z;
    void push_up(int rt) {
        t[rt].sz = t[t[rt].ls].sz + t[t[rt].rs].sz + 1;
    }
    void split(int rt, int v, int &l, int &r) {
        if (!rt) {
            l = r = 0;
            return;
        }
        if (t[rt].key <= v) {
            l = rt;
            split(t[rt].rs, v, t[rt].rs, r);
        } else {
            r = rt;
            split(t[rt].ls, v, l, t[rt].ls);
        }
        push_up(rt);
    }
    int merge(int r1, int r2) {
        if (!r1 or !r2)
            return r1 | r2;
        if (t[r1].rnd > t[r2].rnd) {
            t[r1].rs = merge(t[r1].rs, r2);
            push_up(r1);
            return r1;
        } else {
            t[r2].ls = merge(r1, t[r2].ls);
            push_up(r2);
            return r2;
        }
    }
    int newnode(int v) {
        t[++idx] = {0, 0, 1, v, rand()};
        return idx;
    }
    void insert(int v) {
        split(root, v, x, y);
        root = merge(merge(x, newnode(v)), y);
    }
    void del(int v) {
        split(root, v, x, y);
        split(x, v - 1, x, z);
        root = merge(merge(x, merge(t[z].ls, t[z].rs)), y);
    }
    int query_rk(int v) {
        split(root, v - 1, x, y);
        int ret = t[x].sz + 1;
        root = merge(x, y);
        return ret;
    }
    int query_val(int rt, int rk) {
        if (t[t[rt].ls].sz + 1 == rk)
            return t[rt].key;
        if (t[t[rt].ls].sz >= rk)
            return query_val(t[rt].ls, rk);
        else
            return query_val(t[rt].rs, rk - t[t[rt].ls].sz - 1);
    }
    int query_pre(int v) {
        split(root, v - 1, x, y);
        int ret = query_val(x, t[x].sz);
        root = merge(x, y);
        return ret;
    }
    int query_nxt(int v) {
        split(root, v, x, y);
        int ret = query_val(y, 1);
        root = merge(x, y);
        return ret;
    }
}
using namespace FHQ;

二、用 FHQ Treap 维护区间的情况

将区间的数按下标为 \(key\) 插进 Treap 里，因为下标单调递增所以事实上不用维护 \(key\)。分裂时，只要像主席树找第 \(k\) 小一样，按 \(sz\) 二分找即可。

细节是根节点也有 \(1\) 大小。

void split(int rt, int v, int &l, int &r) {
    if (!rt) {
        l = r = 0;
        return;
    }
    push_down(rt);
    if (t[t[rt].ls].sz + 1 <= v) {
        l = rt;
        split(t[rt].rs, v - t[t[rt].ls].sz - 1, t[rt].rs, r);
    } else {
        r = rt;
        split(t[rt].ls, v, l, t[rt].ls);
    }
    push_up(rt);
}

翻转某个区间的话，拆出这个区间的树，然后从根节点开始，每个节点都交换左右儿子，就能达到翻转区间的效果。

其它的区间操作就和线段树一样了。