状压 DP & 轮廓线 DP & 插头 DP 笔记

我本以为我很会这玩意的，不就是将集合取或不取设为状态，几个集合转移而已嘛！然后我就被一群题爆杀了。

一、普通状压

1. P2157 [SDOI2009] 学校食堂

首先有个结论：\(a\operatorname{or} b-a\operatorname{and} b=a\operatorname{xor} b\)。

虽然人数很多，但事实上关心第 \(i\) 个人打饭贡献的只有它前后八个人，可以设计一种 dp 状态，在处理第 \(i\) 个人时强制前 \(i\) 个人已经全部打好饭，这样子第 \(i\) 个人的打饭贡献虽然还是受前后八个人干预，但是打饭的顺序就只和他后面八个人有关了，所以就可以设计状态 \(f_{i,s,j}\) 表示前 \(i - 1\) 个人打完饭，最后一个打的是 \(i+j\) 号（\(-7\le j\le 8\)），而它后面的八个人是否已经打饭的状压是 \(s\)。

那么有三种选择：

• 让 \(i\) 打饭，

f[i + 1][s >> 1][j - 1 + 8] = min(f[i + 1][s >> 1][j - 1 + 8], f[i][s][j + 8]);

• 让 \(i\) 后面的人打饭，注意需要需要满足 \(i+1\sim i+j-1\) 都能容忍 \(i+j\) 先打饭。

f[i][s | 1 << k][k + 8] = min(f[i][s | 1 << k][k + 8], f[i][s][j + 8] + (t[i + j] ^ t[i + k]));

• 特殊情况，\(i\) 前面没有任何人打过饭。

f[i][s | 1 << k][k + 8] = min(f[i][s | 1 << k][k + 8], f[i][s][j + 8]);

时间复杂度 \(O(2^8\times 16\times n)\)。

2. P3092 [USACO13NOV] No Change G

首先看数据范围，肯定是对硬币状压，那么只需要知道每种硬币组合能不能买完所有物品，再在每组合法的硬币组合中取一个剩的钱最多的就好了。

设 \(f_s\) 表示硬币组合 \(s\) 最多能买到哪个物品，对于状态 \(s\) 推往下一个状态，在价格前缀和上二分，看一下多了一个硬币之后能买到哪个数就行了。

时间复杂度 \(O(2^k\log n)\)。

二、轮廓线 dp

有时候会发现，在二维表格上，\((i,j)\) 的状态不一定和每一个 \((i-1,k)\) 无关，但他和 \((i-1,p)\)（\(p\ge j\)）和 \((i-1,q)\)（\(q<j\)）有关，而这个轮廓线事实上也可以用一个二进制状态表现并容易维护（如把轮廓线最高位设为最新加入的格子，轮廓线在二维表格上向右走一步，就相当于最高位加数，最低位被顶掉）这个时候就称作轮廓线 dp。

1. P7171 [COCI 2020/2021 #3] Selotejp

理解上面的“轮廓线”后，设 \(f_{i,j,s}\) 表示处理到 \((i,j)\)，轮廓线状态为 \(s\)，其中 \(0\) 是横着贴或不能贴，\(1\) 是竖着贴，的方案数。

• 不能贴，直接更新。

f[x][y][s >> 1] = min(f[x][y][s >> 1], f[i][j][s]);

• 如果左边一格存在，是能贴的，是横着走的，那就可以接着横着贴；否则也可以自己从头开始横着贴。

if (y and ch[i][j] == '#' and !((s >> m - 1) & 1))
    f[x][y][s >> 1] = min(f[x][y][s >> 1], f[i][j][s]);
else
    f[x][y][s >> 1] = min(f[x][y][s >> 1], f[i][j][s] + 1);

• 竖着贴也是差不多的。

if (x and (s & 1))
    f[x][y][s >> 1 | (1 << m - 1)] = min(f[x][y][s >> 1 | (1 << m - 1)], f[i][j][s]);
else
    f[x][y][s >> 1 | (1 << m - 1)] = min(f[x][y][s >> 1 | (1 << m - 1)], f[i][j][s] + 1);

时间复杂度 \(O(2^mnm)\)。

2. P4363 [九省联考 2018] 一双木棋 chess

首先，棋盘的形状肯定是靠在左上角的一个锯齿状的东西，考虑从最左下角的点的左边开始，\(1\) 表示向右走，\(0\) 表示到达行末并向上走，一直到达右上角的点的上边，初始的状态显然是 \(000\dots 111\dots\)。

然后博弈论得是倒着取最优，所以要把棋盘中心对称旋转。

至于转移顺序，可以发现放一个棋子，就相当于交换了状态中的一组相邻的 \(01\)，提前处理好转移顺序并拓扑排序即可。

时间复杂度 \(O(2^{n+m}(n+m))\)。

三、插头 DP

1. 多条回路

P5074 Eat the Trees。

对于一条回路，回路上的每个格子的四条边，必然只有两条边和回路接触（一进一出）。那么借用轮廓线 DP 的思路，设 \(f_{i,j,s}\) 表示处理完 \((i,j)\)，轮廓线状态为 \(s\)。假如已经知道了左边和上边的画法，那么这一格的画法就会有六种情况。

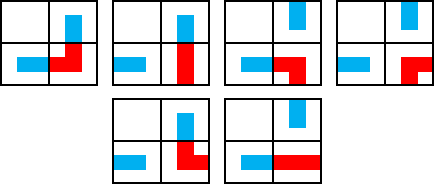
那么，状态数为 \(O(6^m)\)，显然无法接受，观察轮廓线，真的需要存四个方向六种状态吗？

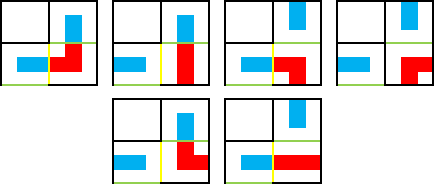
观察轮廓线，只有绿色的需要存是否存在向下方向，黄色的需要存是否存在向右方向。

假设都只用一位二进制表示，向左表示 \(0\)，向右表示 \(1\)；向上表示 \(0\)，向下表示 \(1\)。观察这些轮廓线转移前后的变化。

注意：一般的状压，二进制最低位（最右边）对应从左往右第一列，本图为了便于观察，二进制最左边对应从左往右第一列。

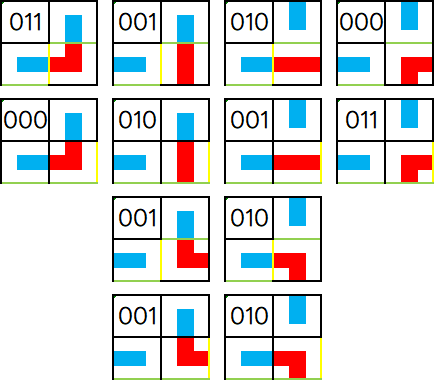
可以发现：原本取本列（从 \(1\) 开始编号）和本列的前一位（二进制从第 \(0\) 位开始），如果两个数不同，那么就可以额外向相同的状态转移，否则都可以向这两位异或的状态转移。

四、最小斯坦纳树

1. AT_abc395_g [ABC395G] Minimum Steiner Tree 2

我觉得先理解这个题还更容易理解模板啊！

有两个非固定点，考虑枚举每个第一个非固定点，把他当作固定点，预处理其对应所有第二个非固定点的答案，\(O(1)\) 回答。

设 \(f_{s,i}\) 表示经过固定点集合为 \(s\)，此外到达节点 \(i\) 的最小花费。

对于固定 \(i\)，枚举子集；对于固定 \(s\)，Floyd。

for (int s = 1; s < 1 << k + 1; s++) {
    for (int i = 1; i <= n; i++)
        for (int t = s; t; t = s & (t - 1))
            f[s][i] = min(f[s][i], f[t][i] + f[s ^ t][i]);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            f[s][i] = min(f[s][i], f[s][j] + dis[j][i]);
}

对于第二个非固定点是 \(i\)，答案显然是 f[(1 << k + 1) - 1][i]，离线存储下来。

时间复杂度 \(O(2^k\times n^3)\)，如果用 Dijkstra，可以少一个 \(n\) 多一个 \(\log\)，但是意义不大。

2. P6192 【模板】最小斯坦纳树

这时，把非固定点理解成“跳板”即可。

五、根号分治 + 状压

1. P2150 [NOI2015] 寿司晚宴

发现 \(23\times 29>500\)，所以每一个数最多只有可能有一个大于等于 \(23\) 的质数，比 \(23\) 小的质数只有 \(8\) 个，对于大质数相同的，一起处理，设 \(f1_{s,t}\) 表示第一个人取 \(s\) 质数集合，第二个人取 \(t\) 质数集合，并且大质数给 \(1\) 的方案数，\(f2_{s,t}\) 则是大质数给第二个人，转移即可。

当处理完大质数相同的时候，合并进总答案。

总复杂度 \(O(2^8\times n)\)

2. P8292 [省选联考 2022] 卡牌

如果质数个数较小，只需大力容斥即可，用总方案减去所有不合法的方案：钦定覆盖 \(0\) 个质数 \(-\) 钦定覆盖 \(1\) 个质数 \(+\) 钦定覆盖 \(2\) 个质数……

但是质数个数很多，但又不算多，根据 NOI2015 寿司题经验，可以发现 \(43\times 47>2000\)，也就是说每一个数最多只有一个大于 \(43\) 的质数，所以考虑根号分治。

考虑只有大质数怎么做，那么直接枚举给出的卡牌序列里整除大质数 \(p\) 的个数 \(f_p\)，然后如果要求被大质数 \(p\) 整除，那么这 \(f_p\) 个卡牌不能全不选，\(2^{f_p}-1\)，否则就放养，\(2^{f_p}\)。

接下来只需要把第一段和第三段结合起来，即对每种不同的小质数集合都算一次大质数的答案，容斥即可。