莫队 笔记
本文原在 2024-04-03 17:04 发布于本人洛谷博客。
一、普通莫队
1. 介绍
莫队是一种用来解决如下问题的算法:
-
只有查询,没有修改。
-
可以离线。
-
已知区间 \([l,r]\) 的答案,可以 \(O(1)\) 转移到 \([l\pm 1,r]\) 或 \([l,r\pm 1]\)。
2. 实现
用两个指针 \(l\),\(r\) 暴力从上一个查询区间一步一步转移到下一个区间。
但是,如果所有的查询区间都在极限拉扯(如第一个查询 \([1,n]\),第二个查询 \([n-1,n]\),第三个又查询 \([1,n]\)……),时间复杂度就会退化到和暴力一样的 \(O(nm)\)。
所以我们考虑优化:把数列分块,分成 \(\sqrt n\) 个块,然后先把左端点在一个块内的查询完再查询下一个块。左端点在同一个块的就让右端点从小到大排序。
3. 块长
当 \(n,m\) 同阶时,块长 \(block=\sqrt n\) 时时间复杂度最优。
当 \(n,m\) 不同阶时,块长 \(block=\left\lfloor \frac{n^2}{m}\right\rfloor\) 时时间复杂度最优。
4. 例题
P2709 小 B 的询问
有一个长为 \(n\) 的整数序列 \(a\),值域为 \([1,k]\)。 一共有 \(m\) 个询问,每个询问给定一个区间 \([l,r]\),求:
其中 \(c_i\) 表示数字 \(i\) 在 \([l,r]\) 中的出现次数。
当即将增加一个数时(此时还没更改 \(c\) 的值),\(ans=ans-c_i^2+(c_i+1)^2\)。
删去时同理,\(ans=ans-c_i^2+(c_i-1)^2\)。
核心代码(\(a\) 为原数组,\(belong,block\) 为分块,\(cnt\) 为统计出现个数的数组,\(tmp\) 统计当前区间的答案):
namespace MoDui {
bool cmp(QUESTION x, QUESTION y) {
return belong[x.l] != belong[y.l] ? belong[x.l] < belong[y.l] : x.r < y.r;
}
void init_block() {
block = sqrt(n);
for (int i = 1; i <= n; i++) belong[i] = (i - 1) / block + 1;
}
void add(int x) {
tmp -= cnt[a[x]] * cnt[a[x]];
cnt[a[x]]++;
tmp += cnt[a[x]] * cnt[a[x]];
}
void del(int x) {
tmp -= cnt[a[x]] * cnt[a[x]];
cnt[a[x]]--;
tmp += cnt[a[x]] * cnt[a[x]];
}
void solve() {
sort(q + 1, q + m + 1, cmp);
int l = 1, r = 0;
for (int i = 1; i <= m; i++) {
while (l > q[i].l) add(--l);
while (l < q[i].l) del(l++);
while (r < q[i].r) add(++r);
while (r > q[i].r) del(r--);
ans[q[i].id] = tmp;
}
}
}
using namespace MoDui;
二、回滚莫队
1. 介绍
回滚莫队用于解决增加 \(O(1)\) 而删除不是 \(O(1)\) 的莫队问题。
2. 实现
-
以与普通莫队同样的方法排序。
-
当询问左右端点 \(q_l,q_r\),在同一个块时,暴力求解。
-
这里的 \(l\) 不再移动到 \(q_l\),而是 \(q_l\) 所在的块的下一个块的左端点。
-
当两次询问的 \(q_l\) 在同一个块内时,由于 \(q_r\) 升序,可以直接移动 \(r\),往后加,在暴力计算区间 \([q_l,l-1]\) 的答案。
-
当 \(q_l\) 到下一个块时,直接暴力将 \([l,r]\) 的结果全部删除,答案清零。
-
由于只增不删(或只删不增)并且不能在 \(O(1)\) 内处理删(或增),因此 del(或 add)函数不再处理统计答案。
3. 例题
AT_joisc2014_c 歴史の研究
给定一个长度为 \(n\),值域为 \([1,10^9]\) 的数列 \(a\)。\(m\) 次询问求区间 \([l,r]\) 中的:
其中 \(c\) 表示该数在这个区间内出现的次数。
求最大操作增加容易,删除却很难,所以考虑回滚莫队。
由于值域较大,还需离散化。
核心代码:
namespace MoDui {
void add(int x) {
cnt[a[x]]++;
tmp = max(tmp, val[a[x]] * cnt[a[x]]);
}
void del(int x) { cnt[a[x]]--; }
void solve() {
sort(q + 1, q + m + 1, cmp);
int l = 1, r = 0;
for (int i = 1; i <= m; i++) {
if (q[i].l >= l) {
tmp = 0;
for (int j = l; j <= r; j++) del(j);
r = belong[q[i].l] * block;
l = r + 1;
}
if (belong[q[i].l] == belong[q[i].r]) {
for (int j = q[i].l; j <= q[i].r; j++) add(j);
ans[q[i].id] = tmp;
for (int j = q[i].l; j <= q[i].r; j++) del(j);
tmp = 0;
continue;
}
while (r < q[i].r) add(++r);
int last = tmp;
for (int j = q[i].l; j < l; j++) add(j);
ans[q[i].id] = tmp;
for (int j = q[i].l; j < l; j++) del(j);
tmp = last;
}
}
}
using namespace MoDui;
三、树上莫队
0. 前置知识:欧拉序
如用先序遍历遍历这一棵树:
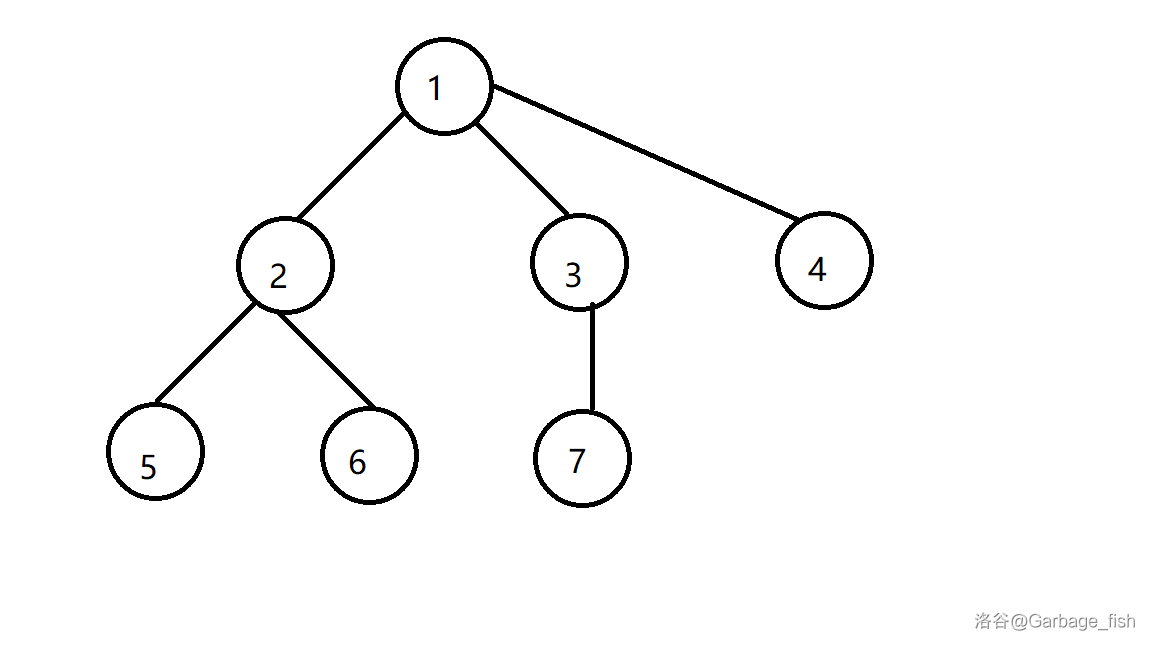
序列为:1 2 5 6 3 7 4
欧拉序与先序遍历的不同点在于:当一个节点的所有子树已经遍历完时,再次将这个节点加入序列中。
则上图的欧拉序为:1 2 5 5 6 6 2 3 7 7 3 4 4 1
粗体字组成的序列与先序遍历序列一致。
1. 介绍
树上莫队常用于解决树上路径或子树区间相关的问题。
2. 实现
对上上面的这个序列进行分析,假设 \(u\) 和 \(v\) 的 LCA 为 \(l\)。
当 \(u\ne l,v\ne l\) 时:
假设 \(u=5,v=4\),则 \(l=1\),他们之间的最短路径为 5 2 1 4,而选取欧拉序中出现较早的点第二次出现的,到另一个点第一次出现的部分:
5 6 6 2 3 7 7 3 4
容易发现序列中没有 \(l\),而出现了 \(1\) 次的点都位于最短路径中,出现了 \(2\) 次的点都不属于最短路径中,因此只需要统计出现了一次的点的答案,再额外计算 \(l\)。
当 \(u\) 或 \(v\) 等于 \(l\) 时:
假设 \(u=6,v=1\),则 \(l=1\),他们之间的最短路径为 5 2 1,而选取欧拉序中等于 \(l\) 的点的第一次出现的,到另一个点第一次出现的部分:
1 2 5 5 6
发现序列中出现了一次的点全部属于答案,直接统计即可。
3. 例题
SP10107 COT2 - Count on a tree II
有 \(n\) 个节点的树,有 \(2\times 10^9\) 种颜色,每个节点有一种颜色。\(m\) 次询问,求 \(u\to v\) 路径上有多少个不同颜色的点。
离散化+树上莫队。
核心代码:
namespace MoDui {
bool cmp(QUESTION x, QUESTION y) {
if (belong[x.l] != belong[y.l]) return belong[x.l] < belong[y.l];
if (belong[x.l] % 2) return x.r < y.r;
return x.r > y.r;
}
void dfs(int u, int fa) {
dfn[++timestamp] = u;
st[u] = timestamp;
f[u][0] = fa;
for (int i = 1; i <= 20; i++) f[u][i] = f[f[u][i - 1]][i - 1];
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].v;
if (v == fa) continue;
dfs(v, u);
}
dfn[++timestamp] = u;
en[u] = timestamp;
}
int lca(int x, int y) {
if (x == y) return x;
if (st[x] < st[y]) swap(x, y);
for (int i = 20; i >= 0; i--)
if (st[f[x][i]] > st[y]) x = f[x][i];
return f[x][0];
}
void add(int x) {
vis[x]++;
if (vis[x] == 1) {
cnt[a[x]]++;
if (cnt[a[x]] == 1) tmp++;
}
if (vis[x] == 2) {
cnt[a[x]]--;
if (!cnt[a[x]]) tmp--;
}
}
void del(int x) {
if (vis[x] == 1) {
if (cnt[a[x]] == 1) tmp--;
cnt[a[x]]--;
}
if (vis[x] == 2) {
if (!cnt[a[x]]) tmp++;
cnt[a[x]]++;
}
vis[x]--;
}
void get_question() {
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
if (st[u] > st[v]) swap(u, v);
int tmp = lca(u, v);
if (tmp == u) q[i] = {st[u], st[v], i, 0};
else q[i] = {en[u], st[v], i, tmp};
}
}
void solve() {
sort(q + 1, q + m + 1, cmp);
int r = 0, l = 1;
for (int i = 1; i <= m; i++) {
while (l > q[i].l) add(dfn[--l]);
while (l < q[i].l) del(dfn[l++]);
while (r < q[i].r) add(dfn[++r]);
while (r > q[i].r) del(dfn[r--]);
if (q[i].lca) add(q[i].lca);
ans[q[i].id] = tmp;
if (q[i].lca) del(q[i].lca);
}
}
}
using namespace MoDui;
四、带修莫队
1. 介绍
用于解决带有单点修改的莫队问题。
2. 实现
将询问 \([l,r]\) 加上一维 \(t\) 表示时间,变为 \([l,r,t]\)。
则可以 \(O(1)\) 转移 \([l\pm 1,r,t],[l,r\pm 1,t],[l,r,t\pm 1]\)。
只需要在写一个函数处理 \(t\) 的修改即可。
需要注意的是,最优块长为 \(n^{\frac{2}{3}}\),排序函数也有所更改。
3. 例题
P1903 [国家集训队] 数颜色 / 维护队列
给定一个长度为 \(n\),值域为 \([1,10^6]\) 的数列 \(a\)。进行 \(m\) 次操作:
-
\(Q\) \(L\) \(R\),表示求第 \(L\) 到第 \(R\) 个数有多少个互不相同的数。
-
\(R\) \(P\) \(C\),表示将第 \(p\) 个数改为 \(C\)。
核心代码:
namespace MoDui {
bool cmp(QUESTION x, QUESTION y) {
if (belong[x.l] != belong[y.l]) return x.l < y.l;
if (belong[x.r] != belong[y.r]) return x.r < y.r;
return x.t < y.t;
}
void add(int x) {
if (!cnt[x]) tmp++;
cnt[x]++;
}
void del(int x) {
cnt[x]--;
if (!cnt[x]) tmp--;
}
void update(int t, int x) {
if (q[x].l <= upd[t].p and upd[t].p <= q[x].r) {
add(upd[t].x);
del(a[upd[t].p]);
}
swap(upd[t].x, a[upd[t].p]);
}
void solve() {
sort(q + 1, q + qcnt + 1, cmp);
int l = 1, r = 0, t = 0;
for (int i = 1; i <= qcnt; i++) {
while (l > q[i].l) add(a[--l]);
while (l < q[i].l) del(a[l++]);
while (r < q[i].r) add(a[++r]);
while (r > q[i].r) del(a[r--]);
while (t < q[i].t) update(++t, i);
while (t > q[i].t) update(t--, i);
ans[q[i].id] = tmp;
}
}
}
using namespace MoDui;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号