FFT 笔记
本文原在 2025-01-30 00:34 发布于本人洛谷博客。
参考:yyc dalao 的讲课 ppt,wzr dalao 的博客。
一、前置知识
1. 多项式
就是初中课本上说的多项式,但是只有“一元”,如 \(x^2+2x+3\) 是一个二次多项式。
那么对于一个 \(n\) 次多项式 \(A(x)\),可表示为:
下文无特殊说明,均用小写字母表示一个对应大写字母多项式的系数
2. 卷积
设 \(\oplus\) 是任意运算符,若已知多项式 \(A(x),B(x)\),求多项式 \(C(x)\) 有如下运算:
则称为“\(\oplus\) 卷积”。
如我们熟知的两个多项式相乘,就是一种“加卷积”。
如 \((x^2+2x+3)(x-1)\),设前面是 \(A(x)\),后面是 \(B(x)\),则 \(a=\{3,2,1\},b=\{-1,1\}\)。
求得 \(c=\{a_0b_0,a_0b_1+a_1b_0,a_1b_1+a_2b_0,a_2b_1\}\),即 \(\{-3,1,1,1\}\),上述式子也恰好是 \(x^3+x^2+x-3\)。
3. 点值 / 插值
点值就是多项式取特值时的值。
由初中函数知识,可以知道 \(n\) 次多项式只需 \((n+1)\) 个不同的点和点值就能确定全部系数,这个过程叫插值。
4. 复数
(1). 定义
定义 \(i^2=-1\),即 \(\sqrt{-1}=i\)。
称 \(i\) 为虚数,实数和虚数统称复数。
虚数的一般式:\(z=a+bi(a\in \R,b\in\R,b\ne 0)\)。(\(\R\) 是实数集合)
(2). 复平面
将 \(z\) 的 \((a,b)\) 拍到平面直角坐标系上,即复平面。
复平面上一个点对应一个虚数。
连接原点 \((0,0)\),线段长 \(r\) 称作模长,即 \(\sqrt{a^2+b^2}\)。
线段与 \(x\) 轴正半轴夹角 \(\theta\) 称作幅角。
有欧拉公式 \(z=r(\cos\theta+i\sin\theta)\)。
证明:\(z=a+bi=r(\frac{a}{r}+i\frac{b}{r})=r(\cos\theta+i\sin\theta)\)
(3). 四则运算
和实数四则运算一致,将 \(i\) 视作未知数即可,但是 \(i^2\) 需变成 \(-1\)。
若有 \(z_1=a+bi,z_2=c+di\)。
对于乘法,有棣莫弗定理
- 两复数相乘,模长相乘,幅角相加。
证明不高深,就是暴力拆式子再合回去,不写了。
5. 弧度制
圆心角(可以大于 \(180\degree\))所对的弧,与半径的比值。
易得 \(180\degree\) 对应的是 \(\pi\)。
弧度制可以直接上 \(\sin\) 等三角函数。
6. 单位根
(1). 定义
若 \(\omega_n^0\ne\omega_n^1\ne\dots\ne\omega_n^{n-1}\) 成立,且 \(\omega_n^n=1\),则称 \(\omega_n\) 称作 \(n\) 次本原单位根。
不要看串了,这里都是指的 \(\omega_n\) 这一个数。
(2). 构造
由于虚数相乘幅角相加,所以一个简单的想法是在复平面上以原点为圆心画个半径为 \(1\) 的圆,让 \(\omega_n\) 在上面一直乘,转个圈就好了。(因为 \(\omega_n^0=\omega_n^n=1\),所以最后一定会转回 \(x\) 轴正半轴才能是实数)
这个圆的周长是 \(2\pi\),平分给 \(n\) 段弧就是每段弧长为 \(\frac{2\pi}{n}\)。由上文提到的欧拉公式,有一种简单的构造:
我也不知道哪里画复平面啊,直接偷 yyc 的图了:
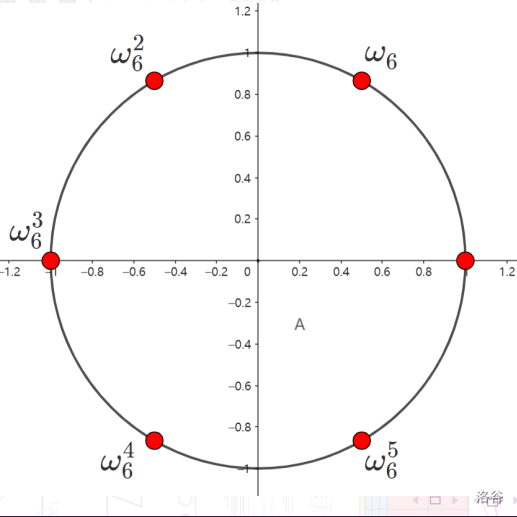
(3). 性质
结合上图可知:
-
\(\omega_n^k=\omega_n^{n+k}\)。
-
\(\omega_n^{n\div 2}=-1\)。
这样的特殊性将有利于我们做 FFT。
二、FFT
1. 简述
就是求 \(C(x)=A(x)B(x)\)(加卷积)。假设 \(A(x)\) 是 \(n\) 次多项式,\(B(x)\) 是 \(m\) 次多项式。易得 \(C(x)\) 是 \((n+m)\) 次多项式,令 \(p=n+m\)。
由点值和插值的知识,可以从 \(A(x),B(x)\) 中选出 \((p+1)\) 个点求点值,并对应位置点值相乘得到这么多个点积,这些点积一定在 \(C(x)\) 上,插值就可以求到 \(C(x)\)。
所以现在问题变成了:快速的求点值(DFT),快速的插值(IDFT)。
2. DFT
对于 \(A(x)=\sum_{i=1}^na_ix^i\),将其按次数奇偶拆成两份,并“降次”:
你可以发现
接着考虑把我们的单位根知识喂进去,根据学长的笔记,如果将 \(\omega_p\) 的每个次幂带进去,或许能带来一些方便。
代入 \(\omega_n^k\):
有个小 bug,\(2k>n\) 怎么办?\(\omega_n^{2k}=\omega_n^{2k-n}\)。
对于填进 \(A_0(x),A_1(x)\) 里的,就相当于 \((\omega_n^{k})^2\div(\omega_n^{n\div 2})^2\),后面的除数就是 \((-1)^2\)(前面讲过),故不影响。
而对于 \(A_1(x)\) 的系数,此时就不能是 \(\omega_n^k\) 了,而应该是 \(\omega_n^{(2k-n)\div 2}\),即 \(\omega_n^{k-n\div 2}\),那显然就是符号从 \(+\to -\)。
注意到 \(\omega_n^{2k}=\omega_{n\div 2}^k\),因为把圆分成 \(n\) 份拿 \(2k\) 份等价于分成 \(\frac{n}{2}\) 份拿 \(k\) 份。
所以就可以愉快的分治了!!!
但是这不是线段树,不能瞎分,所以得把 \(p\) 补成 \(2\) 的若干次幂再分治。直接把高位系数填 \(0\) 就好了。
3. IDFT
我这个水平推 ** 呢,感兴趣的移步 P3803 题解区,出结论:
对点积做一次 DFT,然后把 \([1,n]\) 翻转,再除以长度 \(n\),即可完成 IDFT。
4. 优化
首先经典优化:用 STL 小心被卡常,手写复数类。
递归的时候定义太多数组,时空肯定不优。
直接拿出观察力:
要求 \([0,1,2,3,4,5,6,7]\)。
-
求 \([0,2,4,6]\)。
- 求 \([0,4]\):求 \([0]\),再求 \([4]\)。
- 求 \([2,6]\):求 \([2]\),再求 \([6]\)。
-
求 \([1,3,5,7]\)。
- 求 \([1,5]\),求 \([1]\),再求 \([5]\)。
- 求 \([3,7]\),求 \([3]\),再求 \([7]\)。
顺序为:\([0,4,2,6,1,3,5,7]\)。
对应二进制:\([000,100,010,110,001,101,011,111]\)。
而原序列的:\([000,001,010,011,100,101,110,111]\)。
所以就是二进制颠倒一下就能递推了!
二进制颠倒的式子递推求:假设我们知道当前二进制数,去掉最后一位的颠倒数,我们将这个颠倒数右移一位,把开头设成当前二进制数的最后一位就行了。说的有点抽象,上代码!
#include <bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
const int N = 4e6 + 10;
const double pi = acos(-1);
int n, m, r[N];
struct Complex {
double x, y;
const Complex operator+(const Complex &tmp) const {
return {x + tmp.x, y + tmp.y};
}
const Complex operator-(const Complex &tmp) const {
return {x - tmp.x, y - tmp.y};
}
const Complex operator*(const Complex &tmp) const {
return {x * tmp.x - y * tmp.y, x * tmp.y + tmp.x * y};
}
} a[N], b[N], c[N], p[N];
void fft(int mx, Complex *a) {
for (int i = 0; i < 1 << mx; i++)
if (i < r[i])
swap(a[i], a[r[i]]);
for (int i = 0; i < mx; i++) {
Complex w = {cos(pi / (1 << i)), sin(pi / (1 << i))};
p[0] = {1, 0};
for (int j = 1; j < 1 << i; j++)
p[j] = p[j - 1] * w;
for (int j = 0; j < 1 << mx; j++) {
if (!(j & (1 << i))) {
Complex a1 = a[j], a2 = a[j + (1 << i)], tmp = a2 * p[j & ((1 << i) - 1)];
a[j] = a1 + tmp;
a[j + (1 << i)] = a1 - tmp;
}
}
}
}
signed main() {
IOS;
cin >> n >> m;
for (int i = 0; i <= n; i++)
cin >> a[i].x;
for (int i = 0; i <= m; i++)
cin >> b[i].x;
int mx = 1;
while ((1 << mx) <= n + m)
mx++;
for (int i = 1; i < 1 << mx; i++)
r[i] = (r[i >> 1] >> 1) | ((i & 1) << (mx - 1)); // 颠倒
fft(mx, a);
fft(mx, b);
for (int i = 0; i < 1 << mx; i++)
c[i] = a[i] * b[i];
fft(mx, c);
reverse(c + 1, c + (1 << mx));
for (int i = 0; i <= n + m; i++)
cout << (int)(c[i].x / (1 << mx) + 0.5) << " "; // 向上取整防止精度问题
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号