点分治 & 点分树 笔记

本文原在 2024-07-26 09:12 发布于本人洛谷博客，于 2025-3 重构。

点分治

1. 介绍

点分治常用于解决树上路径数目，符合条件的点对数目的问题。

2. 实现

先看例题：

P4178 Tree

给定一棵 \(n\) 个节点的树，每条边有边权，求出树上两点距离小于等于 \(k\) 的点对数量。

(0). 大体思路

找到一棵树的重心，然后统计经过重心的路径数目，然后再分治所有的子树。

由于找的都是重心，所以时间复杂度 \(O(n\log n)\)。

(1). 找根

由于处理重心，所以要先写一个函数找重心。

我们知道，以重心为根，重心最大的子树的大小，是绝对小于以非重心为根，那个点的最大子树大小的，所以我们只需要处理每个点的子树大小 \(sz\)，和该点最大的子树的大小 \(mx\) 即可。

需要注意的是，节点 \(u\) 的上方也是一棵子树，而该子树的大小为 \(nodeCnt-sz_u\)，其中 \(nodeCnt\) 表示整棵树的大小。

Code：

void getrt(int u, int fa, int nodecnt) {
    sz[u] = 1;
    mx[u] = 0;
    for (int i = head[u]; i; i = edge[i].next) {
        int v = edge[i].v;
        if (v == fa or vis[v]) continue;
        getrt(v, u, nodecnt);
        sz[u] += sz[v];
        mx[u] = max(mx[u], sz[v]);
    }
    mx[u] = max(mx[u], nodecnt - sz[u]);
    if (mx[u] < mx[rt]) rt = u;
}

(2). 处理每个点到重心的距离

既然要处理经过重心，且距离小于等于 \(k\) 的路径，则必须要先求出每个点到根节点的路径，深搜遍历一次即可。

Code：

void getdis(int u, int fa, int dis) {
    q[++p] = dis;
    for (int i = head[u]; i; i = edge[i].next) {
        int v = edge[i].v;
        if (v == fa or vis[v]) continue;
        getdis(v, u, dis + edge[i].w);
    }
}

(3). 计算+递归

在上一步中，我们把每个点到重心的距离存入了一个 \(q\) 数组，如果某个点到重心的距离为 \(q_i\)，则答案明显为 \(q\) 数组中，小于等于 \(k-q_i\) 的数的数量。

但是，我们发现这样会算重：

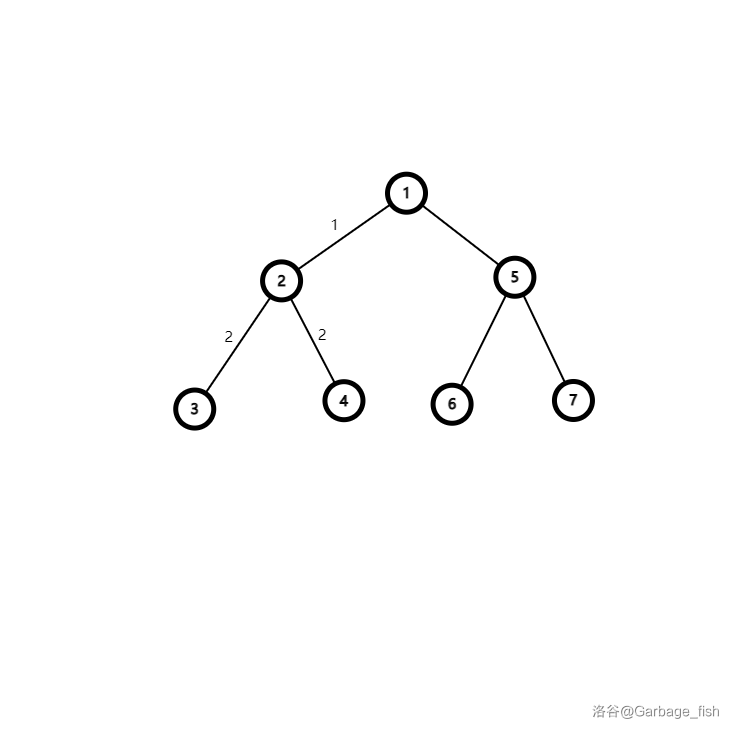
如上图所示，如果 \(k=6\)，则 \(3-2-1-2-4\) 会被计算一次，而 \(3-2-4\) 时又会计算一次。

我们发现，这些重复的路径都满足经过他的子节点 \(2\)，所以减去经过他的子节点的即可。

Code：

int calc() {
    int ret = 0;
    sort(q + 1, q + p + 1);
    for (int i = 1; i < p; i++)
        ret += upper_bound(q + i + 1, q + p + 1, k - q[i]) - (q + i + 1);
    return ret;
}
void solve(int u, int nodecnt) {
    mx[rt = 0] = oo;
    getrt(u, 0, nodecnt);
    getrt(rt, 0, nodecnt);
    p = 0;
    getdis(rt, 0, 0);
    ans += calc();
    vis[rt] = 1;
    for (int i = head[rt]; i; i = edge[i].next) {
        int v = edge[i].v;
        if (vis[v]) continue;
        p = 0;
        getdis(v, rt, edge[i].w);
        ans -= calc();
        solve(v, sz[v]);
    }
}

3. 刷题总结

(1). P4183 [USACO18JAN] Cow at Large P

对于一个点 \(u\)，农民能够守住的点 \(v\) 应该满足以下条件：

\[\operatorname{dis}(u,v)\le\operatorname{dis}(\operatorname{le}_v,v) \]

其中 \(\operatorname{le}\) 表示一个节点最近的叶子，这个只需要两次 dfs 用近似换根 dp 的思路就可以容易的求出来 \(\operatorname{le_u}\) 和对应的 \(\operatorname{dis}(\operatorname{le}_u,u)\)。

这样子就转换成了就满足关系的点对数，和上面的例题一样，每次分治只统计满足下面条件的 \((u,v)\)，就是 \(u\to v\) 的路径穿过了当前的重心。

假设从重心到 \(u\) 的距离为 \(d_u\)，上面的条件转化成了：

\[d_u+d_v\le \operatorname{dis}(\operatorname{le}_v,v) \]

即

\[d_u\le \operatorname{dis}(\operatorname{le}_v,v)-d_v \]

开两个桶，分别统计，再容斥掉来自同一子树的答案即可。

但是这样会有个问题，对于一个满足条件的点 \(v\)，它的子树内的所有点都不需要被值守。

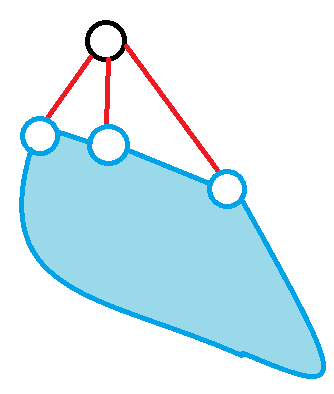
如图，蓝色填充区域都被重复计算了。

也就是说，我们希望得到一种差分，给每个节点安上一个点权，使得对于每个子树，子树的总权值和都为 \(1\)。

假设当前 \(u\) 所有子树的权值和都已经是 \(1\) 了，现在要合并到 \(u\)，那么就是 \(u\) 的点权 \(x\) 满足 \(x-儿子数=1\)，即 \(x-(\operatorname{deg}_u-1)=1\)，故 \(x=2-\operatorname{deg}_u\)。

(2). P2664 树上游戏

考虑转换为点对关系问题，对于下面的一棵树，\(1\) 是重心，只统计跨越重心的答案（即从 \(3\) 号子树内经过 \(1\)，通往 \(2\) 号子树内），\(2\) 号紫色点的贡献是多少？

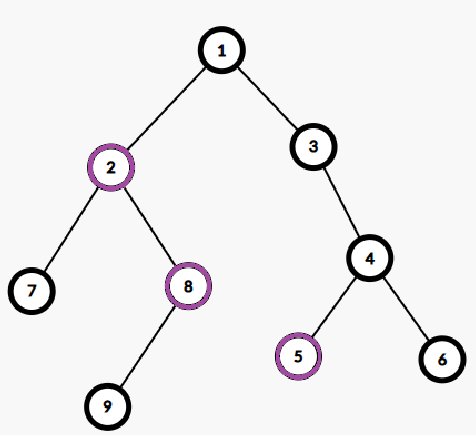
显然，对于每个 \(s(3,u)\)（\(u\) 是 \(2\) 子树内的点），答案都因为 \(2\) 是紫色增加了 \(1\)，所以 \(2\) 的贡献增加了 \(2\)。

那 \(8\) 有贡献吗？显然没有，它的贡献被 \(2\) 抢了。

那 \(s(5,u)\) 能吃到贡献吗？吃不到，因为它的贡献被 \(5\) 自己抢了。

也就是说，钦定一棵子树里的点作为出发的，其它子树内一种颜色只有一个节点有贡献，这个有贡献的节点是离重心最近的，于是就可以统计出每种颜色的贡献 \(s_i\)。直接先统计出所有子树的贡献，钦定一棵子树时把那个子树的贡献扣掉就好了。

对钦定子树进行统计时，先统计出总颜色贡献 \(sum\)，如果从重心到 \(x\) 的路径没有经过过 \(x\) 的颜色，那么往下走的时候 \(x\) 的颜色对应的贡献 \(s_{c_i}\) 也没了，用一个变量统计。

此外，这种统计方法还没有考虑从重心到钦定子树的节点 \(x\)，这中间的贡献，这显然是路径上不同颜色个数 \(\times\) 子树外大小。

接下来还有重心颜色的问题，还是暴力数出重心的连通块中，重心颜色仅出现一次的最大连通块大小，判断从重心走到 \(x\) 时有没有经过过重心颜色的节点，没有的话加上连通块大小即可。

（是的又是这张图……）

假设黑色节点其实是蓝色的，那么红色边上的节点都应该加上红色连通块大小（不包含蓝点）的贡献。

十分的复杂，但仔细想一下还是比较板的，就是分为三类讨论：贡献来自子树外，贡献来自子树内，贡献来自重心。

(3). P3714 [BJOI2017] 树的难题

这个就相对简单了，首先从重心出发往下的颜色序列的贡献是易于统计的，关键就在于跨越重心两端的边颜色是否相同。

其实，可以直接把每个节点的儿子按边颜色排序，颜色相同的一起处理即可。

接着还有距离问题，这就是一个区间查询，线段树维护即可。

总结，就是说开两个线段树，一个维护重心左右儿子颜色不同的情况，另一个维护重心左右儿子颜色相同的答案。

点分树

又叫“动态点分治”，实际上与点分治的关系只有建树方式相同，常用于带修树上问题。

1. 例题

还是拿一道例题来讲：P6329 【模板】点分树 | 震波。

什么是点分树呢，就是把重心串起来得到一棵新树。

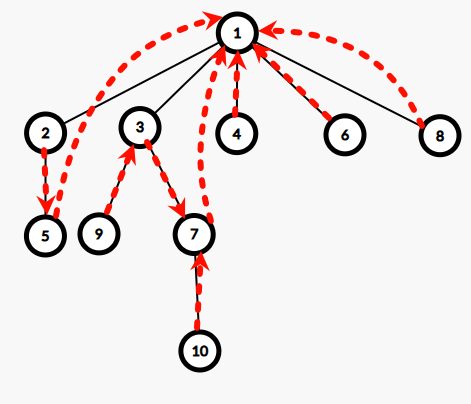
这样子，树高就变成了 \(\log\) 级别的，各种 \(?\times\) 树高的神秘暴力都能用了，但是有个问题，父子关系被完全打乱了，怎么办呢？我们可以换一种统计方式。

考虑只求子树内距离不超过 \(x\) 的点怎么做，用线段树下标表示距离，值表示总和即可，查询就是区间求和，但是由于还要包括上子树里的答案，每次更新时，把从这个点到根节点路径上的所有点，都更新上这个权值。

那么点分树上也是类似的，借用点分治的“跨越重心”思想，统计离 \(3\) 距离不超过 \(x\) 的点，每次都只查看绿色的点，只需要：

• 统计自己点分树子树内的答案。

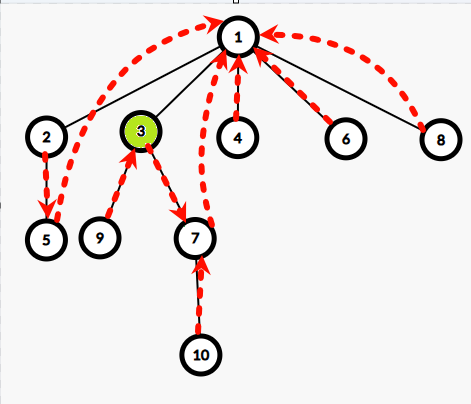
• 统计点分树父亲节点（黄色）中，扣掉自己这边子树（蓝色）内的答案。

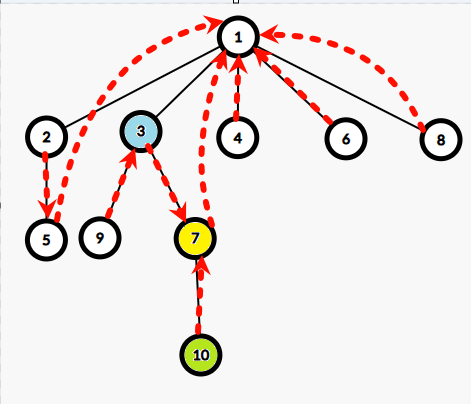
• 往上跳。

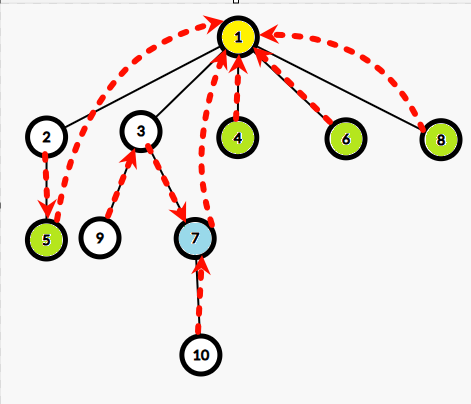
这样子，点分树算法的流程就明了了。

但是有个问题，点分树的父亲和儿子关系几乎微乎其微，不能用父亲的线段树减去儿子的线段树得到其它子树的答案，对于每个节点，只需要另外维护一个线段树，表示这个节点子树内和这个节点点分树上父亲的关系的即可。

核心代码（建树跑一遍点分治，把每个节点对应点分树上的父亲记录下来即可）。

t 是统计子树内的线段树，tf 是统计子树内和子树根点分树上父亲关系的线段树。

void update(int x, int v) {
    int u = x;
    while (u) {
        t.update(t.root[u], 0, n - 1, dis(u, x), v);
        if (dfa[u])
            tf.update(tf.root[u], 0, n - 1, dis(dfa[u], x), v);
        u = dfa[u];
    }
}
int query(int x, int v) {
    int u = x, pre = 0, ret = 0;
    while (u) {
        if (dis(u, x) <= v)
            ret += t.query(t.root[u], 0, n - 1, 0, v - dis(u, x)) - tf.query(tf.root[pre], 0, n - 1, 0, v - dis(u, x));
        pre = u, u = dfa[u];
    }
    return ret;
}

2. 刷题总结

(1). P4115 Qtree4

前置知识：可并堆

multiset 的常数太大了，有没有什么常数小的实现方法？

或者说写一个桶，满足以下功能：取最大值，添加一个数，删除其中任意一个数。

只需要写一个原桶，写一个删除桶，用优先队列实现，如果原桶的桶顶和删除桶的桶顶一致，就同时弹出。

struct DUI {
    priority_queue<int> q, d;
    int sz;
    void add(int x) {
        q.push(x), sz++;
    }
    void del(int x) {
        d.push(x), sz--;
    }
    void refresh() {
        while (!q.empty() and !d.empty() and q.top() == d.top())
            q.pop(), d.pop();
    }
    int top() {
        refresh();
        return q.top();
    }
};

先对每个节点维护一个可并堆 \(f_i\)，里面存放的是 \(i\) 点分树子树内所有白点，到 \(i\) 点分树父亲的距离。对于每个节点维护一个 \(mx_i\)，表示它的点分树儿子 \(v\) 中，\(\operatorname{top}(f_v)\) 的集合，如果 \(\operatorname{sz}(mx_i)\) 大于 \(1\)，那么它的前两大的和就有可能成为答案，丢进一个答案堆 \(ans\) 里即可。

每次更新白点黑点时，依次更新即可，代码有点恶臭但还算易懂。

(2). P3345 [ZJOI2015] 幻想乡战略游戏

考虑如果钦定补给点设在 \(u\)，如何用点分树的思路快速计算出总代价。显然对于从 \(u\) 到根，只需要记录出每个点的点分树子树代价和（当然要扣掉 \(u\) 这一边的贡献），再加上每个点的子树大小（扣）乘那个点到 \(u\) 的距离即可。

假设最优点是 \(x\)，当前点是 \(u\)，感性理解有 \(u\) 往 \(x\) 走，代价就会单调递减。

(3). P3241 [HNOI2015] 开店

套路还是一样的，无非就是怎么统计的问题，只需要存下子树内每个节点的年龄和距离，对子树内按年龄从小到大排个序，二分找到年龄区间前缀和优化做就完了。

记得加上点分树父亲到当前节点这段距离的贡献。