笛卡尔树 & 极值分治 笔记
本文原在 2024-07-25 10:02 发布于本人洛谷博客,于 2025-3 重构。
一、定义
以小根为例,每个节点由一个二元组 \((x_i,y_i)\) 组成,如果每个节点的 \(x\) 都小于它子树中所有节点的 \(x\)(小根堆),每个节点的 \(y\) 都大于其左子树所有节点的 \(y\) 而小于其右子树所有节点的 \(y\)(二叉搜索树),那么这就是一棵笛卡尔树。
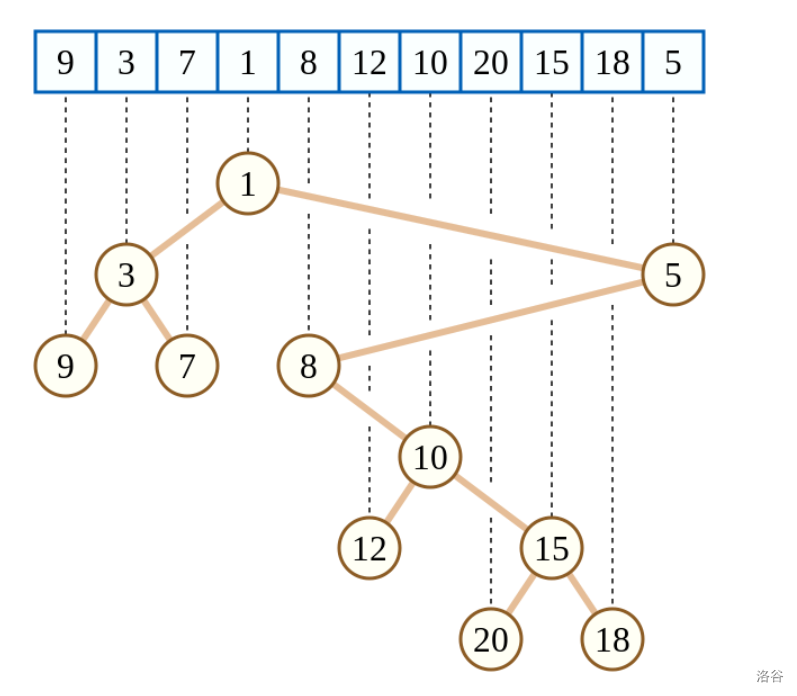
Treap 就是一种笛卡尔树,其中 \(rnd\) 是 \(x\),\(val\) 是 \(y\)。
二、建树
以模板题 P5854 【模板】笛卡尔树 为例。
这一题中节点权值 \(p_i\) 即为上面所说的 \(x_i\),节点编号 \(i\) 即为上面所说的 \(y_i\)。
维护一条从根节点一直走右儿子的链,存到栈里。
每次插入节点 \(u\) 时,从根节点往下寻找第一个比 \(x_u\)(\(u\) 节点按照小根堆性质排的权值)小的 \(x_v\),把 \(u\) 放到 \(v\) 的右儿子即可。
如果 \(v\) 已经有右儿子了,把 \(u\) 放在 \(v\) 的右儿子,把 \(v\) 的右儿子放在 \(u\) 的左儿子。
证明:
-
满足小根堆性质:\(v\) 是第一个 \(x\) 值比 \(u\) 小的点,\(v\) 原来的子树里的 \(x\) 值一定比 \(u\) 大。
-
满足二叉搜索树性质:程序是从 \(1\sim n\) 的顺序依次插入的,\(u\) 是最新插入的节点,编号一定比前面插入了的所有节点要大,因此它对于现有的任意一个节点都位于右子树,现有的任意一个节点若是它的子树,也一定是左子树。
证毕。
for (int i = 1; i <= n; i++) {
int tmp = top;
while (tmp and a[st[tmp]] > a[i])
tmp--;
if (tmp)
rs[st[tmp]] = i;
if (tmp < top)
ls[i] = st[tmp + 1];
st[++tmp] = i;
top = tmp;
}
三、RMQ
让 \(i\) 满足二叉搜索树性质,\(a_i\) 满足大根堆性质,直接从根往下递归找即可。
int query(int rt, int x, int y) {
if (x <= rt and rt <= y)
return a[rt];
if (x >= rt)
return query(rs[rt], x, y);
if (y < rt)
return query(ls[rt], x, y);
}
四、极值分治
其实只是借用了笛卡尔树的思想。
由于笛卡尔树是二叉树,所以如果把每一层的节点都看成“分割区间”,就相当于找到区间中的最大值然后分治左右两边。需要注意的是这样分治的区间并不能保证只有 \(O(\log n)\) 层。
找到最大值,对于最大值到区间左右两端的 \(\gcd\) 相同的,一起处理,由于 \(\gcd\) 每变化一次,至少变小一半,所以复杂度是可以保证的。
至于怎么找区间最大值和区间 \(\gcd\),使用 ST 表即可。
void solve(int l, int r) {
if (l > r)
return;
if (l == r) {
ans = (ans + 1ll * a[l] * a[l] % mod) % mod;
return;
}
int mid = qmx(l, r);
solve(l, mid - 1), solve(mid + 1, r);
v1.clear(), v2.clear();
for (int i = mid, j; i >= l; i = j - 1) {
int tmp = qg(i, mid);
j = findl(l, i, tmp);
v1.push_back({tmp, i - j + 1});
}
for (int i = mid, j; i <= r; i = j + 1) {
int tmp = qg(mid, i);
j = findr(i, r, tmp);
v2.push_back({tmp, j - i + 1});
}
for (auto [x1, l1] : v1)
for (auto [x2, l2] : v2)
ans = (ans + 1ll * mygcd(x1, x2) * a[mid] % mod * l1 % mod * l2 % mod) % mod;
}
五、刷题总结
1. P6453 [COCI2008-2009#4] PERIODNI
以样例为例,从下往上看,按如图方式划分成若干矩形。
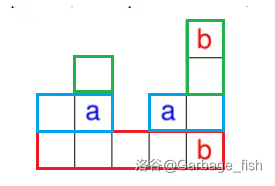
也就是从下往上看,把当前矩形扩展到最大,然后再把左上方和右上方划分。
而对于左右界为 \([l,r]\) 的矩形,显然上界是 \(\min_{i=l}^r h_i\),所以可以用 \(i\) 来代表这个矩形。
因此以 \(h_i\) 为小根堆权值构建笛卡尔树。
设 \(f(u,k)\) 表示 \(u\) 节点代表的矩形及它上面的矩形,一共放 \(k\) 个数字的方案数。
遍历每个节点 \(O(n)\),对于下面那一串,每个节点状态数 \(O(k)\),转移 \(O(k^2)\),TLE。
考虑优化转移。
设
则
遍历每个节点 \(O(n)\),每个节点求 \(g\) \(O(k^2)\),每个节点状态数 \(O(k)\),转移 \(O(k)\),总时间复杂度 \(O(nk^2)\),可过。
#include <bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
const int N = 510, mod = 1e9 + 7;
int n, k, a[N], f[N][N], g[N][N], sz[N];
int ls[N], rs[N], st[N], top;
int fac[1000010], invf[1000010];
int inv(int x) {
int ret = 1;
for(int i = mod - 2; i; i >>= 1, x = x * x % mod)
if (i & 1)
ret = ret * x % mod;
return ret;
}
void get_fac(int x) {
fac[0] = invf[0] = 1;
for (int i = 1; i <= x; i++) {
fac[i] = fac[i - 1] * i % mod;
invf[i] = inv(fac[i]);
}
}
int A(int n, int m) {
if (n < m)
return 0;
return fac[n] * invf[n - m] % mod;
}
void build() {
for (int i = 1; i <= n; i++) {
int tmp = top;
while (tmp and a[st[tmp]] > a[i])
tmp--;
if (tmp)
rs[st[tmp]] = i;
if (tmp < top)
ls[i] = st[tmp + 1];
st[++tmp] = i;
top = tmp;
}
}
void get_sz(int u) {
if (ls[u])
get_sz(ls[u]);
if (rs[u])
get_sz(rs[u]);
sz[u] = sz[ls[u]] + sz[rs[u]] + 1;
}
void dfs(int u, int low) {
int up = a[u] - low;
if (!ls[u] and !rs[u]) {
f[u][0] = 1;
for (int i = 1; i <= k; i++)
f[u][i] = A(sz[u], i) * A(up, i) % mod * invf[i] % mod;
return;
}
if (ls[u])
dfs(ls[u], a[u]);
if (rs[u])
dfs(rs[u], a[u]);
g[u][0] = 1;
for (int i = 1; i <= k; i++)
for (int j = 0; j <= i; j++)
g[u][i] = (g[u][i] + f[ls[u]][j] * f[rs[u]][i - j] % mod) % mod;
f[u][0] = 1;
for (int i = 1; i <= k; i++)
for (int j = 0; j <= i; j++)
f[u][i] = (f[u][i] + g[u][j] * A(up, i - j) % mod * A(sz[u] - j, i - j) % mod * invf[i - j] % mod) % mod;
}
signed main() {
IOS;
cin >> n >> k;
get_fac(1e6);
for (int i = 1, x; i <= n; i++)
cin >> a[i];
build();
get_sz(st[1]);
f[0][0] = 1;
dfs(st[1], 0);
cout << f[st[1]][k];
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号