2-SAT 笔记

本文原在 2024-07-22 16:34 发布于本人洛谷博客。

一、定义

\(\vee\) 是或，\(\wedge\) 是与。

2-SAT 解决形如

\[(x_1 \vee \neg x_2) \wedge(\neg x_1 \vee x_3)\wedge... \]

的问题。

二、解决方法

我们把一个点 \(x\) 拆成两个状态：\(x_0\) 表示 \(x=0\)，\(x_1\) 表示 \(x=1\)。在题目给出的限制中，显然这些状态是可以互相推理的。

1. \(x\vee y\)

\(x_0\Rightarrow y_1\)，\(y_0\Rightarrow x_1\)。

2. \(\neg x \vee y\)

\(x_1\Rightarrow y_1\)，\(y_0\Rightarrow x_0\)。

3. \(x \vee \neg y\)

\(x_0\Rightarrow y_0\)，\(y_1\Rightarrow x_1\)。

4. \(\neg x \vee \neg y\)

\(x_1\Rightarrow y_0\)，\(y_1\Rightarrow x_0\)。

如果用 \(a=1\) 表示式子中要求 \(x\) 为真，\(a=0\) 表示式子中要求 \(x\) 为假，\(b\) 表示式子中要求 \(y\) 的状况，那么观察可以得到：

\(x_{a\oplus 1}\Rightarrow y_{b\wedge 1}\)，\(y_{b\oplus 1}\Rightarrow x_{a\wedge 1}\)。

我们根据推理情况建有向图，跑强连通分量，如果存在 \(x_0\) 和 \(x_1\) 在同一强连通分量内，则说明无解。

当 \(x_1\) 所在的强连通分量的拓扑序在 \(x_0\) 所在的强连通分量的拓扑序之后取 \(x\) 为真，Kosaraju 算法按拓扑序排好的，Tarjan 算法则是反着的拓扑序，要将 \(scc_{x_1}>scc_{x_0}\) 改为 \(scc_{x_1}<scc_{x_0}\)。

cin >> n >> m;
for (int i = 1, x, a, y, b; i <= m; i++) {
    cin >> x >> a >> y >> b;
    add(x + n * (a & 1), y + n * (b ^ 1));
    add(y + n * (b & 1), x + n * (a ^ 1));
}
kosaraju();
for (int i = 1; i <= n; i++)
    if (scc[i] == scc[i + n]) {
        cout << "IMPOSSIBLE";
        return 0;
    }
cout << "POSSIBLE\n";
for (int i = 1; i <= n; i++)
    cout << (scc[i] > scc[i + n]) << " ";

三、建图优化

如果有这么一张 \(n^2\) 的图：

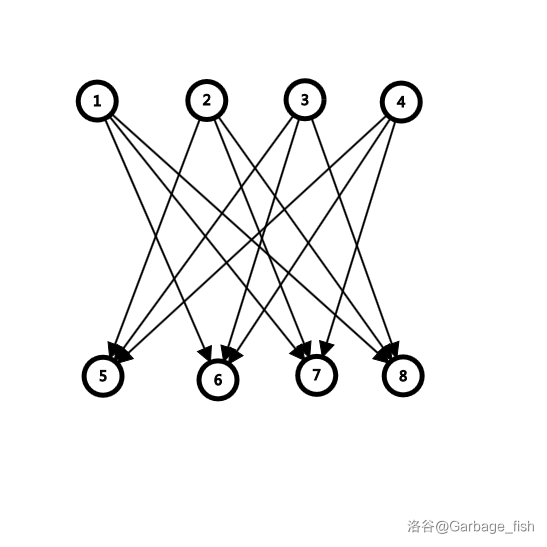
举 \(2\) 号点为例，发现它要这样连边：

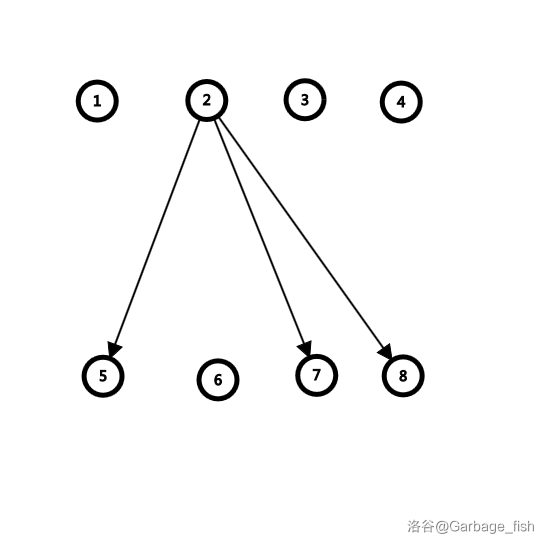
所以弄两班公交车，一班向右走，一班向左走：

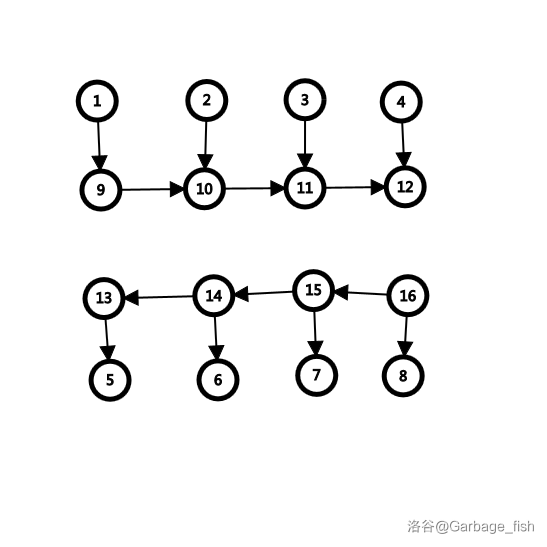
因为 \(2\) 号点要去 \(5\) 号点及其左边的点，所以他在 \(13\) 号点上向左走的公交车；\(7\) 号点应该要被 \(2\) 号点及其左边的点去，\(8\) 号点应该被 \(3\) 号点及其左边的点去，所以将 \(2\)，\(3\) 号点对应的公交站 \(10\)，\(11\) 号点和 \(7\)，\(8\) 号点连边。

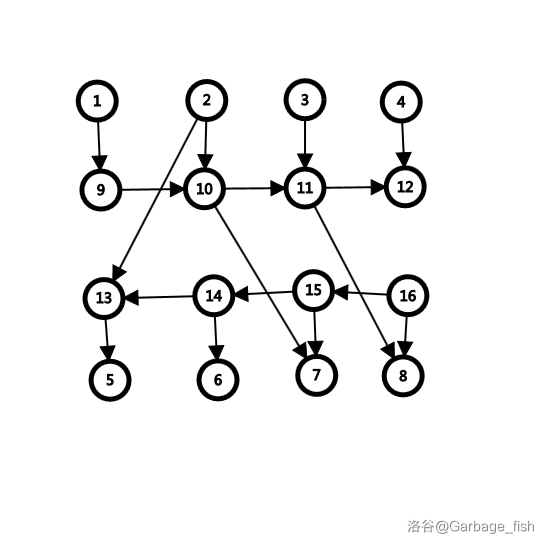
剩下的点同理：

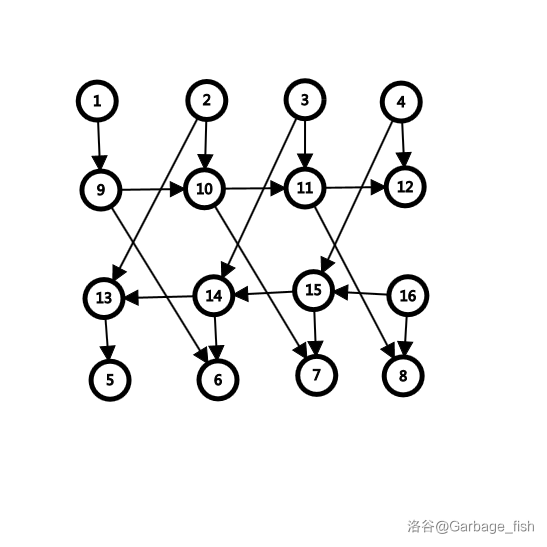
我们成功把边数优化到 \(O(n)\) 级别的（由于常数是 \(6\)，上图 \(n=4\)，所以看起来像是还更多边了，实则当 \(n\) 有一定大小时并不是）。