Splay 笔记

本文原在 2024-07-15 15:27 发布于本人洛谷博客。

一、基本概念

1. 二叉搜索树

一棵每个节点的左子树的权值都比那个节点要小，右子树的权值都比那个节点要大的二叉树。

二、Splay 的操作

1. 建点

需要统计这个点的权值 \(val\)，子树大小 \(sz\)，这个点的权值的“个数” \(cnt\)，左儿子、右儿子、父节点编号 \(ls,rs,fa\)。

struct node {
	int val, sz, cnt, ls, rs, fa;
} tree[N];
int rt, gid;
int newnode(int val) {
	tree[++gid] = {val, 1, 1, 0, 0, 0};
	return gid;
}

2. 初始化

插入两个哨兵节点 \(-10^9\) 和 \(10^9\) 防止操作越界。

void init_() {
	gid = 0;
	int p = newnode(oo);
	rt = newnode(-oo);
	rs(rt) = p;
	fa(p) = rt;
	tree[rt].sz = 2;
}

3. 维护子树 \(sz\) 大小

就是线段树的 push_up。

void push_up(int x) {
	tree[x].sz = tree[x].cnt;
	if (ls(x) != 0) tree[x].sz += tree[ls(x)].sz;
	if (rs(x) != 0) tree[x].sz += tree[rs(x)].sz;
}

4. 旋转

以左旋（zag，右旋称为 zig）\(x\) 为例：

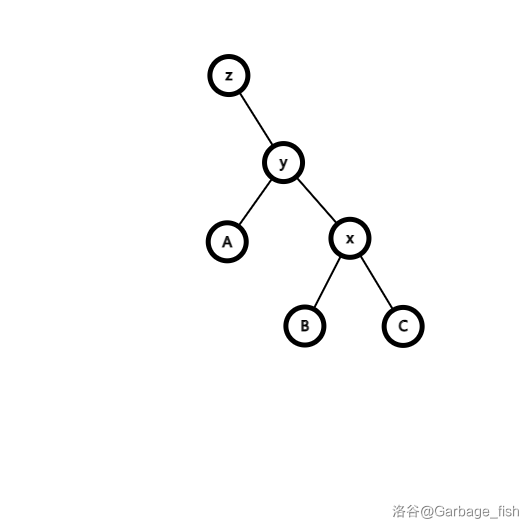
• 断边，旋转只与他的父节点有关。

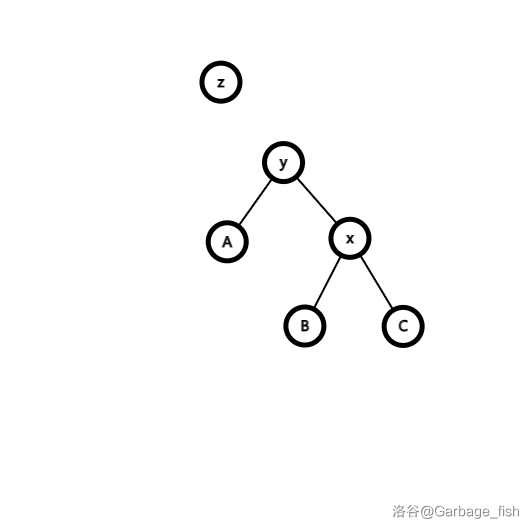
• 向左旋转，也就是把 \(x\) 向左拿上来，\(y\) 向左放下去

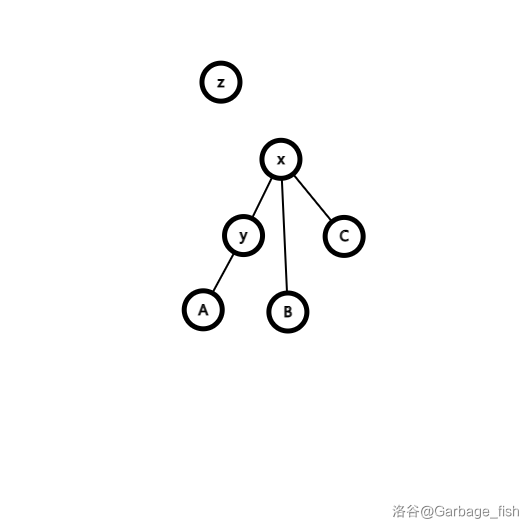
• 这时 \(x\) 有三棵子树，\(y\) 只有一棵。由二叉搜索树的定义，\(y<B<x\)，所以把 \(B\) 放到 \(y\) 的右子树。

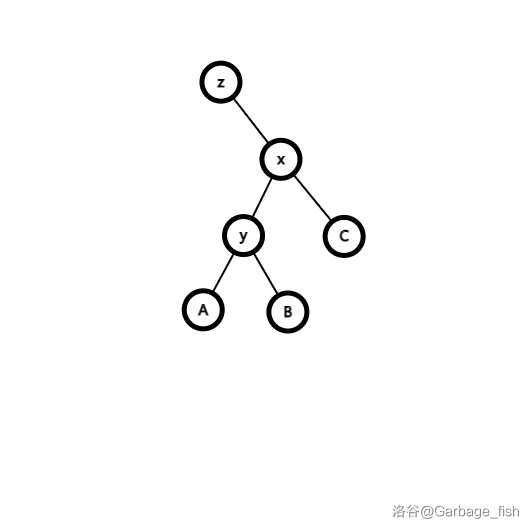
右旋同理。

void zag(int x) {
	int y = fa(x), z = fa(y);
	rs(y) = ls(x);
	if (ls(x) != 0) fa(ls(x)) = y;
	push_up(y);
	ls(x) = y;
	fa(y) = x;
	push_up(x);
	fa(x) = z;
	if (z != 0) {
		if (ls(z) == y) ls(z) = x;
		else rs(z) = x;
	}
}
void zig(int x) {
	int y = fa(x), z = fa(y);
	ls(y) = rs(x);
	if (rs(x) != 0) fa(rs(x)) = y;
	push_up(y);
	rs(x) = y;
	fa(y) = x;
	push_up(x);
	fa(x) = z;
	if (z != 0) {
		if (ls(z) == y) ls(z) = x;
		else rs(z) = x;
	}
}

5. \(Splay(x, T)\)

表示将 \(s\) 旋转至 \(T\) 的下方。

每次旋转只有以下六种情况。

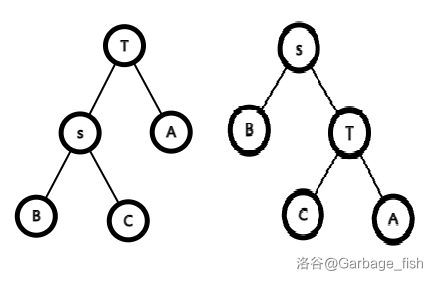
(1). 一步到位：\(s\) 是 \(T\) 的儿子。

左儿子就 \(zig(s)\)，右儿子就 \(zag(s)\)。

以左儿子为例：

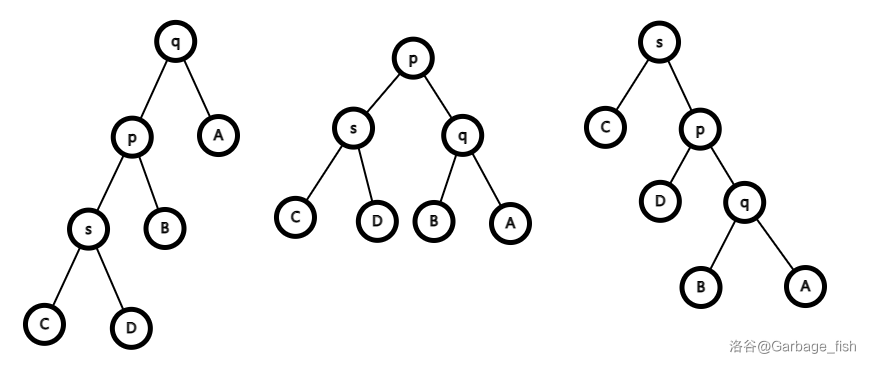
(2). 在路上：\(s\) 是 \(p\) 的儿子，\(p\) 是 \(q\) 的儿子，\(s,p\) 在 \(p,q\) 同侧。

同为左侧就 \(zig(p)\to zig(s)\)，同为右侧就 \(zag(p)\to zag(s)\)。

以同为左侧为例：

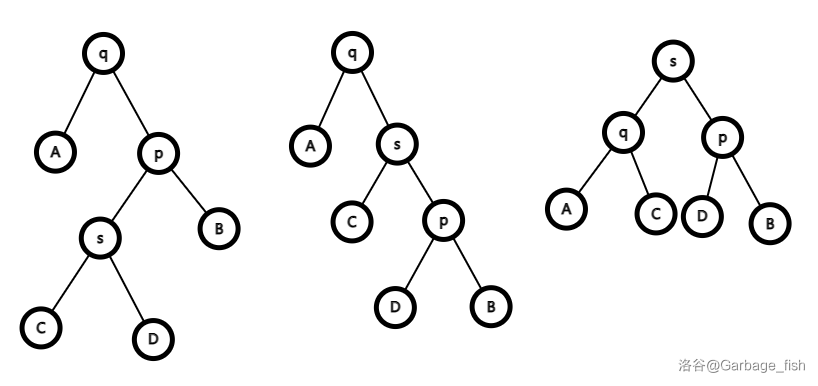
(3). (2) 的情况，但是 \(s,p\) 在 \(p,q\) 异侧。

\(s\) 在 \(p\) 左侧，\(p\) 在 \(q\) 右侧就 \(zig(s)\to zag(s)\)；反之就 \(zag(s)\to zig(s)\)。

以 \(s\) 在 \(p\) 左侧为例：

多次使用以上操作，我们就可以完成 \(Splay\) 操作。

void splay(int x, int T) {
	while(fa(x) != T) {
		int y = fa(x), z = fa(y);
		if (z == T) {
			if (x == ls(y)) zig(x);
			else zag(x);
		} else {
			bool xl = (x == ls(y)), yl = (y == ls(z));
			if (xl and yl) zig(y), zig(x);
			else if (!xl and !yl) zag(y), zag(x);
			else if (xl and !yl) zig(x), zag(x);
			else zag(x), zig(x);
		}
	}
	if (fa(x) == 0) rt = x;
}

6. 求前驱/后继

指小于（或大于）指定数 \(val\) 的最大（或最小）数。

以前驱为例。我们直接从根遍历二叉树，如果当前所在节点小于 \(val\)，那么就记它为最优答案，遍历它的右子树，否则就不更新最优答案，遍历它的左子树。

int pre(int p, int val, int best) {
	if (p == 0) return best;
	if (val > tree[p].val) return pre(rs(p), val, p);
	else return pre(ls(p), val, best);
}
int nxt(int p, int val, int best) {
	if (p == 0) return best;
	if (val < tree[p].val) return nxt(ls(p), val, p);
	else return nxt(rs(p), val, best);
}

7. 插入操作

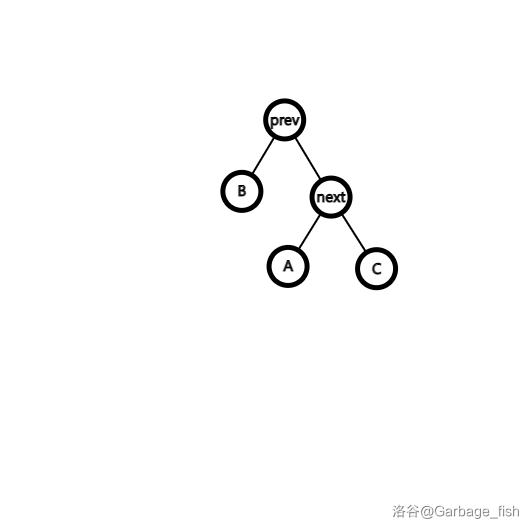
将当前插入数 \(val\) 的前驱 \(prev\) 旋转到整棵树的根，后继 \(next\) 旋转到根 \(prev\) 的右子树，那么 \(A\) 的这个地方绝对是空的（或者是 \(val\) 本身）。

简单证明：

• \(prev\) 是比 \(val\) 小的最大数，所以比 \(val\) 小的其他数都比 \(prev\) 小，位于 \(B\) 的这个地方。

• \(next\) 是比 \(val\) 大的最小数，所以比 \(val\) 大的其他数都比 \(next\) 大，位于 \(C\) 的这个地方。

• 所以比 \(val\) 小或者比 \(val\) 大的任何数都不在 \(A\) 这个位置。

• 证毕。

如果 \(next\) 的左子树为空，新增一个节点，否则就直接给那个节点的 \(cnt\)（统计这个节点有多少“个”）加一就行了。

int insert(int p, int val) {
	int prev = pre(rt, val, 0);
	splay(prev, 0);
	int next = nxt(rt, val, 0);
	splay(next, prev);
	if(ls(next) != 0) tree[ls(next)].cnt++, tree[ls(next)].sz++;
	else {
		ls(next) = newnode(val);
		fa(ls(next)) = next;
	}
	push_up(next);
	push_up(rt);
	return ls(next);
}

8. 删除

同插入理。

void remove(int p, int val) {
	if (p == 0) return;
	int prev = pre(rt, val, 0);
	splay(prev, 0);
	int next = nxt(rt, val, 0);
	splay(next, prev);
	if (ls(next) != 0 and tree[ls(next)].val == val) {
		if (tree[ls(next)].cnt > 1) tree[ls(next)].cnt--, push_up(ls(next));
		else ls(next) = 0;
		push_up(next);
		push_up(rt);
	}
}

9. 求当前数排名

从小到大的排名。

把他的前驱移到左子树，这样比他小的数都在它的左子树，所以就是左边整棵子树的大小加一（但由于哨兵的存在，最后调用要减回去一）。

int get_rank(int p, int val) {
	int prev = pre(rt, val, 0);
	if (prev == 0) return 1;
	splay(prev, 0);
	int next = nxt(rt, val, 0);
	splay(next, prev);
	return tree[ls(prev)].sz + tree[prev].cnt + 1;
}

10. 查找某一排名的树

看一下左边子树的大小有没有超过当前排名，超过了就往左子树找，还没达到就往右子树找。往右子树找要减去左边子树的大小。

int findk(int p, int k) {
	int lsz = 0;
	if (ls(p) != 0) lsz = tree[ls(p)].sz;
	if (k <= lsz) return findk(ls(p), k);
	else if (k <= lsz + tree[p].cnt) return p;
	else return findk(rs(p), k - lsz - tree[p].cnt);
}