CDQ 分治 笔记

本文原在 2024-07-15 08:15 发布于本人洛谷博客。

一、二维偏序

给定一个序列，求每个 \(j\) 满足 \(i< j, a_i\le a_j, b_i\le b_j\) 的个数。

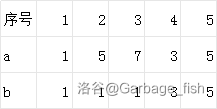
先将序列按 \(a\) 为第一关键字，按 \(b\) 为第二关键字排序。

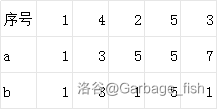
然后分成 \([ls,mid]\)（\([1,3]\)）和 \([mid,rs]\)（\([4,5]\)）分治每一个区间。

先计算小区间的答案再计算大区间的答案，计算答案以 \([1,5]\) 区间为例。因为已经按 \(a\) 排过序了，所以右边这个区间的 \(a\) 绝对全部大于等于左边区间的 \(a\)，接下来处理 \(b\) 就行了。

将两个分别按 \(b\) 排序，然后双指针即可找右边区间比左边区间 \(b\) 大的了。

如图，\(i\) 找到第一个比 \(j\) 的 \(b\) 大的，这说明 \([ls, i-1]\) 的都是满足我们的要求的。

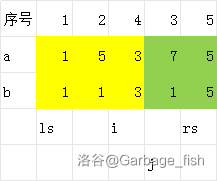
因为 \(b\) 已经有序，所以 \(i_{j+1} \ge i_j\)。

void cdq(int ls, int rs) {
	if (ls >= rs)
		return;
	int mid = (ls + rs) >> 1;
	cdq(ls, mid);
	cdq(mid + 1, rs);
	sort(a + ls, a + mid + 1, cmp2);
	sort(a + mid + 1, a + rs + 1, cmp2);
	for (int i = ls, j = mid + 1; j <= rs; j++) {
		while (i <= mid and a[i].b <= a[j].b) i++;
		a[j].cnt += i - ls;
	}
}

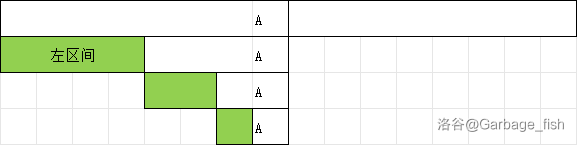
为什么不会算重？如下图，\(A,B\) 区间计算完之后合并成 \(D\) 区间，如果 \(D\) 区间和 \(C\) 一起处理，那 \(B\) 中的数也不会和 \(A\) 再计算一次，因为都在 \(D\) 里面。如果和 \(E\) 一起处理，那 \(B\) 区间的数是被用于计算的数，也不会多算。

为什么不会算漏？观察下图我们可以发现 \(A\) 肯定能和前面的所有数字进行计算。

二、三维偏序

\(a\) 和 \(b\) 都解决了，再加一个 \(c\) 就用树状数组处理即可（用树状数组存左边符合 \(a,b\) 要求的 \(c\)，右边求答案求树状数组中符合 \(c\) 的条件的即可）。

最后记得将树状数组还原。

void cdq(int ls, int rs) {
	if (ls >= rs)
		return;
	int mid = (ls + rs) >> 1;
	cdq(ls, mid);
	cdq(mid + 1, rs);
	sort(a + ls, a + mid + 1, cmp2);
	sort(a + mid + 1, a + rs + 1, cmp2);
	int i = ls, j = mid + 1;
	for (; j <= rs; j++) {
		while (i <= mid and a[i].b <= a[j].b) {
			update(a[i].c, a[i].cnt);
			i++;
		}
		a[j].ans += query(a[j].c);
	}
	i--;
	for (; i >= ls; i--)
		update(a[i].c, -a[i].cnt);
}