最大子矩形笔记

ee0f89de-4886-4f8e-848e-62b47773e706

一、最大子矩阵是什么

在一个给定的矩形网格中有一些障碍点，要找出网格内部不包含任何障碍点，且边界与坐标轴平行的最大子矩形。

二、概念解释

1. 有效子矩形

内部不包含任何障碍点且边界与坐标轴平行的子矩形。

2. 极大有效子矩形

一个有效子矩形，如果不存在包含它且比它大的有效子矩形，就称这个有效子矩形为极大有效子矩形，简称极大子矩形。

三、定理

1. 一个最大子矩形一定是一个极大子矩形。

如果这个最大子矩形不是极大子矩形，那么还有包含它且比它大的有效子矩形，与它是最大子矩形矛盾。

2. 一个极大子矩形四边一定不能继续向外扩展。

这是显而易见的。

四、实现方法

1. 悬线法

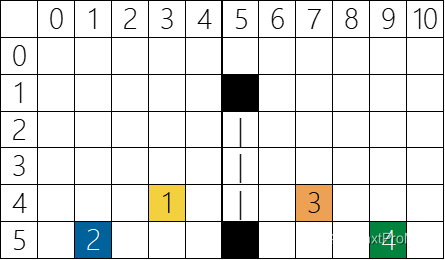
如上图所示，两个黑色点之间的即为一条悬线，那么我们只需要枚举这一条悬线能到达的左边界与右边界，即可得到一个极大子矩阵的面积。

直接枚举每两个点之间是否可以连成悬线是不可行的，所以不如用 $3$ 个数组 $h,l,r$，分别表示以当前点为悬线下端的悬线的长度，该悬线能往左到达的最远点与往右能到达的最远点。然后使用 $(r_{i,j}-l_{i,j})\times h_{i,j}$ 得到面积。

(1). $h_{i,j}$ 的状态转移方程。

首先初始时，每个点都可以视为一个悬线，即 $h_{i,j}=1$。

不难发现，如果这个点是一个障碍点，那么 $h_{i,j}$ 的高度即位 $0$，否则即可以把这个点视为上方悬线经过的点，那么 $h_{i,j}=h_{i-1,j}+1$。假设 $a_{i,j}=1$ 表示 $(i,j)$ 为一个障碍点，那么有：

$$ h_{i,j}=\left\{\begin{matrix}0 & a_{i,j}=1\\ h_{i-1,j}+1 & a_{i,j}\ne1 \end{matrix}\right. $$

(2). $l_{i,j}$ 与 $r_{i,j}$ 的状态转移方程。

首先初始时，将每个点都视为一根悬线。由于不知道他能往左或往右走到哪里，所以赋初值为 $l_{i,j}=1,r_{i,j}=1$。

然后先看每个点往左和往右最多能走到哪里，即：

$$l_{i,j}=l_{i,j-1}(a_{i,j}\ne1,a_{i,j-1}\ne1)$$

$$r_{i,j}=r_{i,j+1}(a_{i,j}\ne1,a_{i,j-1}\ne1)$$

最后再处理每根长度大于 $1$ 的悬线的情况。拿上图往左边来举例，尽管坐标为 $(5,5)$ 的点能往左走到 $2$ 号点，但是因为他上方的点 $(4,5)$ 只能走到 $1$ 号点，所以这条悬线也只能走到 $1$ 号点的位置。由于这是往左走，所以越靠近悬线 $y$ 轴上的值越大，因此取 $\max$。

$$l_{i,j}=\max(l_{i,j},l_{i-1,j})$$

同理可得，$r_{i,j}$ 的值也受到 $r_{i-1,j}$ 的影响，但这是往右走，所以取 $\min$。

$$r_{i,j}=\min(r_{i,j},r_{i-1,j})$$

最后算出来每个极大子矩阵的面积，输出答案即可，时间复杂度为 $O(nm)$。

(3). 例题

平台	网址
洛谷	https://www.luogu.com.cn/problem/P4147

AC Code:

#include <bits/stdc++.h>
#define int long long 
using namespace std;
void fread(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
}
const int N=1e3+10,oo=0x7fffffff;
int n,m,cnt,a[N][N],h[N][N],l[N][N],r[N][N],ans;
signed main(){
    fread();
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            char c;
            cin>>c;
            if(c=='R'){
                a[i][j]=1;
            }
            else cnt++;
            l[i][j]=r[i][j]=j;
            h[i][j]=1;
        }
    }
    if(!cnt){
        cout<<0;
        return 0;
    }
    for(int i=1;i<=n;i++){
        for(int j=2;j<=m;j++){
            if(!a[i][j] and !a[i][j-1]){
                l[i][j]=l[i][j-1];
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=m-1;j>=1;j--){
            if(!a[i][j] and !a[i][j+1]){
                r[i][j]=r[i][j+1];
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(i>1 and !a[i][j] and !a[i-1][j]){
                l[i][j]=max(l[i][j],l[i-1][j]);
                r[i][j]=min(r[i][j],r[i-1][j]);
                h[i][j]=h[i-1][j]+1;
            }
            ans=max(ans,(r[i][j]-l[i][j]+1)*h[i][j]);
        }
    }
    cout<<ans*3;
    return 0;
}

2. 枚举法

(1). 步骤

此枚举非彼枚举，时间复杂度可达到 $O(s^2)$，其中 $s$ 表示障碍点的个数。

这个枚举法主要步骤有以下几步：

将障碍点按 $x$ 坐标从小到大排序。
枚举每个障碍点 $(x_1,y_1)$ 作为起点。
用 $up$ 表示当前极大子矩阵 $y$ 坐标的上界，用 $down$ 表示当前极大子矩阵 $y$ 坐标的下界。
往后枚举每一个障碍点 $(x_2,y_2)$，记录以 $up-down$ 为长，$x_2-x_1$ 为宽的矩形的面积，并更新 $down$ 与 $up$。
将障碍点按 $x$ 坐标从大到小排序，仿照第 $2,3,4$ 步再做一次二重循环。
将障碍点按 $y$ 坐标从小到大排序，枚举相邻两个障碍点之间的矩形的面积。

图解：

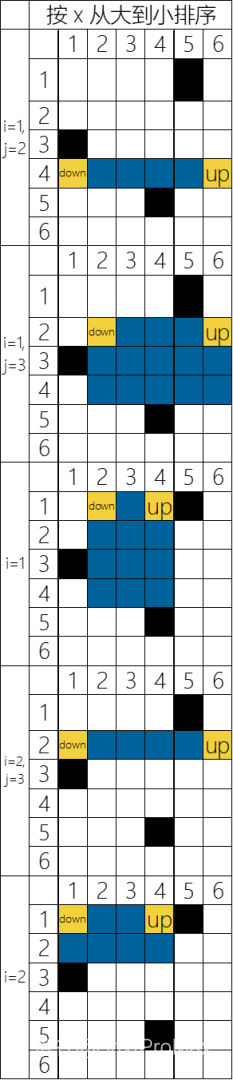
(2). 例题

平台	网址
洛谷	https://www.luogu.com.cn/problem/P1578