基环树

这几天学了好多新东西呢……但由于我太懒了，只能一点一点写了。

环

环是什么呢，不要怀疑自己，就是一个圆形，英文是\(circle\)
就比如下面这个丑陋的玩意：

的确很丑陋

基环树

一、定义

那么基环树是神马玩意呢？欸对，真聪明，就是一棵带了环的树话说那不就不是树了嘛
同时，他一定一定有\(n\)个点和
\(n\)条边。（当然，由\(n\)个点和\(n\)条边组成的同样可能是“基环树森林”，也就是由多棵基环树组成的森林）

下面这个丑陋的就是基环树：

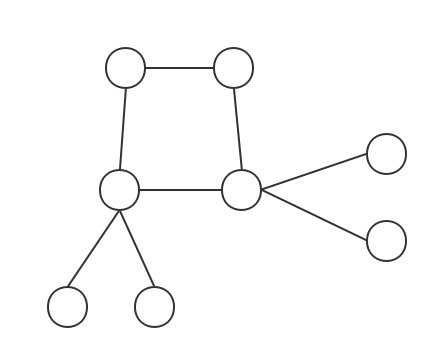
当然他的全名叫做无向基环树，就表示他没有方向。

他还有几个兄弟，长得同样丑陋，最经典的比如说内向基环树，顾名思义，就是很内向的基环树，就是下面这个丑陋的东西：

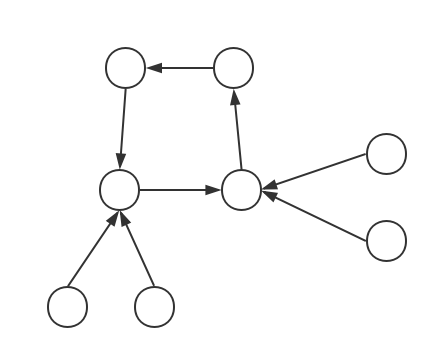
看上去就很内向当然，内向基环树必须满足每个点只有一条出边

有内向的自然就也有外向的，比如下面这个仍然丑陋的东西：

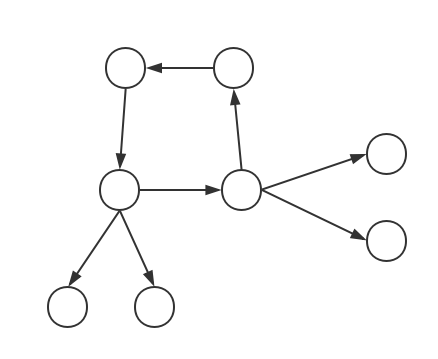
看上去就很外向同样，外向基环树同样需要满足一个条件：每个点只有一条入边

二、找环

基环树比树特殊就特殊在多了一个环，那么去寻找这个环就是解决问题的重中之重，找到这个环就可以把问题分解成两个部分来解决：

• 树上问题
• 环上问题

那么问题来了，怎么找环呢？

一般地，分为几种方法：经典的比如说\(tarjan\),拓扑排序或者使用并查集找环。

1.拓扑排序找环

自认为是最简单易懂的一种找环方式。

基本思路：每次将入度为1的点加入队列，并将与之相连的点入度减1，直到最后找不到入度为1的后就结束，剩下的就是环。
代码如下：

void topsort()
{
	int l = 0, r = 0;
	for (int i = 1; i <= n; i++)
	{
		if (in[i] == 1)q[++r] = i;
	}
	while (l < r)
	{
		int now = q[++l];
		for (int i = is[now]; i; i = a[i].next)
		{
			int y = a[i].to;
			if (in[y] > 1)
			{
				in[y]--;
				if (in[y] == 1)q[++r] = y;
			}
		}
	}
 } 

2.\(tarjan\)找环

到目前为止都不理解，求大佬讲解思路。

代码如下：

void tarjan(int u, int pre)
{
	dfn[u] = low[u] = ++cnt;
	s.push(u);
	vis[u] = 1;
	for (int i = 0; i < e[u].size(); i++)
	{
		int v = e[u][i];
		if (v == pre)continue;
		if (!dfn[v])
		{
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
		}
		if (vis[v] == 1)low[u] = min(low[u], dfn[v]);
	}
	if (dfn[u] == low[u])
	{
		vector<int> path;
		while (1)
		{
			int t = s.top();
			s.pop();
			path.push_back(t);
			vis[t] = 0;
			if (t == u)break;
		}
		if (path.size() > 1)
		{
			ans = path;
			return;
		}
	}
}

3.并查集找环

到目前为止都不理解，求大佬讲解思路。

代码还没有

三、基环树问题的求解方法

• 断环法：每次断开环上的一条边跑一遍答案，然后根据题目求解
• 二次\(dp\)：先处理子树，再处理环上，如环形\(dp\)一样将一条边强行断开处理一遍，然后强行连上再处理一遍

四、练习题

1.[IOI2008]Islands
2.[ZJOI2008]骑士
3.[NOIP2018]旅行 加强版
4.创世纪
5.Freda的传呼机
6.[POI2012]Rendezvous
7.[NOIP2018提高组]旅行
8.CF835F Roads in the Kingdom