Splay平衡树

一、二叉搜索树(\(BST\))

由于\(Splay\)就是一种\(BST\)，所以先来说说\(BST\)是什么。

定义：

\(BST\)其实就是一棵树，不一定为满二叉树， 但必定遵循左子树 < 根 < 右子树。

操作

基础操作都十分简单：

• 添加元素：每次与当前所在节点比较大小，小就往左走，大就往右走，直到找到一个空位就停下来。
• 查询元素：和根比较大小，小就往左，大就往右，找到为止。
• 删除元素：先查询，找到之后总节点数-1，然后调整（把子树调整到当前位置，再按照左子树 < 根 < 右子树的规则调整）即可

二、\(Splay\)

开启话痨模式：
不知道\(Splay\)是啥，，你也要知道平衡树是啥。
平衡树是一个神奇的数据结构，
对于任意一个节点，左儿子的值比它小，右儿子的值比它大。
并且任意一棵子树单独拎出来也是一棵平衡树。
就像这样：

上面这个丑陋的东西就是一棵平衡树，他现在很平衡，是一棵满二叉树，高度正好是\(logn\)。
但是……
如果这个丑陋的东西极端一点，他就会变成这样：

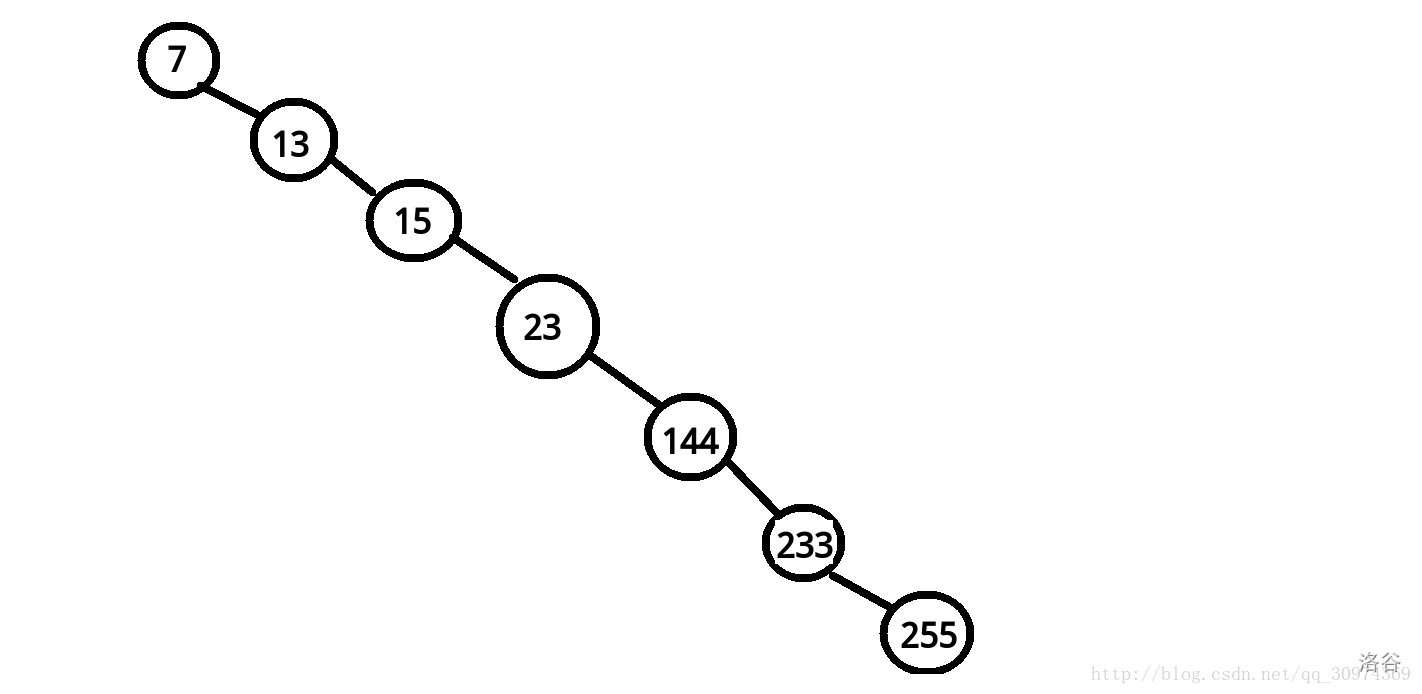
现在看起来，这个东西一点都不平衡……
二叉树退化成了一条链
如果要查询的话，，，最坏情况下就变成了\(O(n)\)
这就很尴尬了。
于是有个大佬叫做\(Tarjan\)发明了\(Splay\)来保持平衡树平衡的外形……

三、代码

施工中

#include <bits/stdc++.h>
using namespace std;

struct tree
{
	int ch[2];
	int ff;
	int val; 
}t[1000001]; 

//t是树上节点的结构
//ch数组表示左右儿子 
//ch[0]是左儿子 
//ch[1]是右儿子 
//ff是父节点
//val是当前位置存储的值 

int root;//平衡树的根 

inline void rotate(int x)
{
	/*
	//思路
	总结一下：
	1.X变到原来Y的位置
	2.Y变成了 X原来在Y的 相对的那个儿子
	3.Y的非X的儿子不变 X的 X原来在Y的 那个儿子不变
	4.X的 X原来在Y的 相对的 那个儿子 变成了 Y原来是X的那个儿子
	*/
	int y = t[x].ff;//X的父亲 
	int z = t[y].ff;//X的爷爷
	int k = ty.ch[1] == x;//X是Y的左儿子还是右儿子 
	t[z].ch[t[z].ch[1] == y] = x;//Z的原来的Y的位置变成X
	/*
	注：t[y].ch[1]是y的右儿子，
	如果x是右儿子，
	那么这个式子是1，
	否则是0，
	也正好对应着左右儿子 
	*/ 
	t[x].ff = z;//X的父亲变成Z
	t[y].ch[k] = t[x].ch[k ^ 1];//X的与X原来在Y的相对的那个儿子变成Y的儿子
	t[t[x]/ch[k ^ 1]].ff = y;//更新父节点
	t[x].ch[k ^ 1] = y;//X的与X原来相对位置的儿子变成Y
	t[y].ff = x;//更新父节点 
}
/* 
注：同样的k。表示相对的儿子，左儿子0 ^ 1 = 1 右儿子1 ^ 1 = 0 
*/ 

inline void splay(int x, int goal)//将X旋转为goal的儿子，如果goal = 0则旋转到根
{
	/*
	//思路
	如果要把X旋转到Z的位置
	归类一下，其实只有两种：
	第一种，X和Y分别是Y和Z的同一个儿子
	第二种，X和Y分别是Y和Z不同的儿子
	对于情况一，就要考虑先旋转Y再旋转X
	对于情况二，发现就是对X旋转两次，先旋转到Y再旋转到X
	*/
	while (t[x].ff != goal)//一直旋转到X成为goal的儿子
	{
		int y = t[x].ff;//X的父亲 
		int z = t[y].ff;//X的爷爷
		if (z != goal)//如果Y不是根节点，则分为上面两类来旋转
		{
			if ((t[z].ch[0] == y) ^ (t[y].ch[0] == x))rotate(x);
			else rotate(y);
			/*
			注：t[y].ch[1]是y的右儿子，
			如果x是右儿子，
			那么这个式子是1，
			否则是0，
			也正好对应着左右儿子 
			*/ 
		} 
		rotate(x);
	}
	if (!goal)root = x;//如果goal是0，则将根节点更新为X 
} 

inline void find(int x)//查找X的位置并将其旋转到根节点
{
	/*
	//思路
	从根节点开始，左侧都比他小，右侧都比他大，
	所以只需要相应的往左/右递归
	如果当前位置的val已经是要查找的数
	那么直接把他Splay到根节点，方便接下来的操作
	类似于二分查找 
	*/ 
	int u = root;
	if(!u)return ;//树空
	while (t[u].ch[x > t[u].val] && x != t[u].val)//当存在儿子并且当前位置的值不等于x
	{
		u = t[u].ch[x > t[u]. val];//跳转到儿子，查找X的父节点	
	}	
	splay(u, 0);//把当前位置旋转到根 
} 

int main()
{
	
	return 0;	
}