二叉树（重刷）

一刷二叉树效果不好，没吃透，发现后面的动态规划和回溯都与之相关写不动，决定重刷，不好意思叫二刷

补充知识点

二叉树的分类（略）

二叉树主要有两种遍历方式

深度优先遍历：先往深走，遇到叶子节点再往回走。
广度优先遍历：一层一层的去遍历。

深度优先遍历

• 前序遍历（递归法，迭代法）
• 中序遍历（递归法，迭代法）
• 后序遍历（递归法，迭代法）

补充：一般情况下不适用中序遍历，左中右顺序不上不下太诡异了，深度从上到下前序，高度从下到上后续

广度优先遍历

• 层次遍历（迭代法）

注意返回值什么，是否需要保存，参考迭代

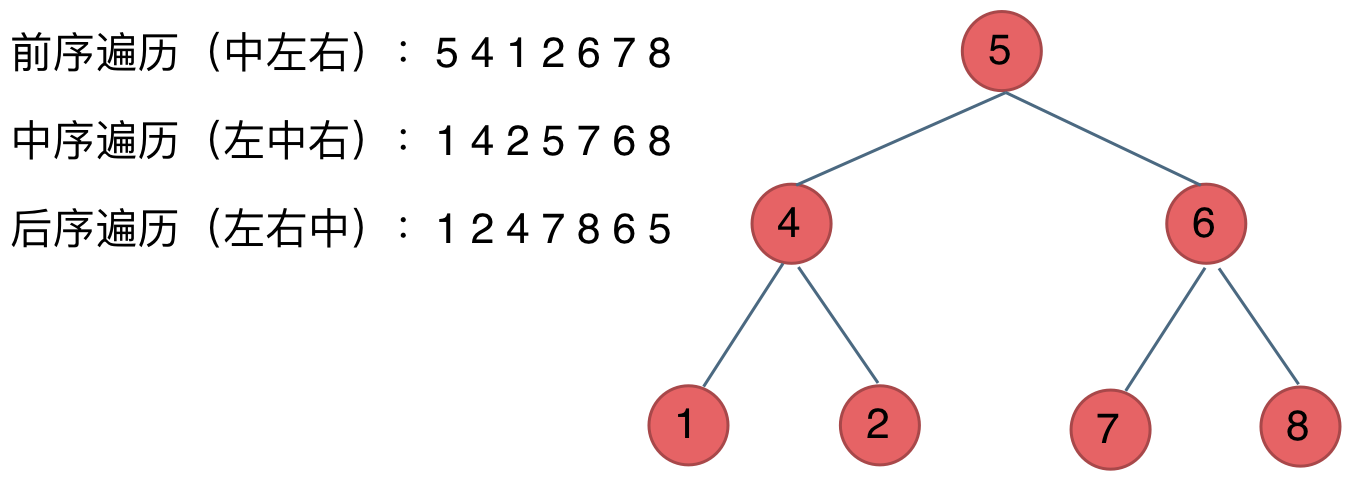
前中后，其实指的就是中间节点的遍历顺序

• 前序遍历：中左右
• 中序遍历：左中右
• 后序遍历：左右中

栈其实就是递归的一种实现结构，也就说前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来迭代实现的（不好用放弃）

广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

二叉树的定义

核心代码模式会忽略，但是这里要懂方便刷题

二叉树的存储结构可以使用数组和链表，数组不常用，使用链表

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

相对于链表 ，二叉树的节点里多了一个指针， 有两个指针，指向左右孩子，还有存储值的val

二叉树的存储方式

二叉树可以链式存储，也可以顺序存储。

那么链式存储方式就用指针， 顺序存储的方式就是用数组

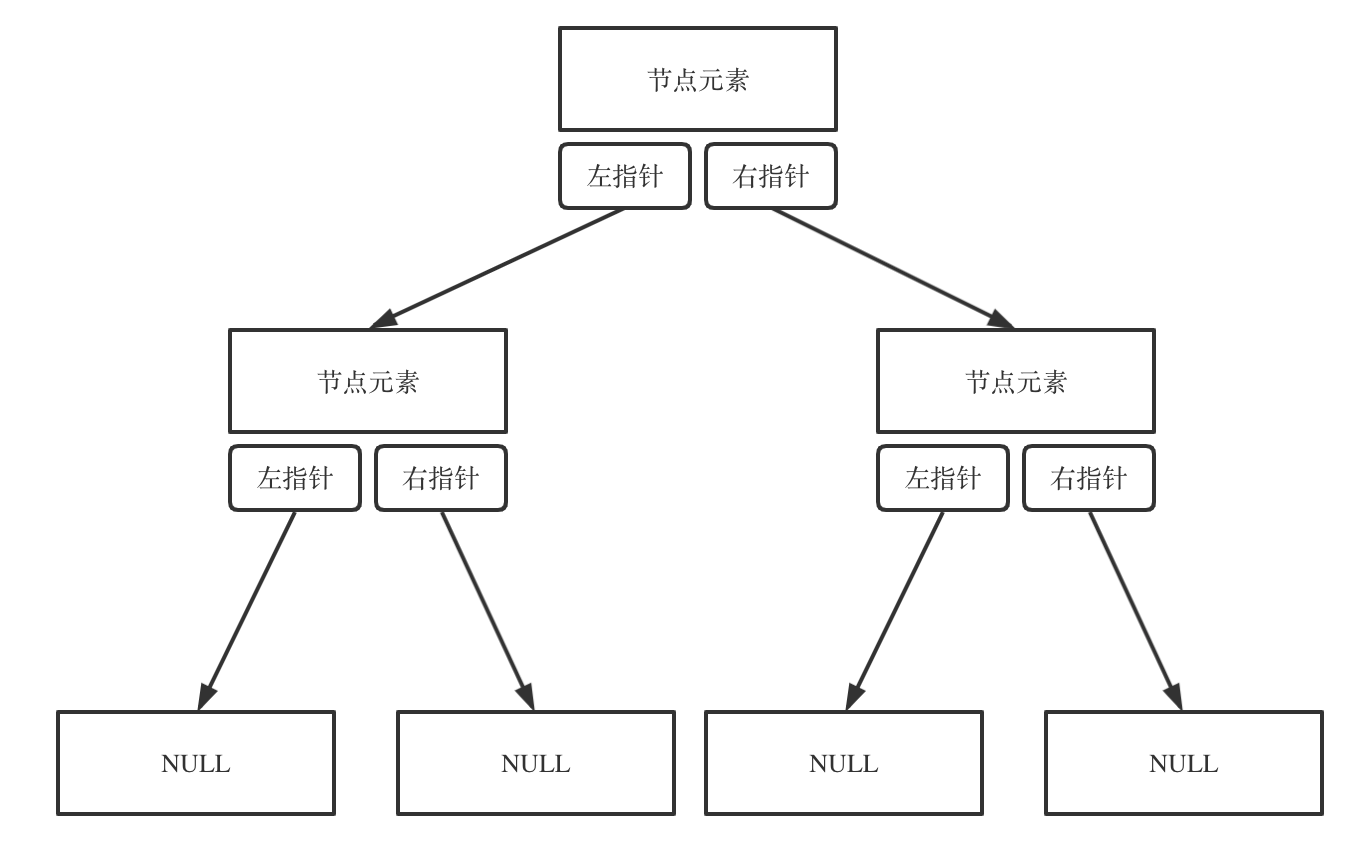
1.递归的前中后序遍历

递归三要素

前序遍历为例：

1.确定递归函数的参数和返回值：因为要打印出前序遍历节点的数值，所以参数里需要传入vector来放节点的数值，除了这一点就不需要再处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：

void traversal(TreeNode* cur, vector<int>& vec)

2.确定终止条件: 在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要结束了，所以如果当前遍历的这个节点是空，就直接return，代码如下：

if (cur == NULL) return;

3.确定单层递归的逻辑：前序遍历是中左右的循序，所以在单层递归的逻辑，是要先取中节点的数值，代码如下：

vec.push_back(cur->val);    // 中
traversal(cur->left, vec);  // 左
traversal(cur->right, vec); // 右

前序遍历：

class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

一个自动生产二叉树结构的函数，里面有左右指针和保存元素的val
定义一个result数组保存遍历的元素，最后返回结果
递归开始传入参数

明确返回值和传入需要的参数
传入的节点判空，用于直接返回或者跳出节点递归null结束的标志
开始中左右的前序遍历，每次递归节点指向以及用数组保存值，左节点不断递归NULL交给右节点直到无递归逻辑，结束返回值

中其实就是专门来保存左右节点传过来的值的

中后类似

二叉树的迭代遍历

栈其实就是递归的一种实现结构，也就说前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来迭代实现的（不好用放弃）

前序遍历（迭代法）

前序遍历是中左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子。

为什么要先加入 右孩子，再加入左孩子呢？ 因为这样出栈的时候才是中左右的顺序。

锐评：上比不过递归前中后通用，下比不过层序快捷

二叉树层序遍历登场

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 就是从左到右一层一层的去遍历二叉树

已知传统三类遍历无法横向遍历，

需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

二叉树层序遍历的模板（神中神）

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

用一个队列来保存节点，在确定判空后push头节点，用一个二维数组来保存最终结果
在队列不为空的情况循环，确定队列长度以此保证在循环的过程中固定取出当前层数的节点
使用一个一维数组保存一层的结果

循环，队列弹出头结点，保存，放入该节点的数值进入一维数组，然后从左到右不为空就放入节点进入队列（模拟队列层序），依次循环的时候左节点右节点由于队列的特性不会混乱，

执行完一层后会跳出来重新计算队列大小，在有左右节点的情况下，每次放每个节点对应的左右节点，但是会在下一次使用，因为根据队列特性还需要弹出上层的右节点对应数值

知道最后取不出节点就判空，将以为数组放入二维数组返回整体二维数组

层序遍历类似题汇总

二叉树的层次遍历 II

给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

层序遍历是自上向下

二叉树的层序遍历，就是最后把result数组反转一下就可以了

reverse(result.begin(), result.end()); // 在这里反转一下数组即

二叉树的右视图

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。(整体的右节点)

层序遍历的时候，判断是否遍历到单层的最后面的元素，如果是，就放进result数组中，随后返回result就可以了。

if (i == (size - 1)) result.push_back(node->val); // 将每一层的最后元素放入result数组中 每一层的最后一个元素肯定是最右边的，记不住的话就记住这个公式，这里不需要二维数组，存放的都是一维的值

二叉树的层平均值

给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。

本题就是层序遍历的时候把一层求个总和在取一个均值。

            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                sum += node->val;
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(sum / size); // 将每一层均值放进结果集
        }
        return result;

N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

可能有多个子节点，不能单使用左右节点了

 for (int i = 0; i < size; i++) {
                Node* node = que.front();
                que.pop();
                vec.push_back(node->val);
                for (int i = 0; i < node->children.size(); i++) { // 将节点孩子加入队列
                    if (node->children[i]) que.push(node->children[i]);
                }
            }

遍历题目以及给出的子节点这一层的节点个数来代替

在每个树行中找最大值

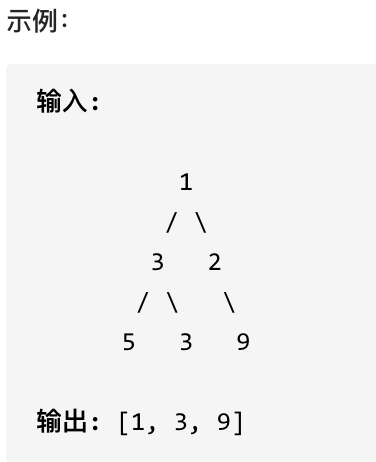
层序遍历，取每一层的最大值

maxValue = node->val > maxValue ? node->val : maxValue;
result.push_back(maxValue); // 每层遍历完把最大值放进数组

填充每个节点的下一个右侧节点指针

脱离模板放弃

二叉树的最大深度

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

返回它的最大深度 3 。

一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == NULL) return 0;
        int depth = 0;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++; // 记录深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return depth;
    }
};

只需要返回大小就行，结果集,每层遍历前记录一次

二叉树的最小深度

需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点

class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == NULL) return 0;
        int depth = 0;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++; // 记录最小深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
                if (!node->left && !node->right) { // 当左右孩子都为空的时候，说明是最低点的一层了，退出
                    return depth;
                }
            }
        }
        return depth;
    }
};

翻转二叉树

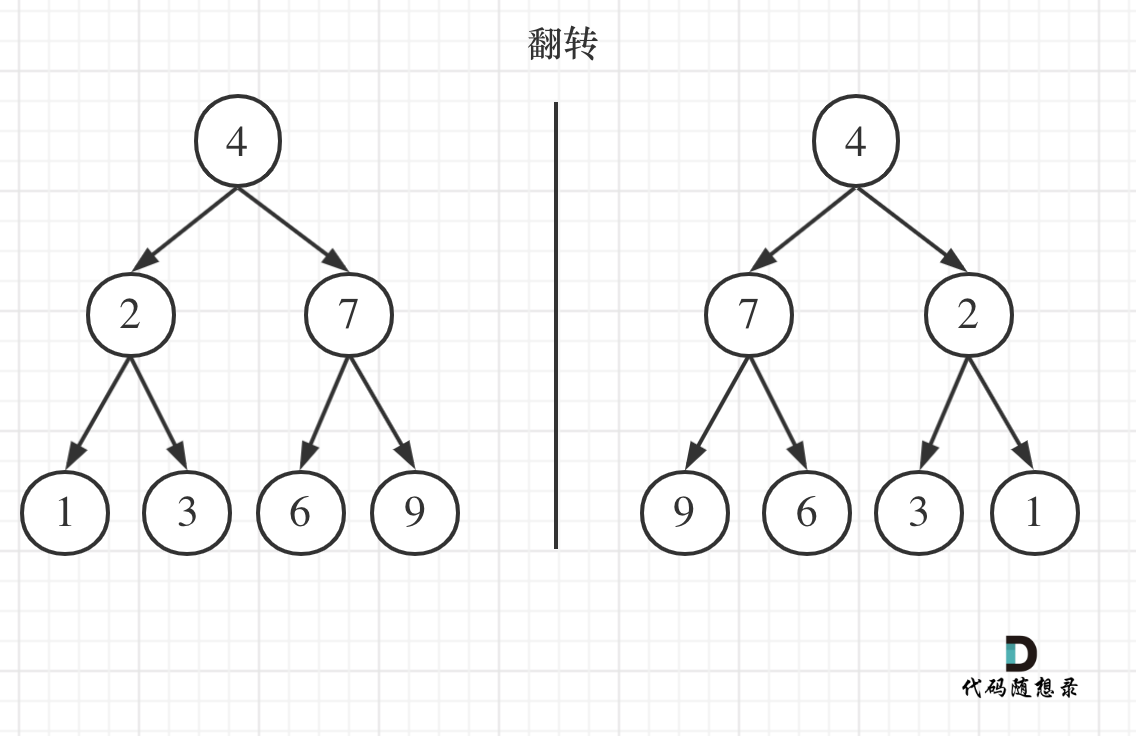
递归法

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL) return root;
        swap(root->left, root->right);  // 中
        invertTree(root->left);         // 左
        invertTree(root->right);        // 右
        return root;
    }
};

这里不需要存放值，只需要返回头结点就行了，常见三件套看之前
先交换左右节点再交换左右树整体

广度优先遍历

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                swap(node->left, node->right); // 节点处理
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return root;
    }
};

简单，交换，返回头结点就可以了

完全二叉树的节点个数

class Solution {
public:
    int countNodes(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        int result = 0;
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                result++;   // 记录节点数量
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return result;
    }
};

每次遍历记录节点个数就行了

对称二叉树

只能使用递归
这里不班门弄斧了看题解
首先想清楚，判断对称二叉树要比较的是哪两个节点，要比较的可不是左右节点！

平衡二叉树

只能使用递归
班门弄斧不记录了