Matlab数组和向量

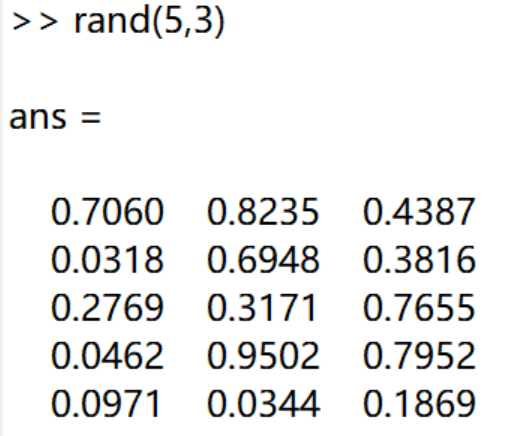
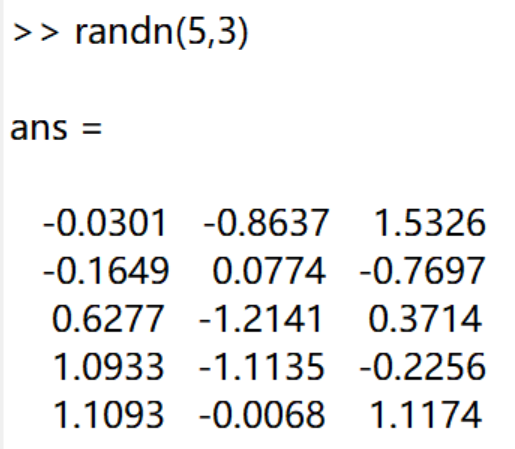
rand（m,n）与randn（m,n）的作用都是产生m行n列的随机数组，其区别如下：

rand（）是平均分布，即等概率分布，等概率产生0-1范围内的数。

randn（）是标准正态分布，均值为0，标准差为1。

 size()函数：

当其应用于n维数组A时，函数size(A)作用如下:

1.如果按照只有一个返回值的情况调用，将会返回一个n维向量，其中包含数组的每一维的大小。

2.如果按照具有多个返回值的情况调用，将返回具有所要求数量的数组A 的各维大小。所以，应当给定与数组维数相同的变量个数。

 length（）函数：

length函数将返回数组的最大维值。

zeros（）与ones（）函数：

其将分别产生填充值为0或1的m行n列数组

 

 

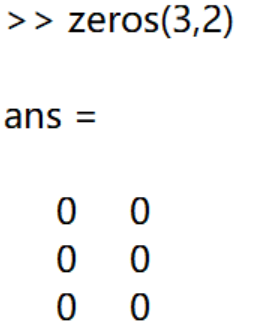
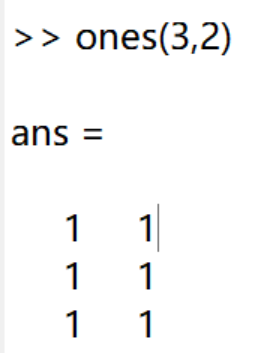
 diag（）函数：

diag（）函数有多种形式，其中最常用的为以下两种：

1.A为一数组，diag（A）将A中对角线上的元素作为向量返回

2.V为一向量，diag（V）将返回一条对角线为V的方阵。

 

另外：diag（diag（A））将返回一个对角线为A中对角线上的元素的方阵。

 

 

 

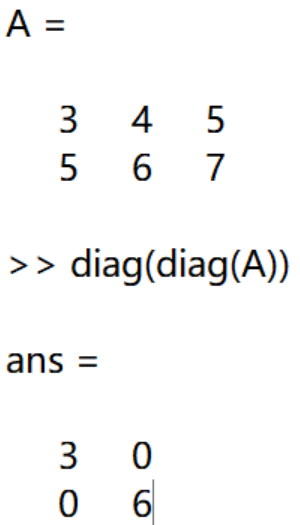
 magic（）函数：

magic（m）函数产生一个填充1到m^2之间数字的数组，其组织方式使得每一行，每一列以及对角线上的元素分别加起来等于相同的数。

 

 

 

 

 

 .*”和“*”的区别:

1.在进行数之间的运算时“.*”和“*”是没有区别的，都是表示普通的乘法运算。

 

 

 2.在进行矩阵之间的运算时“.*”和“*”的意义就有所不同了。假设a，b表示两个矩阵，a*b表示矩阵a与矩阵b进行矩阵相乘，a.*b表示矩阵a中的元素与矩阵b中的元素按位置依次相乘，得到的结果将作为新矩阵中相同位置的元素。

 

 

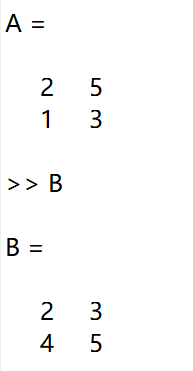
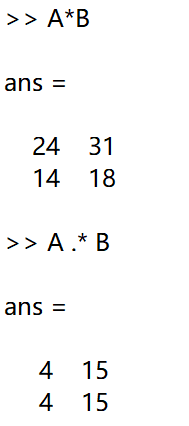
 下面给出的是matlab一些常见的数组和矩阵运算。

1. 数组加法：A+B，数组加法和矩阵加法相同。

2. 数组减法：A-­B ，数组减法和矩阵减法相同。

3. 数组乘法：A.*B，A 和 B 的元素逐个对应相乘，两数组之间必须有相同的形，或其中一个是标量。

4. 矩阵乘法：A*B，A 和 B 的矩阵乘法，A 的列数必须和 B 的行数相同。

5. 数组右除法：A./B，A 和 B 的元素逐个对应相除：A(i,j)/B(i,j)两数组之间必须有相同的形，或其中一个是标量。

6. 数组左除法：A.\B，A 和 B 的元素逐个对应相除：B(i,j)/A(i,j)两数组之间必须有相同的形，或其中一个是标量。

7. 矩阵右除法：A/B 矩阵除法，等价于 A*inv(B)， inv(B)是 B 的逆阵。

8. 矩阵左除法：A\B 矩阵除法，等价于 inv(B)*A， inv(A)是 A 的逆阵。

9. 数组指数运算：A.^B，AB中的元素逐个进行如下运算：A(i,j)^B(i,j)，A(i,j)/B(i,j)两数组之间必须有相同的形，或其中一个是标量。

 sum()函数：

　　　对于一维数组（行向量）或者列向量，使用 sum( A ) 即可对该数组求和。

　　　　对于二维数组，使用sum（A)会返回一个向量，为A中每一列的和。

　　　　如果要计算整个二维数组的和，可以使用sum（sum(A))

 

　　　　

 

 

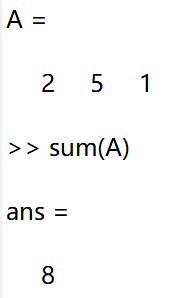
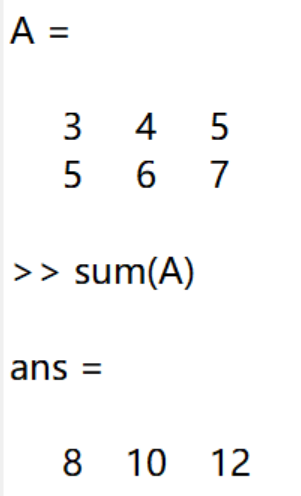
 mean()函数：

　　　　对于一维数组（行向量）或者列向量，使用 mean( A ) 即可对该数组求平均数。

　　　　对于二维数组，使用mean（A)会返回一个向量，为A中每一列的平均数。

　　　　如果要计算整个二维数组的平均数，可以使用mean（mean(A))

　　　　

 

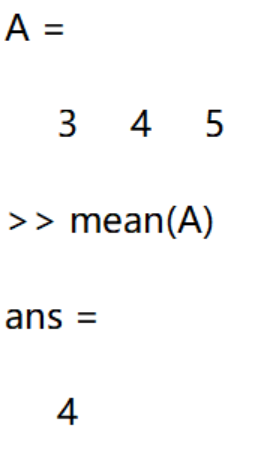
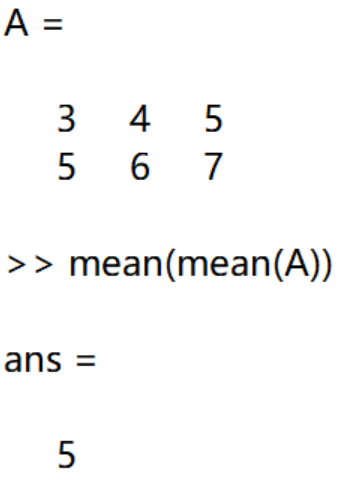
 min()与max（）函数：

　　　　min（）与max（）返回两个行向量：每一列的最大值或者最小值以及它们在每一列中出现的行号。

　　　　

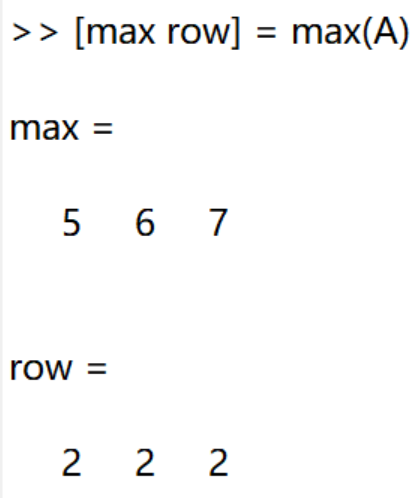
 数组重排：

　　　　reshape（）函数：

　　　　　　　　reshape（）函数不会填充空白位置，且原始数组维数的乘积必须与新数组维数乘积相等。