【刷题笔记】p9197 摩天大楼

【刷题笔记】p9197 摩天大楼

题意

将互不相同的 \(N\) 个整数 \(A_1,A_2,⋯,A_N\) 按照一定顺序排列。假设排列为 \(f_1,f_2,⋯,f_N\)，要求：\(|f1−f2|+∣f2−f3∣+⋯+∣f_{N-1}−f_N∣\le L\)。
满足题意的排列的方案数对 \(10^9+7\) 取模后的结果。

思路

首先注意到题目对排列的 具体顺序 没有很强的限制，但是却对 值的大小 有很强的限制。所以考虑将 \(a\) 序列排序后，从大到小扫。

看下面的一张图

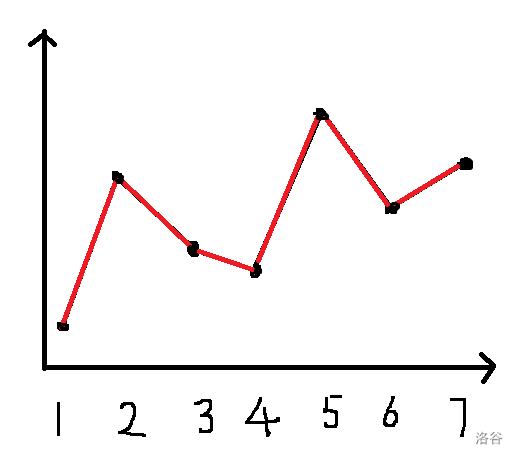
绝对值的和就是所有红线两端点 纵坐标差的和，所以考虑将 \(a\) 序列从大到小排序后，扫描线。

每次从大到小加入 \(a_i\)，那么新增加的贡献就是，\(（a_{i-1}-a_i)\times 2\times 连续段的个数\)（下图绿色部分）：

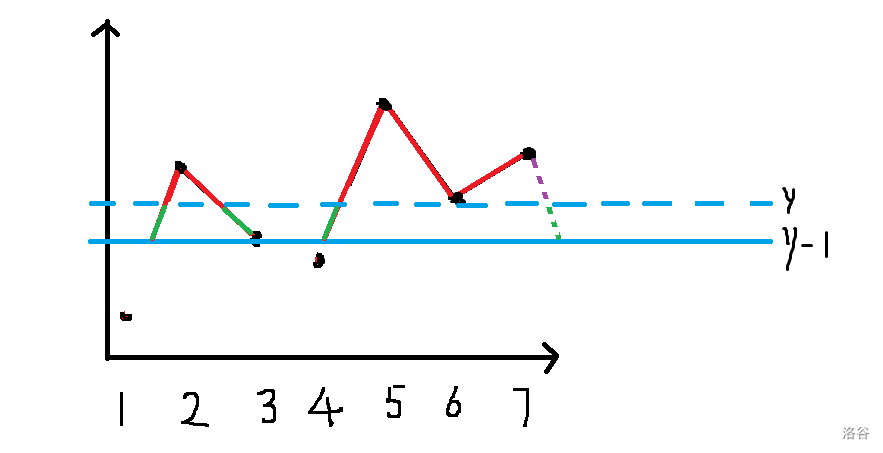
不过注意到当最后一个数已经插入时，后面不能再算贡献（绿色紫色虚线部分），同理，第一个数已经插入时前面不能再算贡献。于是设 \(dp_{i,j,0/1,0/1}\) 表示目前已经有 \(i\) 个连续段，和为 \(j\)，第一个数/最后一个数有没有被加进去，答案就是 \(dp_{1,≤L,1,1}\)。

转移的话大致有三种：

• 这个数新开了一个段，段数 \(+1\)。
• 这个数合并了两段，段数 \(−1\)。
• 这个数延续了其中一段，段数不变。

时间复杂度 \(O(n^2L)\)，足以通过。