20211316郭佳昊 《信息安全系统设计与实现(上)》 第八周学习总结
一、任务要求
[ 1 ] 知识点归纳以及自己最有收获的内容,选择至少2个知识点利用chatgpt等工具进行苏格拉底挑战,并提交过程截图,提示过程参考下面内容 (4分)
我在学***X知识点,请你以苏格拉底的方式对我进行提问,一次一个问题
核心是要求GPT:请你以苏格拉底的方式对我进行提问
然后GPT就会给你提问,如果不知道问题的答案,可以反问AI:你的理解(回答)是什么?
如果你觉得差不多了,可以先问问GPT:针对我XXX知识点,我理解了吗?
GPT会给出它的判断,如果你也觉得自己想清楚了,可以最后问GPT:我的回答结束了,请对我的回答进行评价总结,让它帮你总结一下。
[ 2 ] 问题与解决思路,遇到问题最先使用chatgpt等AI工具解决,并提供过程截图(3分)
[ 3 ] 实践过程截图,代码链接(2分)
[ 4 ] 其他(知识的结构化,知识的完整性等,提交markdown文档,使用openeuler系统等)(1分)
二、知识点总结
并行计算
并行计算是一种计算方案,它尝试使用多个执行并行算法的处理器更快速地解决问题。
顺序算法与并行算法
- 顺序算法:用一个begin-end代码块列出,可能包含多个步骤,每个步骤通过单个任务依次执行,所有步骤完成时,算法结束。
- 并行算法:使用cobegin-coend代码块列出,所有任务并行执行。
![]()
并行性与并发性
在单CPU系统中,并发性是通过多任务处理来实现的。
线程
线程的原理
线程是某进程同一地址空间上的独立执行单元
线程的优点
- 线程创建和切换速度更快
- 线程的响应速度更快
- 线程更适合并行计算
线程的缺点
- 由于地址空间共享,线程需要来自用户的明确同步
- 许多库函数可能对线程不安全
- 单CPU系统上,使用线程解决问题实际上比使用顺序程序慢,原因在于运行时创建线程和切换上下文的系统开销
线程操作
线程的执行轨迹与进程类似,线程可以在内核模式或用户模式下执行,在用户模式下,线程在进程的相同地址空间中执行
线程管理函数
创建线程
使用pthread_create()函数创建线程。成功返回0,失败则返回错误代码。
int pthread_create(pthread_t *pthread_id,pthread_attr_t *attr,void *(*func)(void*),void *arg)
参数如下:
- pthread_id是指向pthread_t类型变量的指针,会被操作系统内核分配的唯一线程ID填充
- attr是指向另一种不透明数据类型的指针
- func是要执行的新线程函数的入口地址
- arg是指向线程函数参数的指针,可写为
void *func(void *arg)
线程ID
线程ID是一种不透明的数据类型,取决于实现情况,不直接比较线程ID,可以用pthread_equal()函数进行比较int pthread_equal (pthread_t t1, pthread_t t2)线程不同返回0,否则返回非0。
线程终止
线程函数结束后,线程即终止,或调用int pthread_exit (void *status)进行显式终止,返回0正常终止,否则异常终止。
线程链接
一个线程可以等待另一个线程的终止,通过int pthread_join (pthread_t thread, void **status_ptr)终止线程的退出状态以status_ptr返回。
线程示例程序
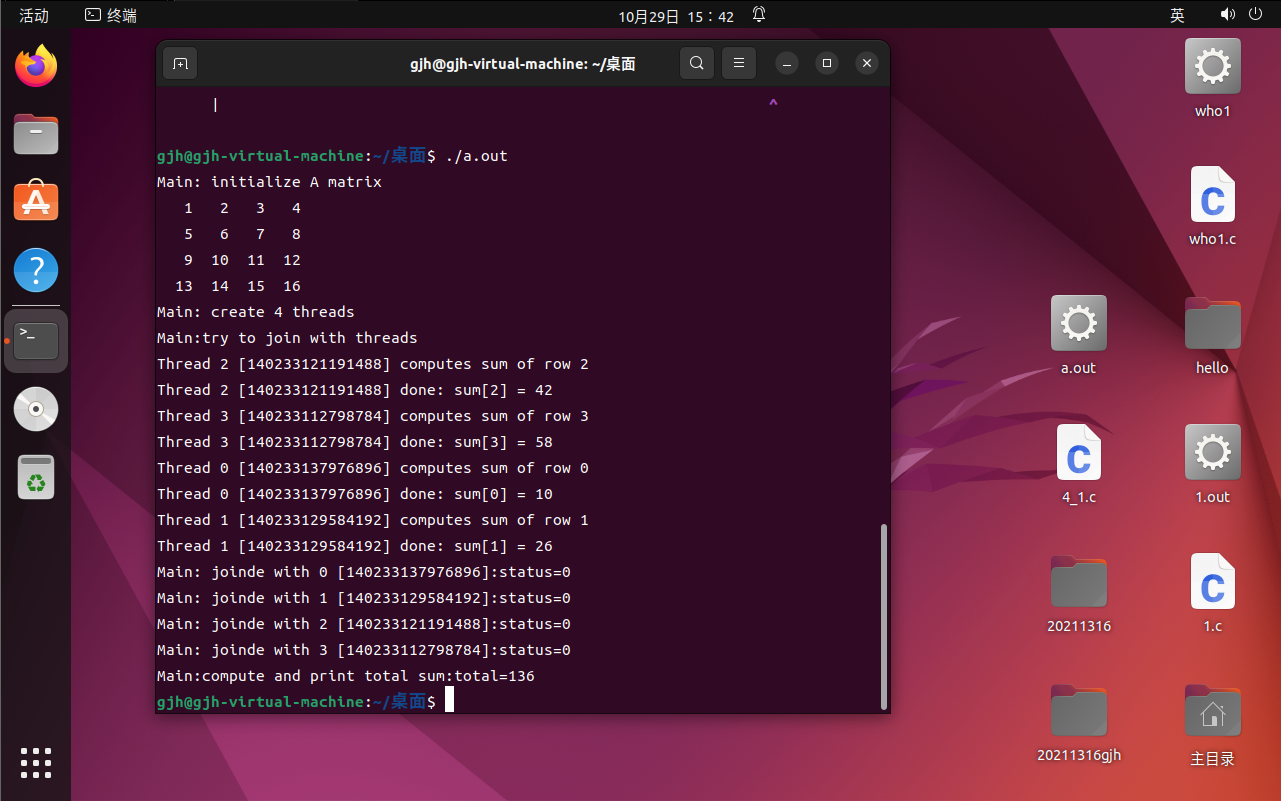
用线程计算矩阵的和
#include <stdio.h>
#include <stdlib.h>
#include <pthread.h>
#define N 4
int A[N][N], sum[N];
void *func(void *arg)
{
int j, row;
pthread_t tid = pthread_self(); // get thread ID number
row = (int)arg; // get row number from arg
printf("Thread %d [%lu] computes sum of row %d\n", row, tid, row);
for (j=0; j<N; j++)
{
sum[row] += A[row][j];
}
printf("Thread %d [%lu] done sum[%d] = %d\n",row, tid, row, sum[row]);
pthread_exit((void*)0); // thread exit: 0=normal termination
}
int main (int argc, char *argv[])
{
pthread_t thread[N]; // thread IDs
int i, j, r, total = 0;
void *status;
printf("Main: initialize A matrix\n");
for (i=0; i<N; i++)
{
sum[i] = 0;
for (j=0; j<N; j++)
{
A[i][j] = i*N + j + 1;
printf("%4d" ,A[i][j]);
}
printf("\n");
}
printf("Main: create %d threads\n", N);
for(i=0; i<N; i++)
{
pthread_create(&thread[i], NULL, func, (void *)i);
}
printf("Main: try to join with threads\n");
for(i=0; i<N; i++)
{
pthread_join(thread[i], &status);
printf("Main: joined with %d [%lu]: status=%d\n",i, thread[i], (int)status);
}
printf("Main: compute and print total sum:");
for (i=0; i<N; i++)
{
total += sum[i];
}
printf("tatal = %d\n", total);
pthread_exit(NULL);
}
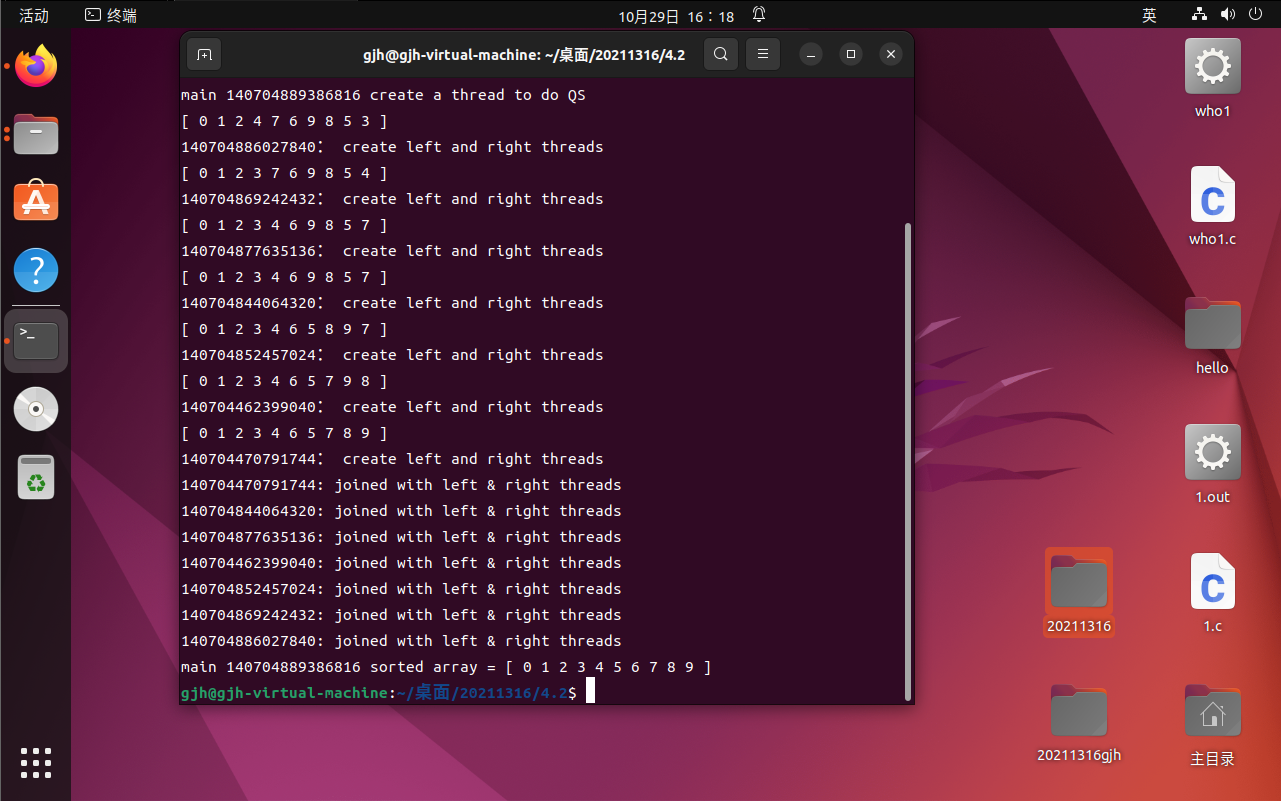
用线程快速排序
#include <stdio.h>
#include <stdlib.h>
#include <pthread.h>
#include <math.h>
#define N 4
double A[N][N+1];
pthread_barrier_t barrier;
int print_matrix()
{
int i, j;
printf("----------------------------\n");
for(i=0; i<N; i++)
{
for(j=0; j < N+1; j++)
printf("%6.2f ", A[i][j]);
printf("\n");
}
}
void *ge(void *arg) // threads function: Gauss elimination
{
int i, j, prow;
int myid = (int)arg;
double temp, factor;
for(i=0; i<N-1; i++)
{
if (i == myid)
{
printf("partial pivoting by thread %d on row %d: ", myid, i);
temp = 0.0; prow = i;
for (j=i; j<=N; j++)
{
if (fabs(A[j][i]) > temp)
{
temp = fabs(A[j][i]);
prow = j;
}
}
printf("pivot_row=%d pivot=%6.2f\n", prow, A[prow][i]);
if (prow != i) // swap rows
{
for (j=i; j<N+1; j++)
{
temp = A[i][j];
A[i][j] = A[prow][j];
A[prow][j] = temp;
}
}
}
// wait for partial pivoting done
pthread_barrier_wait(&barrier);
for(j=i+1; j<N; j++)
{
if (j == myid)
{
printf("thread %d do row %d\n", myid, j);
factor = A[j][i]/A[i][i];
for (int k=i+1; k<=N; k++)
A[j][k] -= A[i][k]*factor;
A[j][i] = 0.0;
}
}
// wait for current row reductions to finish
pthread_barrier_wait(&barrier);
if (i == myid)
print_matrix();
}
}
int main(int argc, char *argv[])
{
int i, j;
double sum;
pthread_t threads[N];
printf("main: initialize matrix A[N][N+l] as [A|B]\n");
for (i=0; i<N; i++)
for (j=0; j<N; j++)
A[i][j] = 1.0;
for (i=0; i<N; i++)
A[i][N-i-1] = 1.0*N;
for (i=0; i<N; i++)
{
A[i][N] = 2.0*N - 1;
}
print_matrix(); // show initial matrix [A|B]
pthread_barrier_init(&barrier, NULL, N); // set up barrier
printf("main: create N=%d working threads\n", N);
for (i=0; i<N; i++)
{
pthread_create(&threads[i], NULL, ge, (void *)i);
}
printf("main: wait for all %d working threads to join\n", N);
for (i=0; i<N; i++)
{
pthread_join(threads[i], NULL);
}
printf("main: back substitution :");
for (i=N-1; i>=0; i--)
{
sum = 0.0;
for (j=i+1; j<N; j++)
sum += A[i][N];
A[i][N] = (A[i][N]- sum)/A[i][i];
}
// print solution
printf("The solution is :\n");
for(i=0; i<N; i++)
{
printf("%6.2f ",A[i][N]);
}
printf("\n");
}
线程同步
由于线程在进程的同一地址空间中执行,它们共享同一地址空间中的所有全局变量和数据结构,当多个线程试图修改同一共享变量或数据结构时,如果修改结果取决于线程的执行和、顺序,则称之为竞态条件。
互斥量
在Pthread中,锁被称为互斥量,意思是相互排斥,互斥变量用pthread_mutex_t类型声明的,使用前需要初始化
死锁预防
死锁是一个状态,在这种状态下,许多执行实体相互等待,无法继续进行下去
信号量
信号量说是进程同步的一般机制,计数信号量是一种数据结构
struct sem{
int value;
struct process *queue
}s
三、苏格拉底挑战









 浙公网安备 33010602011771号
浙公网安备 33010602011771号