2025多校冲刺省选模拟赛3

神秘 IOI 赛制。

T1、等差

因为是 IOI 赛制，所以赛时过了整整一车的假做法，包括但不限于什么写了两份假做法，一份发现后面的点 T 了，另一份发现前面的都 WA 了，但后面的过了，而且他们两个的并集等于全集，于是发挥了一下传统手艺，将两份代码拼在一起，然后就过题啦！

先讲一下我的假做法吧，就是你发现对于同样的长度 $ n $ ，如果 $ k $ 可以构成等差数列的话，那么 $ x k , x ∈ N_+ $ 都可以，于是可以用他来优化一下，求出对于每个 $ k $ 最长可以使他合法的长度是多少，成为 $ r_k $ ，然后判断答案时看看符合题目范围的 $ k $ 里 $ r_k $ 最大值是否 $ \ge i $ 即可。

上面的做法并不能真正的优化复杂度，只是让他大概率跑不满而已，所以我们需要更快的判断对于一个长度 $ n $ ， $ k $ 是否合法。

这个东西应该只有哈希能做了。

我们正常去判这个东西的时候，应该是逐个抽出来 $ a_{i+1} , a_{2i+1} , a_{3i+1} ...... , i \lt k $ 每一个数列，然后去判他是不是等差数列，我们考虑转化一下，这相当于判对于每一个位置 $ i , i+2k \le n $ ，满足 $ a_{i} - a_{i+k} = a_{i+k} - a_{i+2k} $ 。

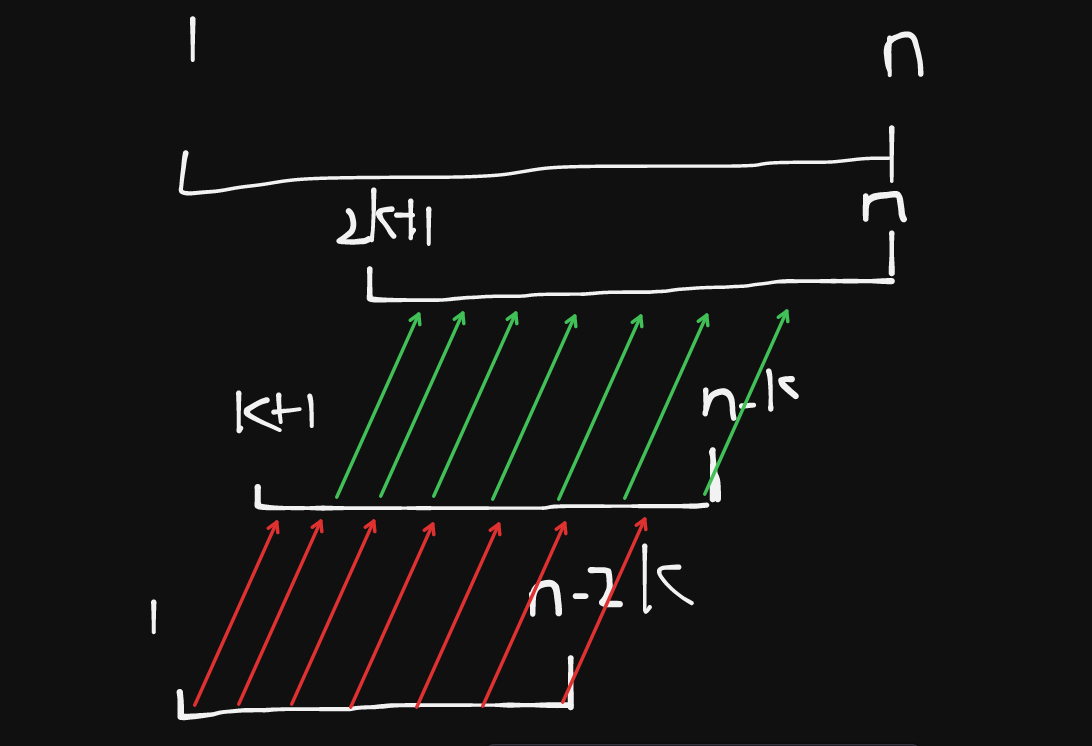
如图，每条边表示两端相减的值，那么我们相当于要判断每一条红遍和对应的绿边依次相等，我们把它看成字符串，然后直接哈希判等即可。

码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mk make_pair
#define ps push_back
const int N=2e6+10,inf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f,mod=1e9+7;
inline ll read(){
	char c=getchar();ll x=0;bool f=0;
	while(!isdigit(c))f=c=='-'?1:0,c=getchar();
	while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return f?-x:x;
}
const ull B=1145141113;
int n,a[N],mx[N];
ll num;
ull hx[N],ci[N];
inline ull hs(int l,int r){return hx[r]-hx[l-1]*ci[r-l+1];}
inline void sol(){
	for(int i=1;i<=n;++i){
		mx[i]=2*i;
		int l=mx[i]+1,r=n,mid;
		while(l<=r){
			mid=l+r>>1;
			if(hs(1,mid-i*2)-hs(i+1,mid-i)==hs(i+1,mid-i)-hs(2*i+1,mid))mx[i]=mid,l=mid+1;
			else r=mid-1;
		}
	}
}
signed main(){

	// #ifndef ONLINE_JUDGE
	freopen("arithmetic.in","r",stdin);
	freopen("arithmetic.out","w",stdout);
	// #endif

	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	n=read();
	ci[0]=1;
	for(int i=1;i<=n;++i){
		a[i]=read();
		ci[i]=ci[i-1]*B,hx[i]=hx[i-1]*B+a[i];
	}
	sol();
	int man=0;
	for(int i=1,j=1;i<=n;++i){
		while(j<=((i-1)>>1))man=max(man,mx[j++]);
		if(man>=i)putchar('1');
		else putchar('0');
	}
}

T2、叉积

赛时先推了半个小时叉积是啥，然后会了 $ n^2 $ 做法，写了个凸包，然后忘了特判 $ \Delta x = 0 $ 的情况，WA了 12 pts。

先说 $ n^2 $ 的，我们考虑最后答案是 $ ans = \sum_{i=l}^{r} b_{i} x - \sum_{i=l}^{r} a_i y $ ，然后整体除以 $ x $ 并移项，得到 $ \frac{ans}{x} + \frac{y}{x} \sum_{i=l}^{r} a_i = \sum_{i=l}^{r} b_i $ ，类似于斜率优化的形式，我们类比进行考虑，将 $ \frac{ans}{x} $ 当做截距， $ \frac{y}{x} $ 是斜率，有点集 $ (\sum_{i=l}^{r} a_i , \sum_{i=l}^{r} b_i) , 1 \le l \le n , l \le r \le n $ ，我们直接把 $ n^2 $ 个点枚举出来将他们见一个凸包，然后直接询问即可（想要好写一点的话，可以分别维护一个上凸壳和一个下凸壳）。

然后考虑怎么优化这个东西，维护凸包应该是不可避免的吧，但我们又不能直接枚举所有的点。然后需要用到一些神秘算法。

接下来介绍一下 闵可夫斯基和 ：

先推一篇博客：wqs二分&闵可夫斯基和学习笔记

首先这个东西是用来求两个向量集合相加的向量集合，即 $ x ∈ A , y ∈ B , x + y ∈ C $ ，的 C 集合，截一张网上的图：

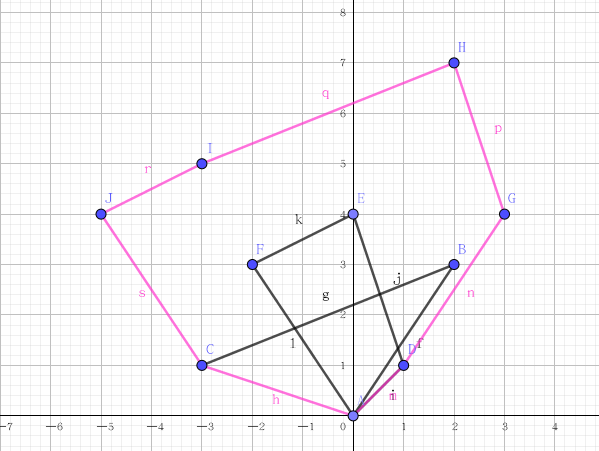
两个黑色的区域分别是 $ A,B $ 粉色的是 $ C $ ，可以看做是两个图形，一个图形 $ A $ 绕着 $ B $ 的边界走了一圈，走过的点的集合 $ C $ ，很形象对吧。

那么怎么求呢？

首先凸包就是由两个凸壳组成的，那么我们只讲凸壳（因为凸包没写过，不敢胡）怎么做。

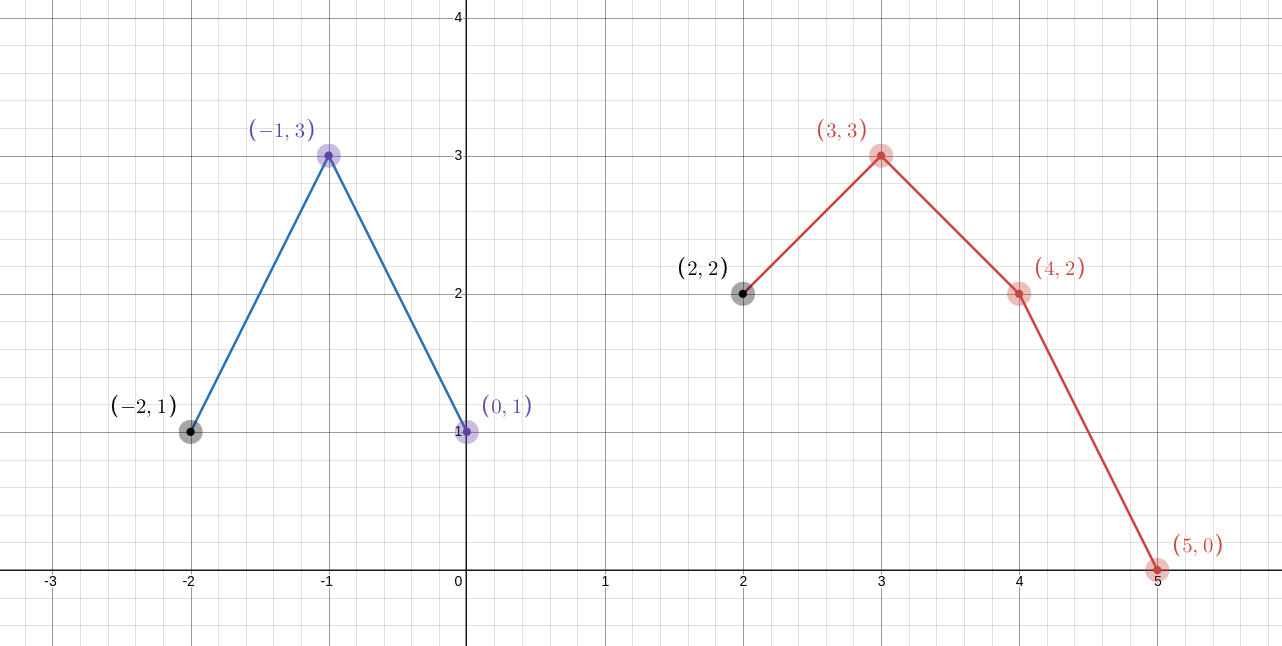
对于上凸壳，我们直接拿出两凸壳最左侧的两个点 $ x , y $ ，那么最终的凸壳里一定有 $ x + y $ 这个点，所以我们先把这个点加进去。

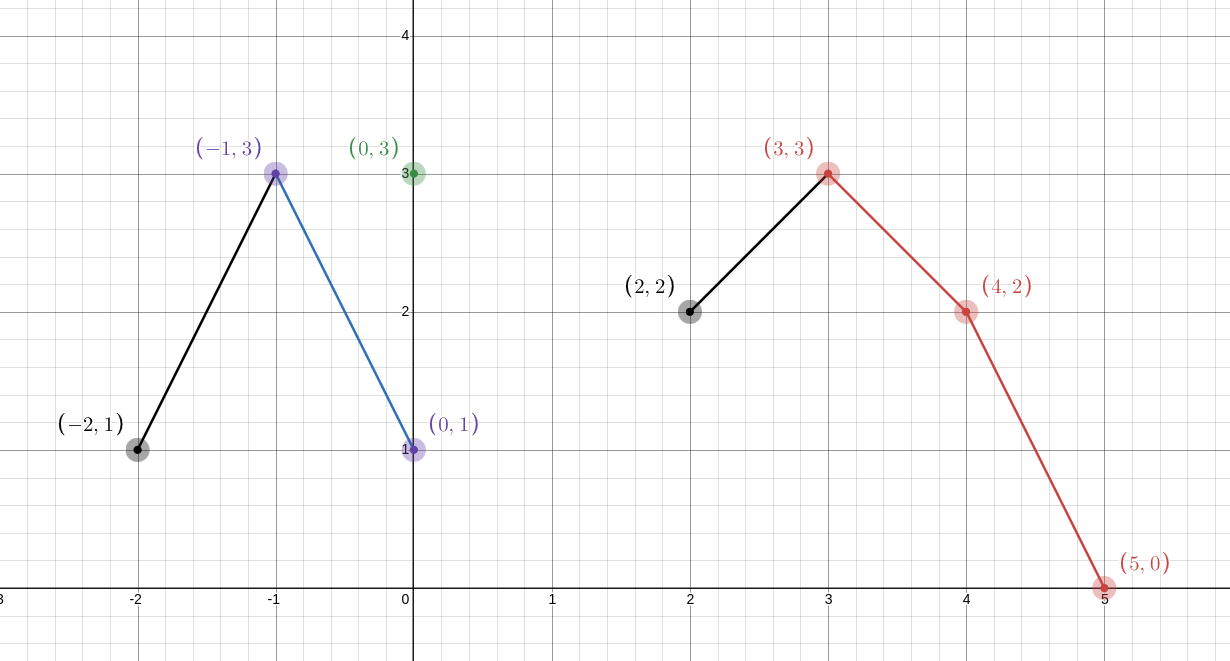
然后我们去比较他们俩连着的那条边的斜率，谁斜率大，就把谁及连着的那个点加进去

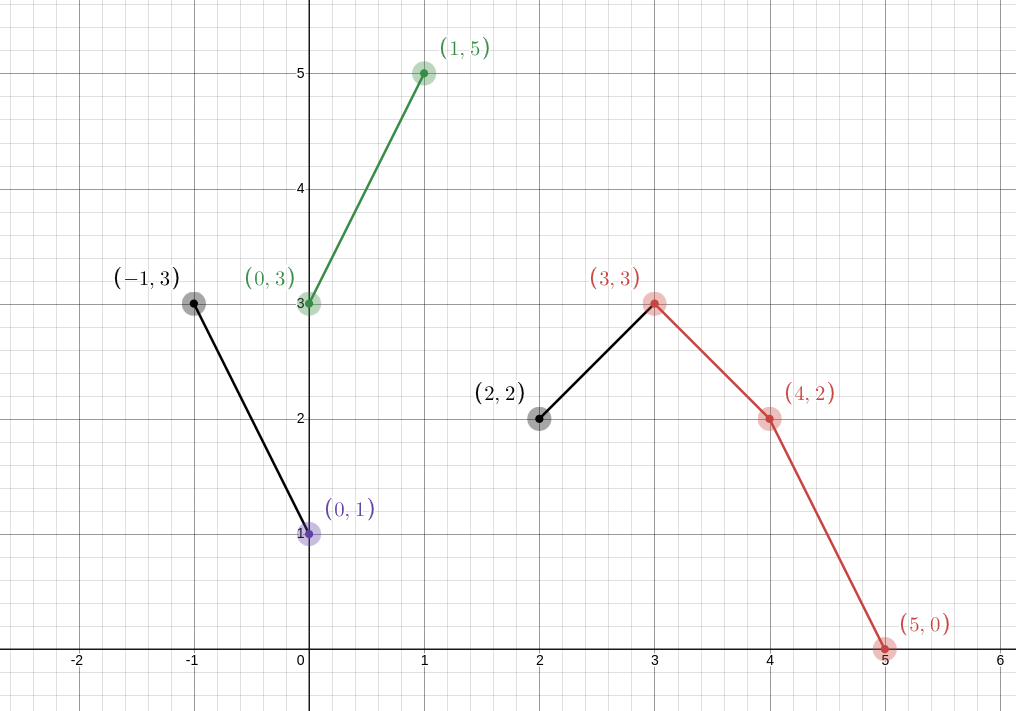
然后一直这样比较直到将所有的点的加进去

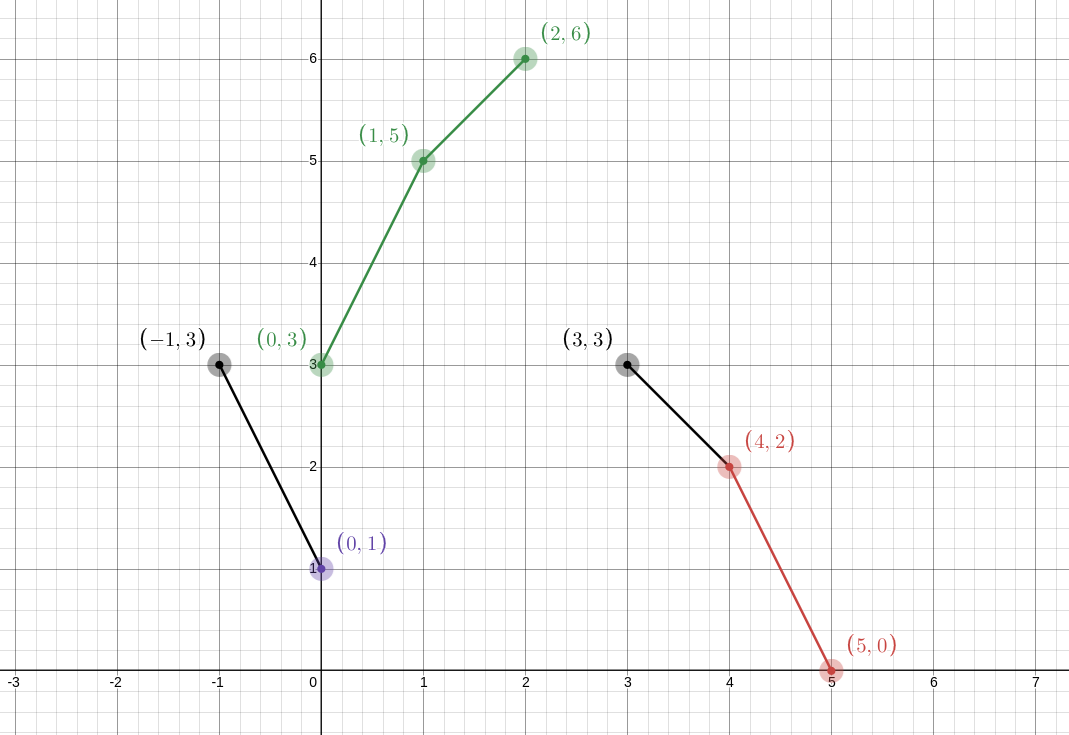
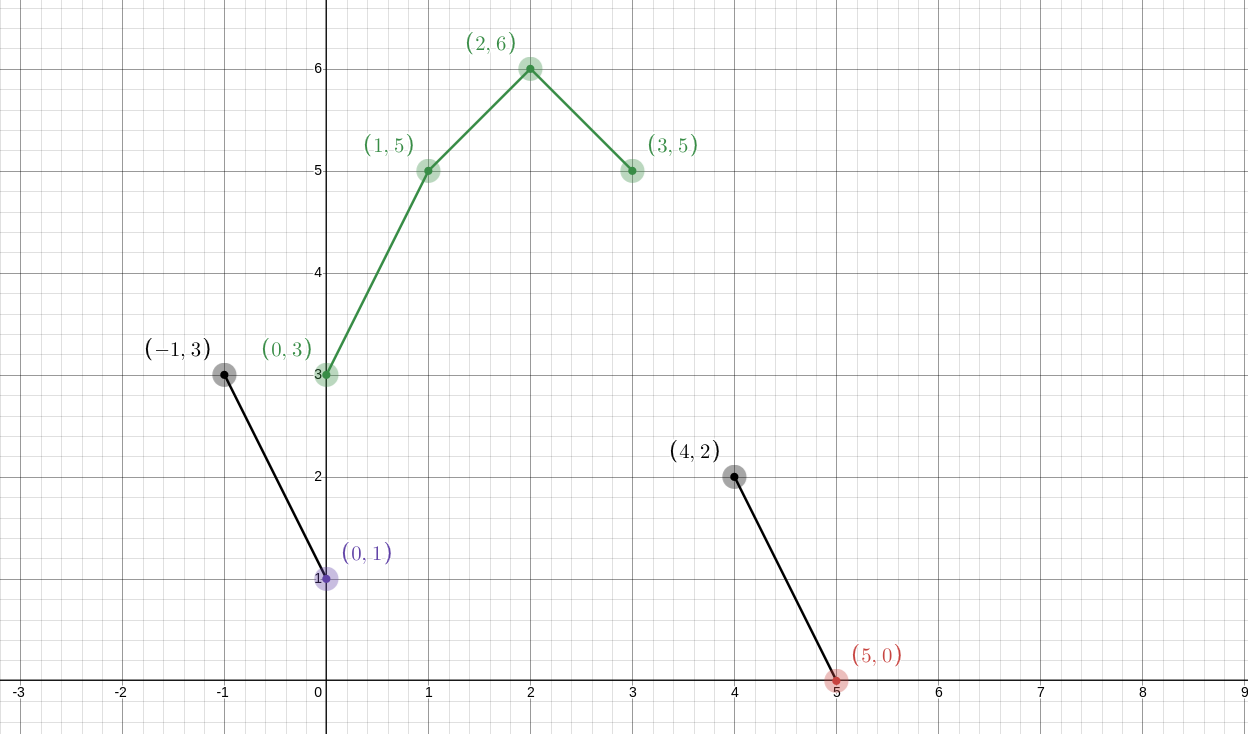
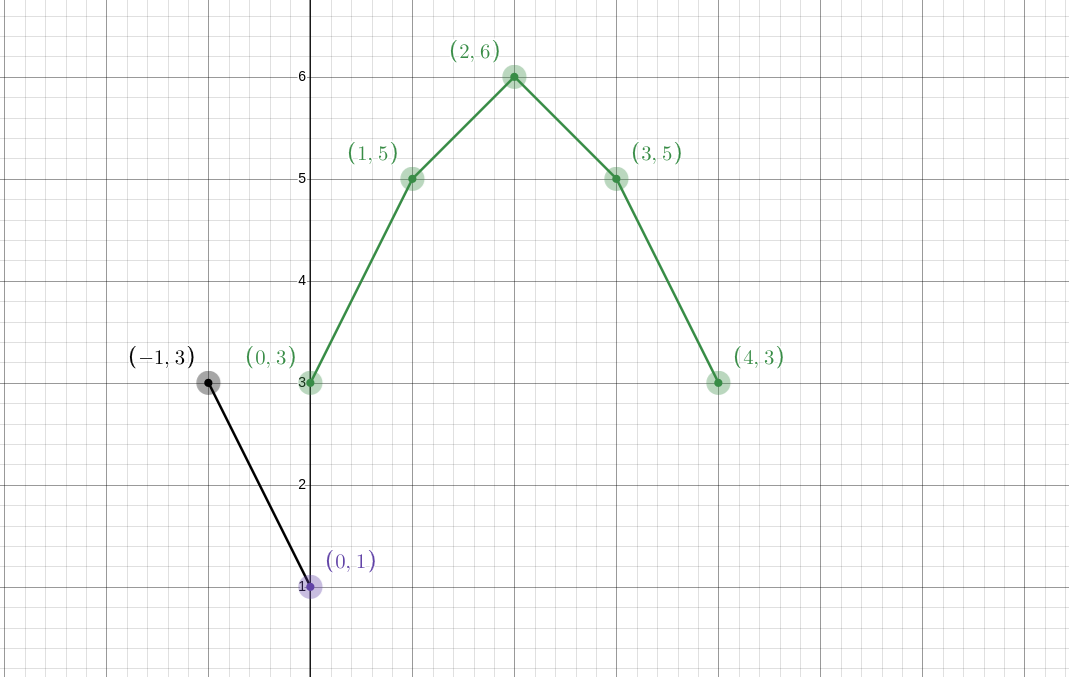
然后你就建完啦。

那么会了闵可夫斯基和能干什么呢？可以看到他就是用来快速的求两个向量集合相加后的凸包的，那么我们考虑分治，对于区间 $ [l,r] $ ，每次我们解决跨过中点的那些区间，即 $ pre_r - pre_l , r \gt mid , l \le mid $ ，其中 $ pre_i $ 表示前缀和，这可以看做是两个向量集合相加的形式，于是我们可以 $ O(n) $ 的去解决分支的每一层，那么时间复杂度到这是 $ O(n \log n) $ 的，然后考虑维护了每个小凸包后我们应该把他们合成一个大凸包，如果实时合并的话需要二分，是 $ O (n \log ^2 n) $ 的，如果最后排序维护凸包的话也是 $ O (n \log ^2 n) $ 的，以及询问也需要 $ O ( q \log n ) $ 的，所以总时间复杂度为 $ O ( n \log ^2 n + q \log n ) $ 。

对了还有一些细节，比如特判 0 之类的，请自己斟酌。

码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define int ll
typedef unsigned long long ull;
typedef pair<int,int> pii;
#define fi first
#define se second
#define mk make_pair
#define ps push_back
const int N=1e6+10,inf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f,mod=1e9+7;
inline ll read(){
	char c=getchar();ll x=0;bool f=0;
	while(!isdigit(c))f=c=='-'?1:0,c=getchar();
	while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return f?-x:x;
}
int n,a[N],b[N],Q;
pii pre[N],pre2[N];
inline pii operator + (const pii&x,const pii&y){return {x.fi+y.fi,x.se+y.se};}
inline pii operator - (const pii&x){return {-x.fi,-x.se};}
pii q1[N],q2[N],q[N],tp[N];
int q1l,q1r,q2l,q2r,qql,qqr;
vector<pii> v;
inline void sol1(int l,int r){
	if(l==r)return;
	int mid=l+r>>1;
	sol1(l,mid),sol1(mid+1,r);
	q1l=1;q1r=0;
	for(int i=l;i<=mid;++i){
		if(i!=l&&pre2[i].fi==pre2[i-1].fi)continue;
		while(q1l<q1r&&(q1[q1r].se-q1[q1r-1].se)/(double)(q1[q1r].fi-q1[q1r-1].fi)<=(pre2[i].se-q1[q1r].se)/(double)(pre2[i].fi-q1[q1r].fi))--q1r;
		q1[++q1r]=pre2[i];
	}
	q2l=1;q2r=0;
	for(int i=mid+1;i<=r;++i){
		if(i!=mid+1&&pre[i].fi==pre[i-1].fi)continue;
		while(q2l<q2r&&(q2[q2r].se-q2[q2r-1].se)/(double)(q2[q2r].fi-q2[q2r-1].fi)<=(pre[i].se-q2[q2r].se)/(double)(pre[i].fi-q2[q2r].fi))--q2r;
		q2[++q2r]=pre[i];
	}
	qql=1,qqr=0;q[++qqr]=q1[1]+q2[1];
	while(q1l<q1r&&q2l<q2r){
		if((q1[q1l+1].se-q1[q1l].se)/(double)(q1[q1l+1].fi-q1[q1l].fi)>=(q2[q2l+1].se-q2[q2l].se)/(double)(q2[q2l+1].fi-q2[q2l].fi))q[qqr+1]=q[qqr]+q1[q1l+1]+(-q1[q1l]),++qqr,++q1l;
		else q[qqr+1]=q[qqr]+q2[q2l+1]+(-q2[q2l]),++qqr,++q2l;
	}
	while(q1l<q1r)q[qqr+1]=q[qqr]+q1[q1l+1]+(-q1[q1l]),++qqr,++q1l;
	while(q2l<q2r)q[qqr+1]=q[qqr]+q2[q2l+1]+(-q2[q2l]),++qqr,++q2l;
	while(qql<=qqr)v.ps(q[qql++]);
	int i=l,j=mid+1,k=l;
	while(i<=mid&&j<=r){
		if(pre2[i].fi<pre2[j].fi||(pre2[i].fi==pre2[j].fi&&pre2[i].se>=pre2[j].se))tp[k++]=pre2[i++];
		else tp[k++]=pre2[j++];
	}
	while(i<=mid)tp[k++]=pre2[i++];
	while(j<=r)tp[k++]=pre2[j++];
	for(int i=l;i<=r;++i)pre2[i]=tp[i];
	for(int i=l;i<=r;++i)pre[i]=-pre2[r-(i-l)];
}
inline void sol2(int l,int r){
	if(l==r)return;int mid=l+r>>1;
	sol2(l,mid),sol2(mid+1,r);q1l=1;q1r=0;
	for(int i=l;i<=mid;++i){
		if(i!=l&&pre2[i].fi==pre2[i-1].fi)continue;
		while(q1l<q1r&&(q1[q1r].se-q1[q1r-1].se)/(double)(q1[q1r].fi-q1[q1r-1].fi)>=(pre2[i].se-q1[q1r].se)/(double)(pre2[i].fi-q1[q1r].fi))--q1r;
		q1[++q1r]=pre2[i];
	}
	q2l=1;q2r=0;
	for(int i=mid+1;i<=r;++i){
		if(i!=mid+1&&pre[i].fi==pre[i-1].fi)continue;
		while(q2l<q2r&&(q2[q2r].se-q2[q2r-1].se)/(double)(q2[q2r].fi-q2[q2r-1].fi)>=(pre[i].se-q2[q2r].se)/(double)(pre[i].fi-q2[q2r].fi))--q2r;
		q2[++q2r]=pre[i];
	}
	qql=1,qqr=0;
	q[++qqr]=q1[1]+q2[1];
	while(q1l<q1r&&q2l<q2r){
		if((q1[q1l+1].se-q1[q1l].se)/(double)(q1[q1l+1].fi-q1[q1l].fi)<=(q2[q2l+1].se-q2[q2l].se)/(double)(q2[q2l+1].fi-q2[q2l].fi))q[qqr+1]=q[qqr]+q1[q1l+1]+(-q1[q1l]),++qqr,++q1l;
		else q[qqr+1]=q[qqr]+q2[q2l+1]+(-q2[q2l]),++qqr,++q2l;
	}
	while(q1l<q1r)q[qqr+1]=q[qqr]+q1[q1l+1]+(-q1[q1l]),++qqr,++q1l;
	while(q2l<q2r)q[qqr+1]=q[qqr]+q2[q2l+1]+(-q2[q2l]),++qqr,++q2l;
	while(qql<=qqr)v.ps(q[qql++]);
	int i=l,j=mid+1,k=l;
	while(i<=mid&&j<=r){
		if(pre2[i].fi<pre2[j].fi||(pre2[i].fi==pre2[j].fi&&pre2[i].se<=pre2[j].se))tp[k++]=pre2[i++];
		else tp[k++]=pre2[j++];
	}
	while(i<=mid)tp[k++]=pre2[i++];
	while(j<=r)tp[k++]=pre2[j++];
	for(int i=l;i<=r;++i)pre2[i]=tp[i];
	for(int i=l;i<=r;++i)pre[i]=-pre2[r-(i-l)];
}
struct A{
	int x,y,id;
}QQ[N];
int ans[N],man[N];
signed main(){

	// #ifndef ONLINE_JUDGE
	freopen("cross.in","r",stdin);
	freopen("cross.out","w",stdout);
	// #endif
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	n=read();Q=read();
	for(int i=1;i<=n;++i)a[i]=read(),b[i]=read(),pre[i]=pre[i-1]+pii{a[i],b[i]},pre2[i]=pre2[i-1]+(-pii{a[i],b[i]});
	for(int i=1;i<=Q;++i)QQ[i].x=read(),QQ[i].y=read(),QQ[i].id=i;
	sol1(0,n);sort(v.begin(), v.end(),[](const pii&x,const pii&y){return x.fi==y.fi?x.se>y.se:x.fi<y.fi;});
	qql=1,qqr=0;
	for(auto i:v){
		if(qqr&&i.fi==q[qqr].fi)continue;
		while(qql<qqr&&(q[qqr].se-q[qqr-1].se)/(double)(q[qqr].fi-q[qqr-1].fi)<=(i.se-q[qqr].se)/(double)(i.fi-q[qqr].fi))--qqr;
		q[++qqr]=i;
	}
	sort(QQ+1,QQ+1+Q,[](const A&x,const A&y){return (x.x==0?-1e18:(double)x.y/x.x)>(y.x==0?-1e18:(double)y.y/y.x);});
	for(int i=1;i<=Q;++i){
		if(QQ[i].x==0)break;
		while(qql<qqr&&(q[qql+1].se-q[qql].se)/(double)(q[qql+1].fi-q[qql].fi)>=(double)QQ[i].y/QQ[i].x)++qql;
		ans[QQ[i].id]=max(ans[QQ[i].id],QQ[i].x*q[qql].se-QQ[i].y*q[qql].fi);
	}
	pre[0]={0,0},pre2[0]={0,0};
	for(int i=1;i<=n;++i)pre[i]=pre[i-1]+pii{a[i],b[i]},pre2[i]=pre2[i-1]+(-pii{a[i],b[i]});
	v.clear();sol2(0,n);sort(v.begin(), v.end(),[](const pii&x,const pii&y){return x.fi==y.fi?x.se<y.se:x.fi<y.fi;});
	qql=1,qqr=0;
	for(auto i:v){
		if(qqr&&i.fi==q[qqr].fi)continue;
		while(qql<qqr&&(q[qqr].se-q[qqr-1].se)/(double)(q[qqr].fi-q[qqr-1].fi)>=(i.se-q[qqr].se)/(double)(i.fi-q[qqr].fi))--qqr;
		q[++qqr]=i;
	}
	sort(QQ+1,QQ+1+Q,[](const A&x,const A&y){return (x.x==0?1e18:(double)x.y/x.x)<(y.x==0?1e18:(double)y.y/y.x);});
	for(int i=1;i<=Q;++i){
		if(QQ[i].x==0)break;
		while(qql<qqr&&(q[qql+1].se-q[qql].se)/(double)(q[qql+1].fi-q[qql].fi)<=(double)QQ[i].y/QQ[i].x)++qql;
		ans[QQ[i].id]=max(ans[QQ[i].id],QQ[i].x*q[qql].se-QQ[i].y*q[qql].fi);
	}
	int i1=0,i2=0,man1=linf,man2=-linf;
	for(int i=1;i<=n;++i){
		i1+=a[i],i2+=a[i];
		man1=min(man1,i1),man2=max(man2,i2);
		if(i1>0)i1=0;if(i2<0)i2=0;
	}
	for(int i=1;i<=Q;++i){
		if(QQ[i].x==0){
			if(QQ[i].y<=0)ans[QQ[i].id]=max(ans[QQ[i].id],-man2*QQ[i].y);
			else ans[QQ[i].id]=max(ans[QQ[i].id],-man1*QQ[i].y);
		}
	}
	for(int i=1;i<=Q;++i)
		cout<<ans[i]<<'\n';
}

T3、序列变换

不会，run了

\[return \ \ 0 \]

posted @ 2025-01-10 10:04 lzrG23 阅读(50) 评论(0) 收藏举报

刷新页面返回顶部

GGrun-sum

2025多校冲刺省选模拟赛3

2025多校冲刺省选模拟赛3

T1、等差

T2、叉积

T3、序列变换

公告

GGrun-sum

2025多校冲刺省选模拟赛3

2025多校冲刺省选模拟赛3

T1、 等差

T2、 叉积

T3、 序列变换

公告

T1、等差

T2、叉积

T3、序列变换