CSP模拟 小 trick 总结 (持续施工中)
虽然这篇博客来的有点晚,但还是写了,欢迎dalao补充(
(很杂,建议先浏览目录)
1、分块、莫队有关:
\(\color{brown}(1)一个真正的回滚莫队(感谢\ Qyun\ 的讲解):\)
$\ \ \ \ \ \ \ \ $学习回滚莫队的时候,我们经常会在回滚时使用memcpy来恢复以前的版本,但众所周知--memset和memcpy常数巨大,破坏了莫队 $ O(n \sqrt n) $ 的时间复杂度,导致TLE。
$\ \ \ \ \ \ \ \ $但对于一些可以进行del操作,只是不好改变答案的回滚(比如求一个区间的众数),直接记下来回滚版本的ans,然后进行del操作,因为块长为 $ \sqrt n $ ,所以每次最多进行 $ \sqrt n $ 次操作,总时间复杂度$ O(n \sqrt n) $
----例题:洛谷 P3709
MAN
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
#define fi first
#define se second
#define ps push_back
#define mk make_pair
#define rint register int
#define G cout<<"-------------------"<<endl
inline ll read(){
char c=getchar();ll x=0,f=1;
while(!isdigit(c))(c=='-'?f=-1:0),c=getchar();
while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
const int N=2e5+3,inf=0x7fffffff;
const ll linf=0x3f7f7f7f7f7f7f7f,mod=1e9+7;
int n,a[N],cnt[N],b[N],ans,anss[N],m,zh[N],cntp,len,st[N],ed[N];
struct jj{
int l,r,id;
inline bool operator <(const jj&x)const{
if(zh[l]==zh[x.l])return r<x.r;
return zh[l]<zh[x.l];
}
}q[N];
int main(){
// #ifndef ONLINE_JUDGE
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
// #endif
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
n=read(),m=read();
len=pow(n,0.5),cntp=n/len;
for(int i=1;i<=cntp;++i){
st[i]=ed[i-1]+1,ed[i]=ed[i-1]+len,ed[cntp]=n;
for(int j=st[i];j<=ed[i];++j)
zh[j]=i;
}
for(int i=1;i<=n;++i)
b[i]=a[i]=read();
sort(b+1,b+1+n);
int n1=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=n;++i)
a[i]=lower_bound(b+1,b+1+n1,a[i])-b;
for(int i=1,l,r;i<=m;++i){
l=read(),r=read();q[i]={l,r,i};
}
sort(q+1,q+1+m);
int l1=0,r1=0;int la=0;
for(int i=1,l,r;i<=m;++i){
// cout<<i<<endl;/
l=q[i].l,r=q[i].r;
if(zh[l]==zh[r]){
fill(cnt+1,cnt+1+n1,0);ans=0;
for(int j=l;j<=r;++j)
ans=max(ans,++cnt[a[j]]);
anss[q[i].id]=ans;
continue;
}
if(zh[l]!=zh[q[i-1].l]||zh[q[i-1].l]==zh[q[i-1].r]){
fill(cnt+1,cnt+1+n1,0);
l1=ed[zh[l]],r1=l1-1;ans=la=0;
}
while(r1<r)ans=max(ans,++cnt[a[++r1]]);
// memcpy(zan,cnt,4*(n1+1));
la=ans;
while(l1>l)ans=max(ans,++cnt[a[--l1]]);
anss[q[i].id]=ans;
ans=la;while(l1<ed[zh[l]])--cnt[a[l1++]];
}
for(int i=1;i<=m;++i)
cout<<-anss[i]<<'\n';
}
2、分治有关:
\(\color{brown}(1) CDQ分治:\)
CDQ 初学的话推荐一个博客:mlystdcall
$\ \ \ \ \ \ \ \ $ cdq分治可以解决很多高维偏序问题,例如:给了 a,b,c 三维,有 $a_i \lt a_j,b_i \lt b_j , c_i \lt c_j $ 的限制条件的问题,如果出题人不是 毒瘤 ,可以离线的话,那么就可以用cdq, $ O(n\ log^2 n)$轧过这道题。
$\ \ \ \ \ \ \ \ $ 1、CDQ 优化 DP:
$\ \ \ \ \ \ \ \ $ LIS是一个非常典型的线性DP,他的转移限制条件是 $ v_i \ge v_j $ .
$\ \ \ \ \ \ \ \ $ 那如果在一个高维问题中,他有很多维限制条件呢?
$\ \ \ \ \ \ \ \ $ -----例题:洛谷P5621
$\ \ \ \ \ \ \ \ $ 看上去就是个四维CDQ分治,但是这个CDQ并不太好写,我们在进行CDQ分治时,是计算左边对右边的贡献,像求一个矩阵内有多少点的这种贡献是可以直接累加的,但这道题的DP的转移 $$\Huge f_i = \max_{a_i \ge a_j , b_i \ge b_j , c_i \ge c_j , d_i \ge d_j} f_j + v_i$$
$\ \ \ \ \ \ \ \ $ 按照一般的CDQ过程,我们是先处理左区间、右区间,再计算左区间对右区间的贡献的 ->:
inline void cdq(int l,int r){
if(l==r)return;
int mid=l+r>>1;
cdq(l,mid),cdq(mid+1,r);
/*
luangao
*/
}
$\ \ \ \ \ \ \ \ $ 画成图的话就是:
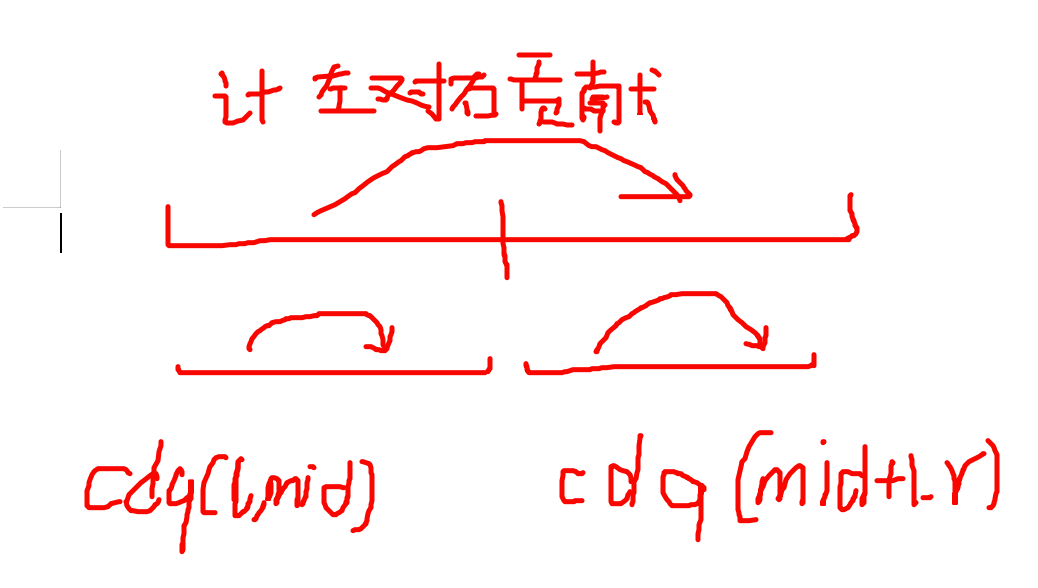
$\ \ \ \ \ \ \ \ $ 但是这样我们就无法将 左区间 对 右区间的右区间 和 右区间的左区间 对 右区间的右区间 的贡献统计在一起,举个例子,有几个全部相等的崩坏兽,那么我们可以获得全部贡献,但是用CDQ来计算的话,我们先解决了左区间,最多只获得了一半的贡献,然后又解决了右区间,最多获得一半贡献,然后再用左区间更新右区间,最多只有一半加一的贡献,导致最终答案少了 一部分贡献没有计算上。
$\ \ \ \ \ \ \ \ $ 既然先下放在计算会丢失贡献,那么我们可以先计算左区间,用左区间去更新一遍右区间,将左区间的贡献累加到右区间上,然后在下放到右区间去递归处理 ->
inline void cdq(int l,int r){
if(l==r)return;
int mid=l+r>>1;
cdq(l,mid);
sort(q+l,q+mid+1,cmp);sort(q+mid+1,q+r+1,cmp);//别忘了进行排序
/*
luangao
*/
cdq(mid+1,r);
}
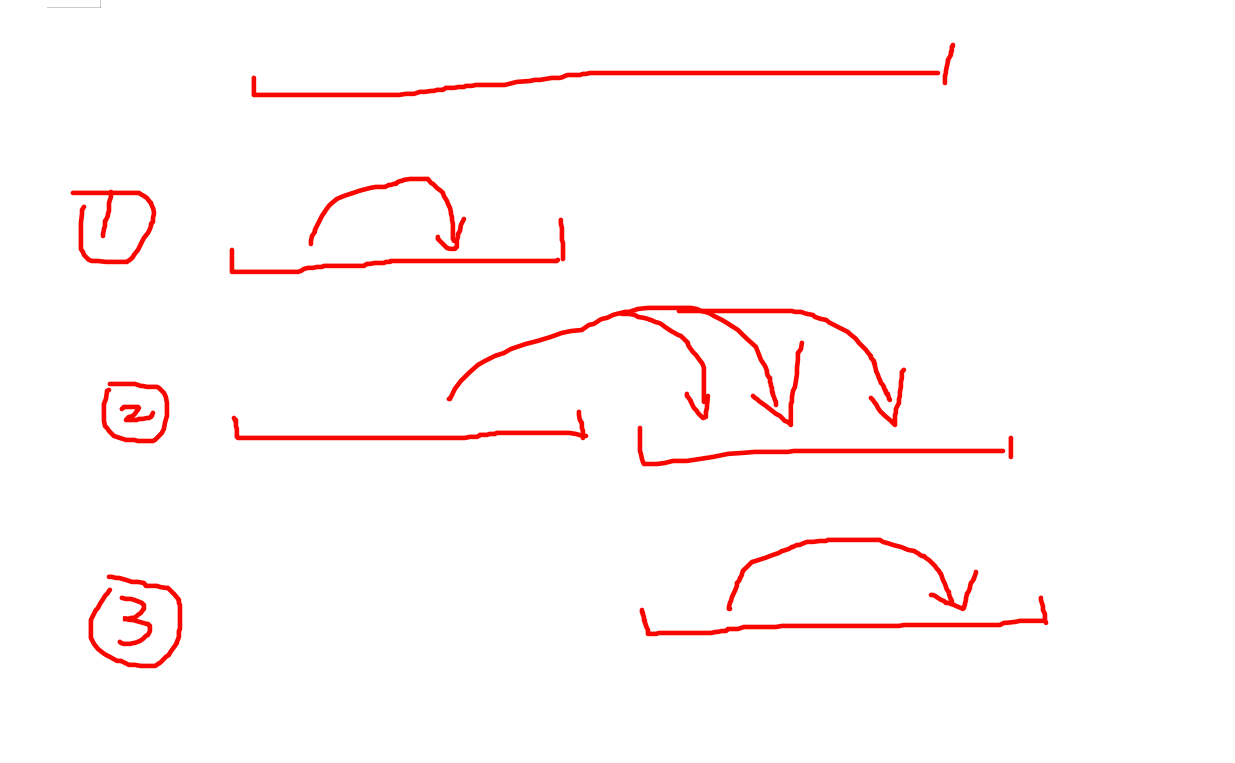
$\ \ \ \ \ \ \ \ $ 这样就不会丢失贡献了,不需要手写归并排序了,但一定要记得按某个关键字排好序再计算贡献!
P5621
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
#define fi first
#define se second
#define ps push_back
#define mk make_pair
#define rint register int
#define G cout<<"-------------------"<<endl
inline ll read(){
char c=getchar();ll x=0,f=1;
while(!isdigit(c))(c=='-'?f=-1:0),c=getchar();
while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
#define int ll
const int N=1e6+10,inf=0x7fffffff,B=1e5+1,BB=B<<1;
const ll linf=0x3f7f7f7f7f7f7f7f,mod=1e9+7;
ll f[N],w[N];
int n;
struct BIT{
ll c[BB];
inline void add(int x,ll y){
while(x<BB)
c[x]=max(c[x],y),x+=x&-x;
}
inline ll ask(int x){
ll ans=-linf;
while(x)
ans=max(ans,c[x]),x^=x&-x;
return ans;
}
inline void clear(int x){
while(x<BB)
c[x]=-linf,x+=x&-x;
}
}T;
struct jj{
int a,b,c,d,op,id;
}q[N],tp[N],tpp[N];
inline bool cmpb(const jj&x,const jj&y){
if(x.b!=y.b)return x.b<y.b;
if(x.c!=y.c)return x.c<y.c;
if(x.d!=y.d)return x.d<y.d;
if(x.a!=y.a)return x.a<y.a;
return w[x.id]>w[y.id];
}
inline bool cmpa(const jj&x,const jj&y){
if(x.a!=y.a)return x.a<y.a;
if(x.b!=y.b)return x.b<y.b;
if(x.c!=y.c)return x.c<y.c;
if(x.d!=y.d)return x.d<y.d;
return w[x.id]>w[y.id];
}
inline bool cmpc(const jj&x,const jj&y){
if(x.c!=y.c)return x.c<y.c;
if(x.d!=y.d)return x.d<y.d;
if(x.a!=y.a)return x.a<y.a;
if(x.b!=y.b)return x.b<y.b;
return w[x.id]>w[y.id];
}
inline void man(int l,int r){
if(l==r)return;
int mid=l+r>>1;
man(l,mid);
for(int i=l;i<=r;++i)
tpp[i]=tp[i];
stable_sort(tpp+l,tpp+mid+1,cmpc);
stable_sort(tpp+mid+1,tpp+r+1,cmpc);
for(int j=mid+1,i=l;j<=r;++j){
while(i<=mid&&tpp[i].c<=tpp[j].c){
if(!tpp[i].op)T.add(tpp[i].d,f[tpp[i].id]);
++i;
}
if(tpp[j].op)f[tpp[j].id]=max(f[tpp[j].id],T.ask(tpp[j].d)+w[tpp[j].id]);
}
for(int i=l;i<=mid;++i)
T.clear(tpp[i].d);
man(mid+1,r);
}
inline void cdq(int l,int r){
if(l==r)return;
int mid=l+r>>1;
cdq(l,mid);
for(int i=l;i<=r;++i)
tp[i]=q[i],tp[i].op=(i>mid);
stable_sort(tp+l,tp+r+1,cmpb);
man(l,r);
cdq(mid+1,r);
}
main(){
#ifndef ONLINE_JUDGE
freopen("in.in","r",stdin);
freopen("out.out","w",stdout);
#endif
ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
n=read();
memset(T.c,0xcf,sizeof(T.c));
for(int i=1,a,b,c,d,z;i<=n;++i){
a=read()+B,b=read()+B,c=read()+B,d=read()+B,z=read();q[i]={a,b,c,d,0,i};f[i]=z;w[i]=z;
}
stable_sort(q+1,q+1+n,cmpa);
cdq(1,n);
for(int i=2;i<=n;++i)
f[1]=max(f[1],f[i]);
cout<<f[1];
}
$\ \ \ \ \ \ \ \ $ 2、CDQ 排序:
$\ \ \ \ \ \ \ \ $ 如果你刷了几道 CDQ 的题,就会发现自己很可能会被排序卡死几个点,反正我是被卡死过很多次。
$\ \ \ \ \ \ \ \ $ 就拿上面的那道四维偏序DP来说,光cmp函数就有三个,写的时候也是很恶心,那为什么会出错呢?
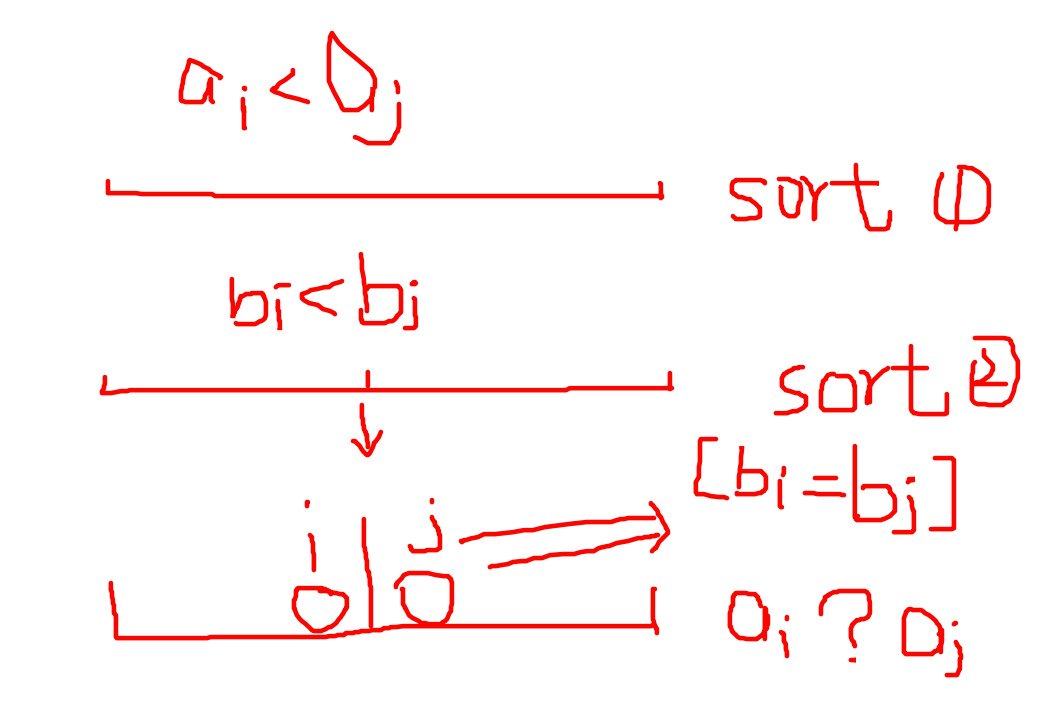
$\ \ \ \ \ \ \ \ $ 我们先将数组以 $ a $ 为关键字进行了排序,然后给左边打上 $ L $ 的标记,给右边打上 $ R $ 的标记,然后再以 $ b $ 为关键字进行排序,但是如果只按 $ b $ 为关键字的话,可能在中间有两个元素的 $ b $ 值是相等的,但用sort会使两者随机分配到两边,那么就有可能造成 $ a_i > a_j $ 的情况,从而导致原本 $ j $ 可以对 $ i $ 的贡献消失了,也就导致最终的答案出错。
$\ \ \ \ \ \ \ \ $ 为了避免这种情况的出现,我们最好用上所有可能对答案造成影响的关键字进行排序,根据当前的需求确定第一、第二等关键字,然后再sort。
$\ \ \ \ \ \ \ \ $ 还有一种较为简便的,可以使用 $ stable _ \ sort $,这两者的区别就在于 \(sort\) 在比较两个完全一样的元素时,是分配的随机位置,而 $ stable _\ sort$ 则是按照原序列的位置不变,不过 $ stable _ \ sort$ 略慢于 $ sort $ 。
3、最短路及其优化:
\(\color{brown} \ \ \ \ \ \ \ \ \ (1)堆优化dijkstra \ 小优化:\) (感谢 $ wlesq $ 帮忙指出错误,提出建议)
$\ \ \ \ \ \ \ \ $ 可能与大家不太一样,反正我一开始写 堆优化的 $ dijkstra $ 时,总是会把整个 $ priority _\ queue $ 给 pop 完才结束,这就会造成大量的冗余运算,及其地浪费时间,但是根据 $ dijkstra $ 的贪心原理,vis 被标记的点,他的答案已经确定了,而且也没有更新的价值了,所以直接 continue 掉就好了。还有每次有效的 \(top\) 值都会确定一个点的 \(dis\) 值,那么有效的取 $ top $ 值只会有 $ n $ 次,所以我们只进行 $n $ 次有效的取 $ top $ 值就行了(当然你得保证他能取 n 次,即保证图是联通的,需要判一下 \(priority\_\ queue\) 不空)。
$\large码$
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
#define fi first
#define se second
#define ps push_back
#define mk make_pair
#define rint register int
#define G cout<<"-------------------"<<endl
inline ll read(){
char c=getchar();ll x=0,f=1;
while(!isdigit(c))(c=='-'?f=-1:0),c=getchar();
while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
const int N=2e5+10,inf=0x7fffffff;
const ll linf=0x3f7f7f7f7f7f7f7f,mod=1e9+7;
ll v[N];
ll n,hd[N],cnt,m,dis[N];
struct jj{
int fr,to,next;ll w;
}bi[N<<1];
inline void add(int x,int y,ll z){
bi[++cnt]={x,y,hd[x],z+v[y]},hd[x]=cnt;
bi[++cnt]={y,x,hd[y],z+v[x]},hd[y]=cnt;
}
bool vis[N];
signed main(){
#ifndef ONLINE_JUDGE
freopen("in.in","r",stdin);
freopen("out.out","w",stdout);
#endif
n=read(),m=read();
for(int i=1;i<=n;++i)
v[i]=read();
ll x,y,z;
for(int i=1;i<=m;++i){
x=read(),y=read(),z=read();
add(x,y,z);
}
memset(dis,0x3f,sizeof(dis));
priority_queue<pair<ll,int> >q;
dis[1]=0;q.push({0,1});
for(int p=1;p<=n&&!q.empty();++p){
int k=q.top().se;q.pop();
if(vis[k]){//无效的取值
--p;continue;
}
vis[k]=1;
for(int i=hd[k];i;i=bi[i].next){
int j=bi[i].to;
if(vis[j])continue;
if(dis[j]>dis[k]+bi[i].w){
dis[j]=dis[k]+bi[i].w,q.push({-dis[j],j});
}
}
}
for(int i=2;i<=n;++i)
printf("%lld ",dis[i]+v[1]);
}
$\ \ \ \ \ \ \ \ $ 还有给大家看一下他的优化效果:

\(\ \ \ \ \ \ \ \ \ \color{brown}(2)求定点最小环:\)
$\ \ \ \ \ \ \ \ $ 先看题面:

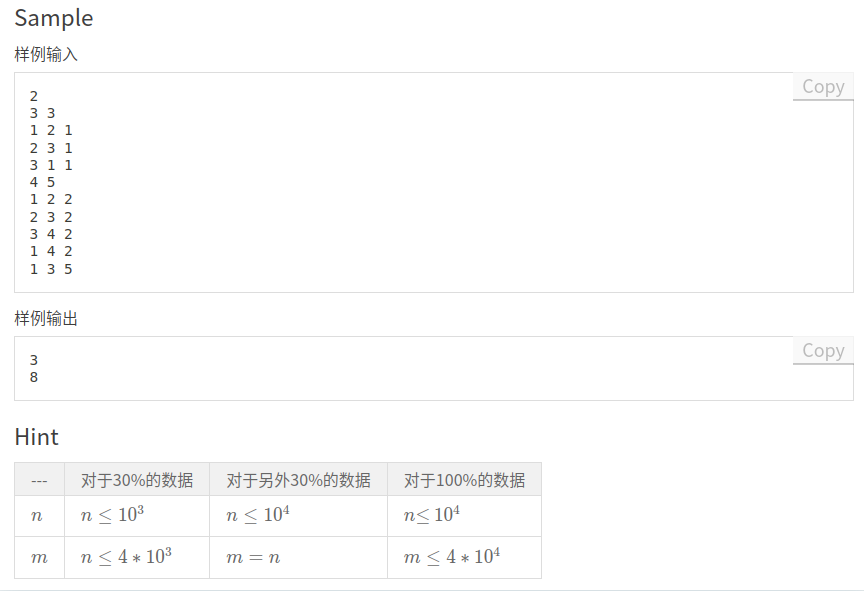
$\ \ \ \ \ \ \ \ $ 集训时的考试题,先讲一下正解:
$\ \ \ \ \ \ \ \ $ 考虑把一个环拆开,那么一个最短环一定是由 1 向两个点的最短路加上这两个点不经过 1 这个点的最短路加和起来所得的。
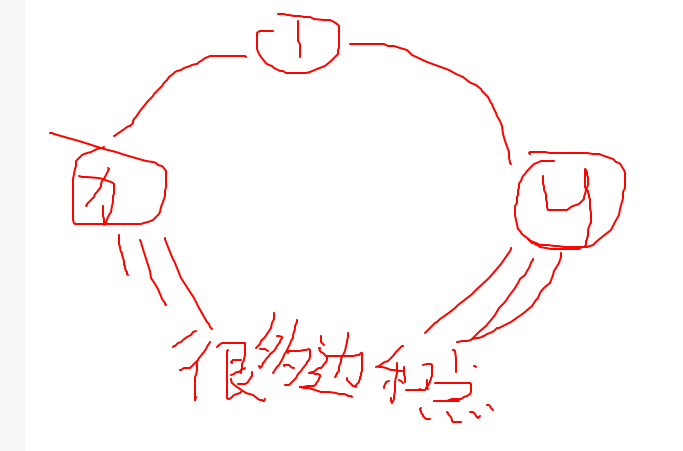
$\ \ \ \ \ \ \ \ $ 那么一个暴力的做法就是找出 1 能直接连通的所有点,放在 $ S $ 这个集合里面,两两之间枚举以某一个点为起点,删去经过 1 的边,然后跑一边 dij ,时间 $ O(nm \ log\ n) $ 。为啥会 T 呢,因为他有很多的冗杂运算,以两个不同的点为起点来跑 dij 的过程中有很多计算都是相同的,那么我们考虑怎么去减少跑最短路的次数,也就要学习一下二进制分组建图来压缩计算次数。
$\ \ \ \ \ \ \ \ $ 本质上来讲,我们就是通过找出所有 $ S $ 里面的每对点的最短路来求解,那么只要枚举了所有的点对就行,然后我们知道: $$ 任意两个不同的数,在二进制表达式上,一定有一位不同 $$
$\ \ \ \ \ \ \ \ $ 那么我们就可以利用这个性质,利用二进制将他们分组:具体来说,就是枚举二进制的每一位, 0 为一组,分到集合 $ S1 $, 1 为一组,分到集合 $ S2 $,建立两个虚点 d1,d2,一个作为起点,将 1 到 $ S1 $ 内的点的单向边转移为 d1 向 $ S1 $ 中的点的连边,另一个作为终点,将 $ S2 $ 中的点向 1 的连边转移为 $ S2 $ 中的点向 d2 连边,然后抛弃所有与 1 有关的边,从 d1 跑一条最短路即可,只需要跑 $ log n $ 次。

$\ \ \ \ \ \ \ \ $ 因为每两个数必有一位在二进制上不同,所以我么一定枚举了所有的点对,也就包含了所有的情况。
没有打码,粘个雪张的过来
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<cmath>
inline int read(){
int x=0,fh=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=2e5+5;
int t,head[maxn],tot=2,n,m,cnt,qd,zd;
struct asd{
int to,next,val;
}b[maxn];
void ad(int aa,int bb,int cc){
b[tot].to=bb;
b[tot].next=head[aa];
b[tot].val=cc;
head[aa]=tot++;
}
struct jie{
int num,jl;
jie(){}
jie(int aa,int bb){
num=aa,jl=bb;
}
bool operator < (const jie& A)const{
return jl>A.jl;
}
};
bool vis[maxn];
int dis[maxn];
void dij(int qd){
std::priority_queue<jie> q;
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[qd]=0;
q.push(jie(qd,0));
while(!q.empty()){
int now=q.top().num;
q.pop();
if(now==zd) return;
if(vis[now]) continue;
vis[now]=1;
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(dis[u]>dis[now]+b[i].val){
dis[u]=dis[now]+b[i].val;
q.push(jie(u,dis[u]));
}
}
}
}
struct jl{
int bh,jz;
jl(){}
jl(int aa,int bb){
bh=aa,jz=bb;
}
}c[maxn];
int main(){
freopen("leave.in","r",stdin);
freopen("leave.out","w",stdout);
t=read();
while(t--){
memset(head,-1,sizeof(head));
memset(&b,0,sizeof(b));
memset(&c,0,sizeof(c));
tot=2,cnt=0;
n=read(),m=read();
for(int i=1;i<=m;i++){
int aa,bb,cc;
aa=read(),bb=read(),cc=read();
if(aa>bb) std::swap(aa,bb);
if(aa==1) c[++cnt]=jl(bb,cc);
else {
ad(aa,bb,cc);
ad(bb,aa,cc);
}
}
int nans=0x3f3f3f3f,nn=n;
for(int i=1;i<=n;i<<=1){
qd=++nn,zd=++nn;
for(int j=1;j<=cnt;j++){
if(c[j].bh&i) ad(qd,c[j].bh,c[j].jz);
else ad(c[j].bh,zd,c[j].jz);
}
dij(qd);
nans=std::min(nans,dis[zd]);
}
if(nans==0x3f3f3f3f) printf("-1\n");
else printf("%d\n",nans);
}
return 0;
}
$\ \ \ \ \ \ \ \ $ 没有打码的原因是因为考场上糊了另外一个爆改版 $ dij $ ,还跑过了,大概就是,先给 1 dis值赋为﹢∞ ,将其直接相连的点赋为对应边的边权,以每条最短路的起始边(与1相连的边)为源边,只需跑最短路记录每个点的最短路的源边,并找到不通过这条源边的最短路(合法的次短路),然后将它们俩合并就行,最后 ans 和 $ dis_1 $ 取 min 即可。(其实我不确定这么做是对的 ~
给了一些注释
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
typedef unsigned long long ull;
#define fi first
#define se second
#define ps push_back
#define mk make_pair
#define rint register int
#define G cout<<"-------------------"<<endl
inline ll read(){
char c=getchar();ll x=0,f=1;
while(!isdigit(c))(c=='-'?f=-1:0),c=getchar();
while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
const int N=1e6+10,inf=0x3f3f3f3f;
const ll linf=0x3f7f7f7f7f7f7f7f,mod=1e9+7;
int n,m,cnt,hd[N],disp[N];
struct jj{
int to,next,w;
}bi[N];
pii dis[N];
bool vis[N];
inline void add(int x,int y,int z){bi[++cnt]={y,hd[x],z},hd[x]=cnt,bi[++cnt]={x,hd[y],z},hd[y]=cnt;}
inline void dij(int x){
// G;G;G;
fill(dis+1,dis+1+n,mk(inf,0));//pair 类型的 dis,first存权值,second存源边
fill(disp+1,disp+1+n,inf);// 合法的(不走源边)的最短路
priority_queue<pair<pii,int> > q;
for(int i=hd[x];i;i=bi[i].next){
int j=bi[i].to;
dis[j].fi=min(dis[j].fi,bi[i].w);dis[j].se=i,q.push({{-dis[j].fi,dis[j].se},j});//将 1 的边权赋给各个点
}
while(!q.empty()){
int k=q.top().se;q.pop();
for(int i=hd[k];i;i=bi[i].next){
if(i==(dis[k].se^1))continue;// 和源边是一条边,不能走
int j=bi[i].to;
if(dis[j].fi>dis[k].fi+bi[i].w){// 更新最短路
dis[j]={dis[k].fi+bi[i].w,dis[k].se};q.push({{-dis[j].fi,dis[j].se},j});
}
if(dis[j].se!=dis[k].se){// 用最短路更新次短路
if(disp[j]>dis[k].fi+bi[i].w)
disp[j]=dis[k].fi+bi[i].w,q.push({{-dis[j].fi,dis[j].se},j});
}
if(disp[j]>disp[k]+bi[i].w)// 用次短路更新次短路
disp[j]=disp[k]+bi[i].w,q.push({{-dis[j].fi,dis[j].se},j});
}
}
int ans=1e9;
for(int i=hd[x];i;i=bi[i].next){
int j=bi[i].to;
ans=min(ans,disp[j]+dis[j].fi);
}
ans=min(ans,dis[x].fi);// 自己走到了 1 的最短路
cout<<(ans==1e9?-1:ans)<<'\n';
}
int main(){
// #ifndef ONLINE_JUDGE
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
// #endif
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=read();
while(t--){
n=read(),m=read();
fill(hd+1,hd+1+n,0);cnt=1;
for(int i=1,x,y,z;i<=m;++i){
x=read(),y=read(),z=read();
add(x,y,z);
}
// cout<<1<<endl;
dij(1);
}
}
4、杂项 trick
$\ \ \ \ \ \ \ \ $ (1)正难则反类:
$\ \ \ \ \ \ \ \ $ $ \color{brown} 1、对一颗树逐渐进行删边操作,并询问每个状态下距离点 u 的最远距离$
$\ \ \ \ \ \ \ \ $ 删边会导致答案变小,但加边只会让答案越来越大,所以把整个操作序列反过来改为加边操作,然后维护每棵树中的直径,以及直径的两端端点,同时有两条经典定理: $$ 一个点到最远点的一定是它到直径的某个端点的距离 $$
$\ \ \ \ \ \ \ \ $ (2)合理利用题目数据范围:
$\ \ \ \ \ \ \ \ $ 这类题目也不少,会有一个变量他的范围很小,那么这就是出题人留给我们的切入点,好好利用数据范围可以帮忙启发正解
$\ \ \ \ \ \ \ \ $ (3)异或哈希:
$\ \ \ \ \ \ \ \ $ 先看例题:

$\ \ \ \ \ \ \ \ $ 首先博弈的结论是比较容易得出的,也就是只要路径上有一种数的个数是奇数那么就先手必胜,所以我们只需要判断一个路径上是不是所有的数的个数都是偶数就行。那我们就可以考虑异或,如果所有的数的个数都是偶数的话,那么他们异或起来一定是 $ 0 $ ,但是即使不全都是偶数个,他们异或起来也有可能是 $ 0 $,比如 $ 1 \ xor \ 2 \ xor \ 3 = 0 $,这样数据是十分容易构造的,但是我们可以重组已经构造好的数,也就是通过哈希让他们映射到一些不容易发生冲突的数上去。即使正常哈希有被卡的可能,但我们甚至可以通过随机化将他们映射到一个自己也不确定的数上去,这样就几乎不会被卡了。比如可以这样映射:
map[x]=(ll)rand()+rand();
暂时只有这些,会持续施工。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号