题解：P14301 [JOI2023 预选赛 R2] 日本沉没 2 / Japan Sinks 2

P14301

我太菜了，这题花了我两天才写出来。

直接维护序列好像不是很好维护，但是我们可以考虑维护一下这个序列的轮廓，就是这个。

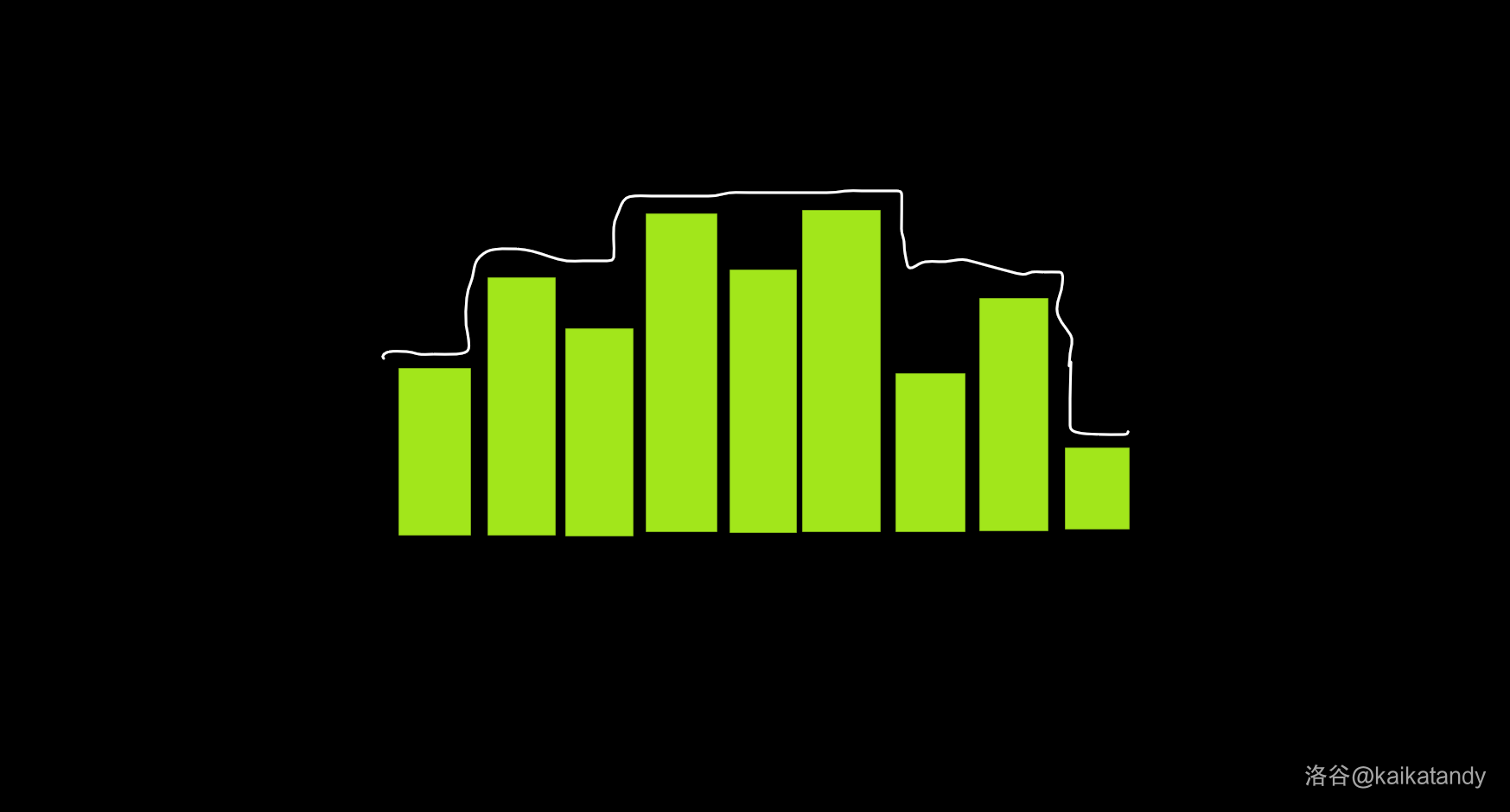
其实这玩意儿就是 \(\min(premax(i),sufmax(i))\)，我们暂且把它叫 \(f_i\)。

为什么要选择维护这东西呢？不难发现，查询的时候，答案就是 \(\min(f_i,a_i)\)（这里的 \(a_i\) 是初始值，以下都代表初始值），这非常方便。而且观察一下，修改也很方便，每一次修改都是一段前/后缀减一。以下只讨论西风的情况。

具体是哪一段前缀？观察发现，这个序列一直都呈现一个“山峰”的状态，并不会出现下凹的形状，于是肯定会有一段“山顶”，就是蓝色这一块。

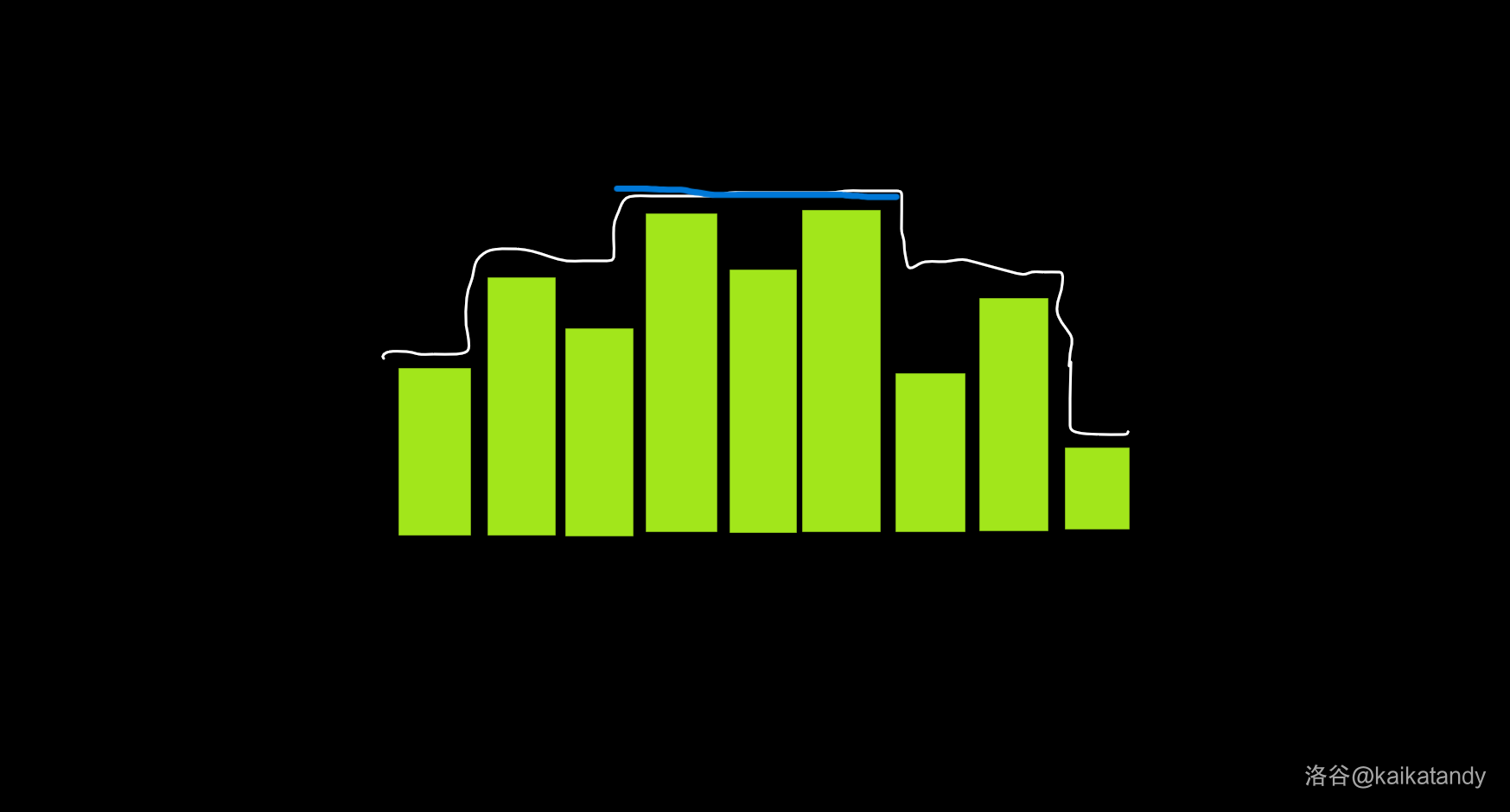
那么假设我们的操作是

1 x

，如果 \([1,x]\) 包含了山顶，也就是说 \(x\) 已经到山顶右端的话，那么只需要将 \(1\) 到山顶右端的值全部减一即可，即红色这一段。

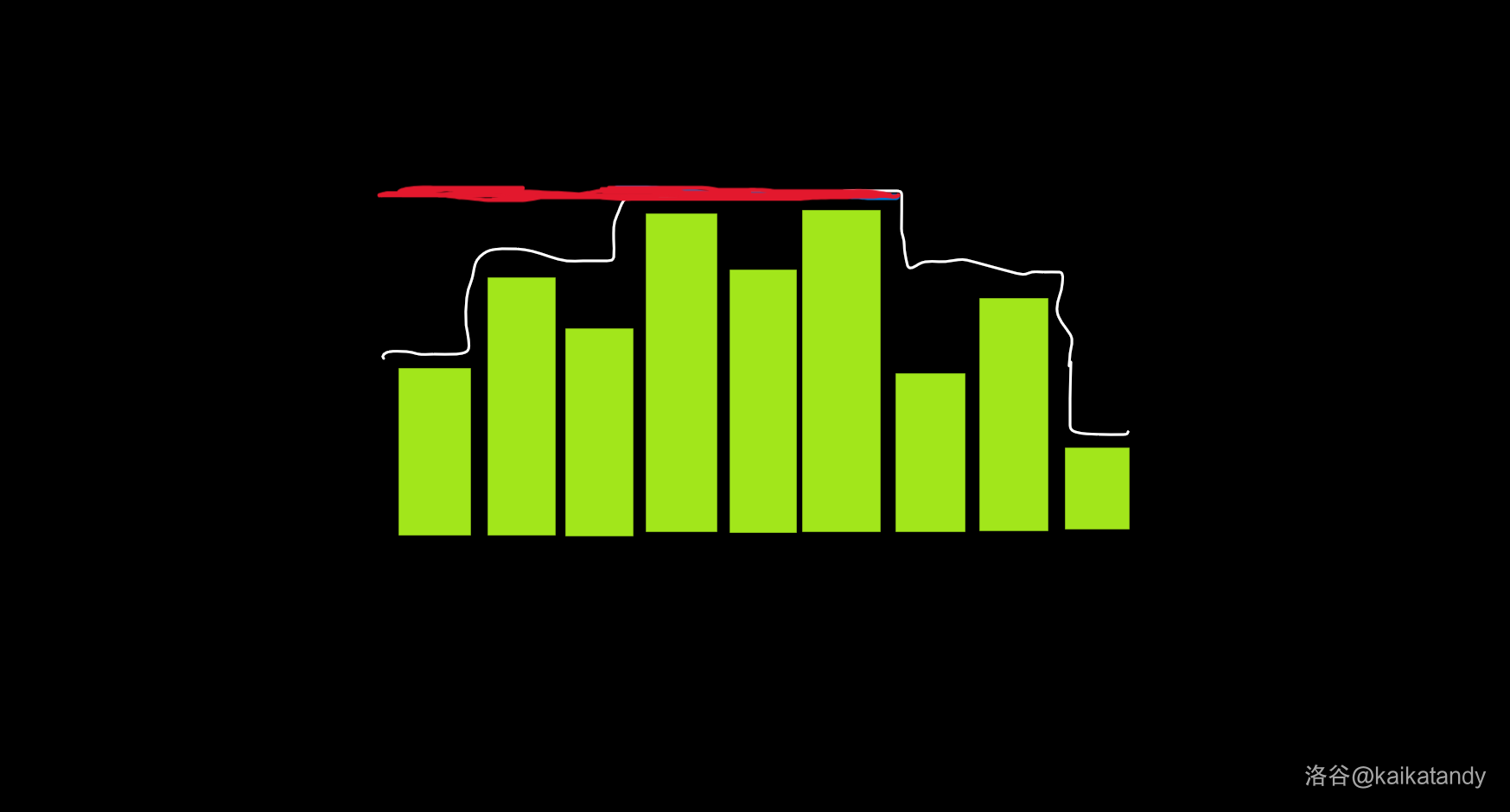
那么如果没有包括山顶？也就是 \(x\) 处于以上红线之内并且不在红线的右端的情况。这个时候，定义一个点是“突出的”，当且仅当 \(f_i-a_i\le 0\)。那么只需要找到 \(x\) 后面的第一个“突出的”点，将它前面的前缀减一即可。

就比如按照上面的图，\(x=2\) 时，它的下一个“突出的”点是 \(4\)，那么将 \([1,3]\) 全部减一即可。

东风同理。

现在解除前面的“只讨论西风”限制。 那么总结下线段树要实现什么功能：

• 区间加。
• 区间 \(\max(f_i)\)。
• 找到 \([1,n]\) 内最靠左/右的最大值（山顶的两端）。
• 找到一段区间内最靠左/右的 \(f_i-a_i\le 0\) 的下标。

维护的东西：

• \(\max(f_i)\)。
• \(\min(f_i-a_i)\)。
• 懒标记。

这不难在 \(\mathcal{O}(n\log^2n)\) 内实现。

//to kill a living book
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=3e5+7;
int n,pre[N],suf[N],a[N];
struct Misaka{
    #define ls (x<<1)
    #define rs (x<<1|1)
    #define mid (l+r>>1)
    int c[N<<2],f[N<<2],lz[N<<2];
    void pd(int x){
        if(!lz[x]) return;
        c[ls]+=lz[x],c[rs]+=lz[x];
        f[ls]+=lz[x],f[rs]+=lz[x];
        lz[ls]+=lz[x],lz[rs]+=lz[x];
        lz[x]=0;
    }
    void pu(int x){
        f[x]=max(f[ls],f[rs]);
        c[x]=min(c[ls],c[rs]);
    }
    void bld(int x,int l,int r){
        if(l==r){
            f[x]=min(pre[l],suf[l]);
            c[x]=f[x]-a[l]; return;
        }
        bld(ls,l,mid),bld(rs,mid+1,r);
        pu(x);
    }
    void mdf(int x,int l,int r,int ql,int qr,int k){
        if(ql<=l&&r<=qr){
            c[x]+=k,f[x]+=k,lz[x]+=k;
            return;
        }
        pd(x);
        if(ql<=mid) mdf(ls,l,mid,ql,qr,k);
        if(mid<qr)  mdf(rs,mid+1,r,ql,qr,k);
        pu(x);
    }
    int get(int x,int l,int r,int ql,int qr){
        if(ql<=l&&r<=qr) return f[x];
        pd(x); int res=0;
        if(ql<=mid) res=max(res,get(ls,l,mid,ql,qr));
        if(mid<qr)  res=max(res,get(rs,mid+1,r,ql,qr));
        return res;
    }
    int chl(int x,int l,int r,int k){
        if(l==r) return f[x]==k?l:-1;
        pd(x);
        if(f[ls]==k) return chl(ls,l,mid,k);
        if(f[rs]==k) return chl(rs,mid+1,r,k);
        return -1;
    }
    int lmx(){return chl(1,1,n,f[1]);}
    int chr(int x,int l,int r,int k){
        if(l==r) return f[x]==k?l:-1;
        pd(x);
        if(f[rs]==k) return chr(rs,mid+1,r,k);
        if(f[ls]==k) return chr(ls,l,mid,k);
        return -1;
    }
    int rmx(){return chr(1,1,n,f[1]);}
    int gmn(int x,int l,int r,int ql,int qr){
        if(ql<=l&&r<=qr) return c[x];
        pd(x); int res=1e9;
        if(ql<=mid) res=min(res,gmn(ls,l,mid,ql,qr));
        if(mid<qr)  res=min(res,gmn(rs,mid+1,r,ql,qr));
        return res;
    }
    int gtl(int x,int l,int r,int ql,int qr){
        if(l==r) return l;
        pd(x);
        if(ql<=mid&&gmn(ls,l,mid,ql,mid)<=0) return gtl(ls,l,mid,ql,qr);
        if(mid<qr&&gmn(rs,mid+1,r,mid+1,qr)<=0) return gtl(rs,mid+1,r,ql,qr);
    }
    int gl(int x){return gtl(1,1,n,x+1,n);}
    int gtr(int x,int l,int r,int ql,int qr){
        if(l==r) return l;
        pd(x);
        if(mid<qr&&gmn(rs,mid+1,r,mid+1,qr)<=0) return gtr(rs,mid+1,r,ql,qr);
        if(ql<=mid&&gmn(ls,l,mid,ql,mid)<=0) return gtr(ls,l,mid,ql,qr);
    }
    int gr(int x){return gtr(1,1,n,1,x-1);}
    void test(){ cout<<"|";
        for(int i=1;i<=n;i++) cout<<get(1,1,n,i,i)<<" ";
        cout<<"\n";
    }
}; Misaka Mikoto;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin>>n; int q; cin>>q;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) pre[i]=max(pre[i-1],a[i]);
    for(int i=n;i>=1;i--) suf[i]=max(suf[i+1],a[i]);
    Mikoto.bld(1,1,n); //Mikoto.test();
    while(q--){
        int opt,x; cin>>opt>>x;
        if(opt==1){
            int S=Mikoto.rmx();
            if(x>=S) Mikoto.mdf(1,1,n,1,S,-1);
            else Mikoto.mdf(1,1,n,1,Mikoto.gl(x)-1,-1);
            //Mikoto.test();
        }
        else if(opt==2){
            int S=Mikoto.lmx(); x=n-x+1;
            if(x<=S) Mikoto.mdf(1,1,n,S,n,-1);
            else Mikoto.mdf(1,1,n,Mikoto.gr(x)+1,n,-1);
            //Mikoto.test();
        }
        else cout<<min(Mikoto.get(1,1,n,x,x),a[x])<<"\n";
    }
    return 0;
}

如果有更简便的解法，欢迎找我理性讨论。