莫比乌斯反演学习笔记—数论

前言： 作者初学数论，如有不足还请指出。

基本概念

定义

\[\mu(x)=\begin{cases} 1&n=1或n 无平方因子且质因子个数为偶数\\ 0&n 含有平方因子\\ -1&n 无平方因子且质因子个数为奇数 \end{cases} \]

核心性质

都挺巧妙的

1.莫⽐乌斯反演

\[\sum_{d|n}\mu(d)=[n=1] \]

证明:

• 首先 \(n=1\) 时显然是成立的
• 当 \(n>1\) 时，不妨设 \(n\) 有 \(p\) 个质因子，则有

\[\sum_{d|n}=\sum_{i=1}^p{p\choose k}(-1)^i\times 1^{(p-i)}=(-1+1)^p=0 \]

从实际意义上来说，考虑枚举产生贡献为 \(d\) 的个数，质因数个数为 \(i\) 的 贡献为 \(d\) 的个数为 \(p \choose i\)。

2.欧拉反演

\[\sum_{d|n}\phi(d)=n \]

证明:
首先有

\[n=\sum_{d|n}\sum_{i=1}^{n}{[gcd(i,n)=1]}=\sum_{d|n}\sum_{i=1}^{\frac{n}{i}}{[gcd(i,\frac{n}{d})=1]} \]

又有欧拉函数定义 \(\sum_{i=1}^{n}{[gcd(i,n)=1]=\phi(n)}\)
带入上式，得

\[n=\sum_{d|n}\phi(\frac{n}{d})=\sum_{d|n}\phi(d) \]

例题

先来几道简单的：

P3455 [POI 2007] ZAP-Queries & P2522 [HAOI2011] Problem b

P3455 [POI 2007] ZAP-Queries
P2522 [HAOI2011] Problem b

前一题是后一题的特殊情况双倍经验。
显然可以用前缀和算，转为求 \(\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)=k]\)。
接下来推式子：

\[\begin{aligned} &=\sum_{i=1}^{\lfloor{\frac{n}{k}}\rfloor}\sum_{j=1}^{\lfloor{\frac{m}{k}}\rfloor}[gcd(i,j)=1] (i,j\ 都除以\ k)\\ &=\sum_{i=1}^{\lfloor{\frac{n}{k}}\rfloor}\sum_{j=1}^{\lfloor{\frac{m}{k}}\rfloor}\sum_{d|gcd(i,j)}\mu(d) \end{aligned} \]

然后 \(d|gcd(i,j)\Longleftrightarrow d|i,d|j\)

\[\begin{aligned} &\sum_{d=1}^{min(\lfloor{\frac{n}{k}}\rfloor,\lfloor{\frac{m}{k}}\rfloor)}\mu(d)\sum_{i=1,i|d}^{\lfloor{\frac{n}{k}}\rfloor}\sum_{j=1,j|d}^{\lfloor{\frac{m}{k}}\rfloor}1\\ =&\sum_{d=1}^{min(\lfloor{\frac{n}{k}}\rfloor,\lfloor{\frac{m}{k}}\rfloor)}\mu(d)\lfloor\frac{\lfloor{\frac{n}{k}}\rfloor}{d}\rfloor\lfloor\frac{\lfloor{\frac{m}{k}}\rfloor}{d}\rfloor \end{aligned} \]

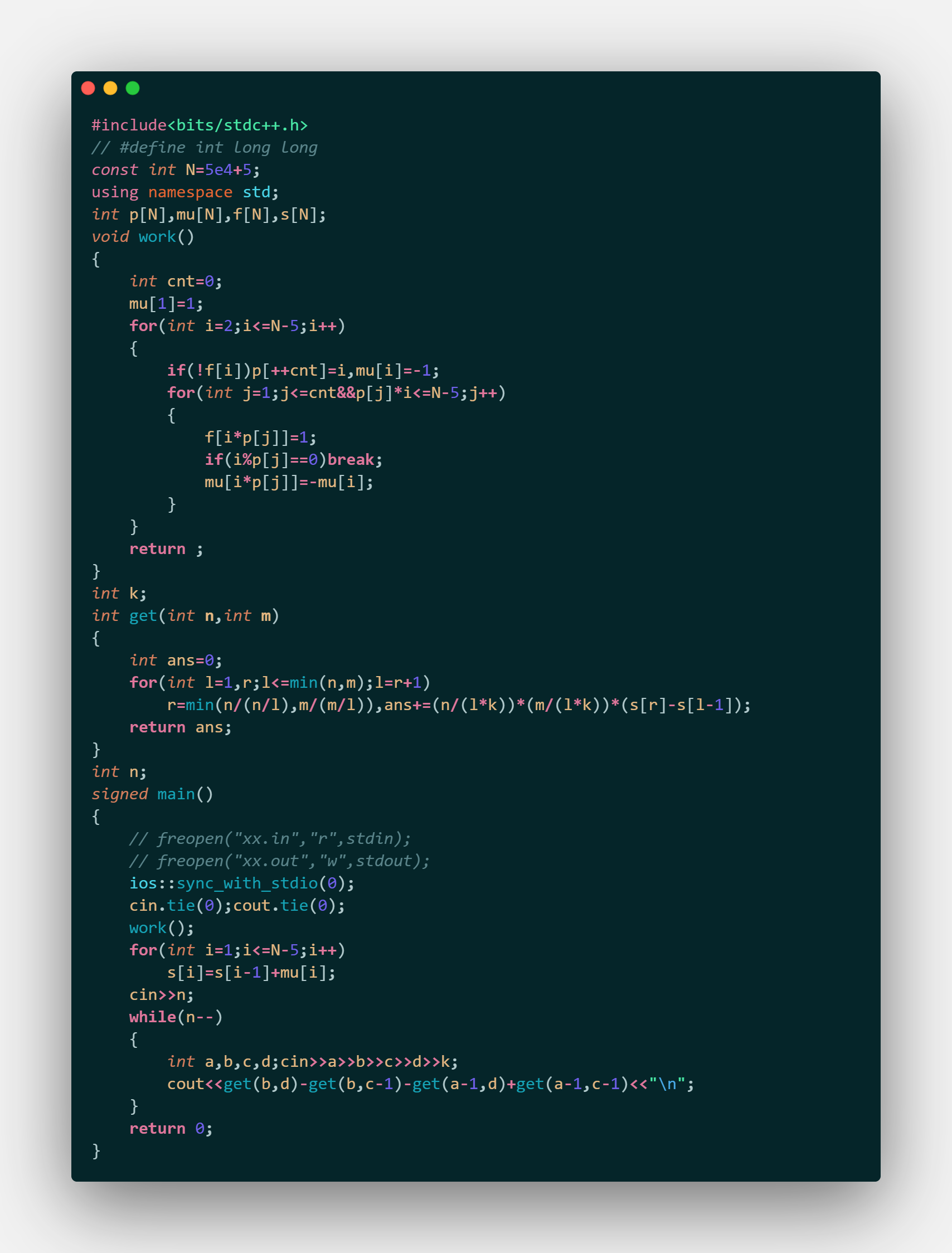
线性筛预处理莫比乌斯函数与前缀和 \(O(n)\)，每次询问数论分块 \(O(\sqrt{n})\)。

code
放 P2522 Problem B 的代码，另一题几乎相同。